二次插值法：手机壳制作中的高效模板制作技术

二次插值法又称为抛物线法，它是以目标函数的二次插值函数的极小点作为新的中间插入点，进行区间缩小的一维搜索算法。二次插值法的基本原理如下：

在一元函数的初始区间[a，b]内，取三个点：x₁=a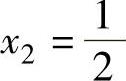，（a+b），x₃=b，计算函数值f₁=f（x₁），f₂=f（x₂），f₃=f（x₃）。在二维坐标平面内，过（x₁，f₁）、（x₂，f₂）和（x₃，f₃）三点可以构成一个二次插值函数。设该插值函数为

p（x）=a₀+a₁x+a₂x²

将该函数对x求导，得极小点

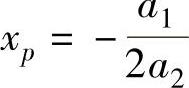
将区间内的三点及其函数值代入插值函数p（x），可以得到如下方程组

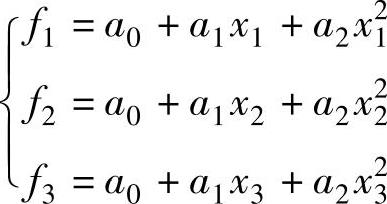
联立求解以上方程组，可得系数a₀、a₁和a₂，将它们代入插值函数p（x）并求得其极值

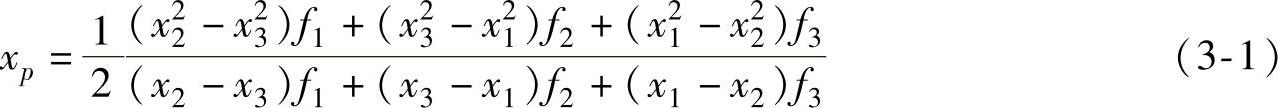
为了便于计算，可将上式改写成

式中

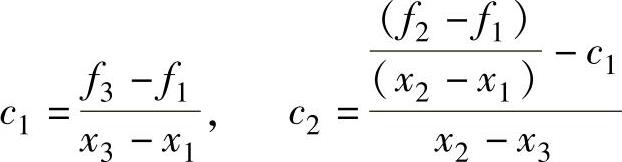
由式（3-2）求出的x_p是插值函数x_p的极小点，也是原目标函数的一个近似极小点。以此点作为下一次缩小区间的一个中间插入点，无疑将使新的插入点向极小点逼近的过程加快，如图3-7所示。

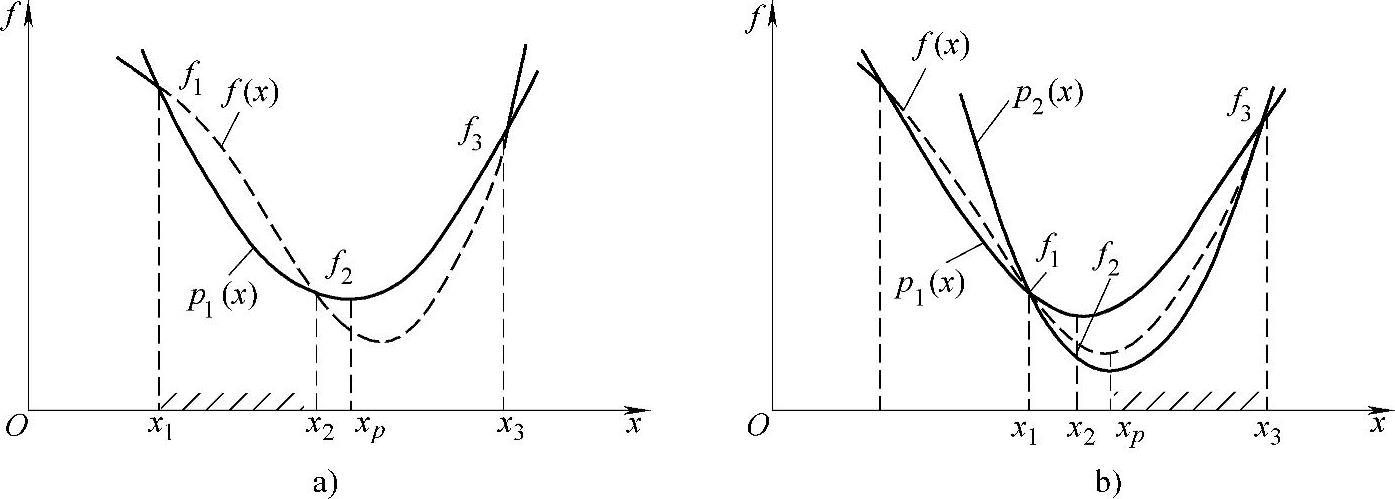
图3-7 二次插值法的区间缩小和逼近过程

需要指出的是，二次插值法每次插入的点比较接近函数的极小点，因此其收敛速度较黄金分割法快。二次插值法以两个中间插入点的距离充分小作为收敛准则，即当|x_p-x₂|≤ε成立时，把x_p作为此次一维搜索的极小点。

二次插值法的计算过程如下：

1）给定初始搜索区间[a，b]，收敛精度ε，以及区间的另外一个点c（一般情况下，取点）。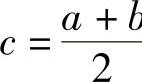

2）取x₁=a，x₂=c，x₃=b，分别求出f₁=f（x₁），f₂=f（x₂），f₃=f（x₃），构成三个插值点。

3）按照式（3-1）计算中间插入点x_p及其函数值f_p=f（x_p）。

4）缩短搜索区间。缩短搜索区间的原则是：比较f₂与f_p的大小，取其小者所对应的点作新的x₂点，并以此点左右邻点分别取作为新的x₁和x₃点，这样构成了缩短后的新搜索区间[x₁，x₃]。根据原区间中x₂与x_p、f₂与f_p的大小关系，区间缩短有四种情况，如图3-8所示，相应得到新的三个区间插入点。

①若f_p≤f₂，x_p≤x₂时，令x₃=x₂，x₂=x_p，f₃=f₂，f₂=f_p。

②若f_p≤f₂，x_p＞x₂时，令x₁=x₂，x₂=x_p，f₁=f₂，f₂=f_p。(www.xing528.com)

③若f_p＞f₂，x_p≤x₂时，令x₁=x_p，f₁=f_p。

④若f_p＞f₂，x_p＞x₂时，令x₃=x_p，f₃=f_p。

得到新的区间插入点以后，返回第三步进行插值计算。

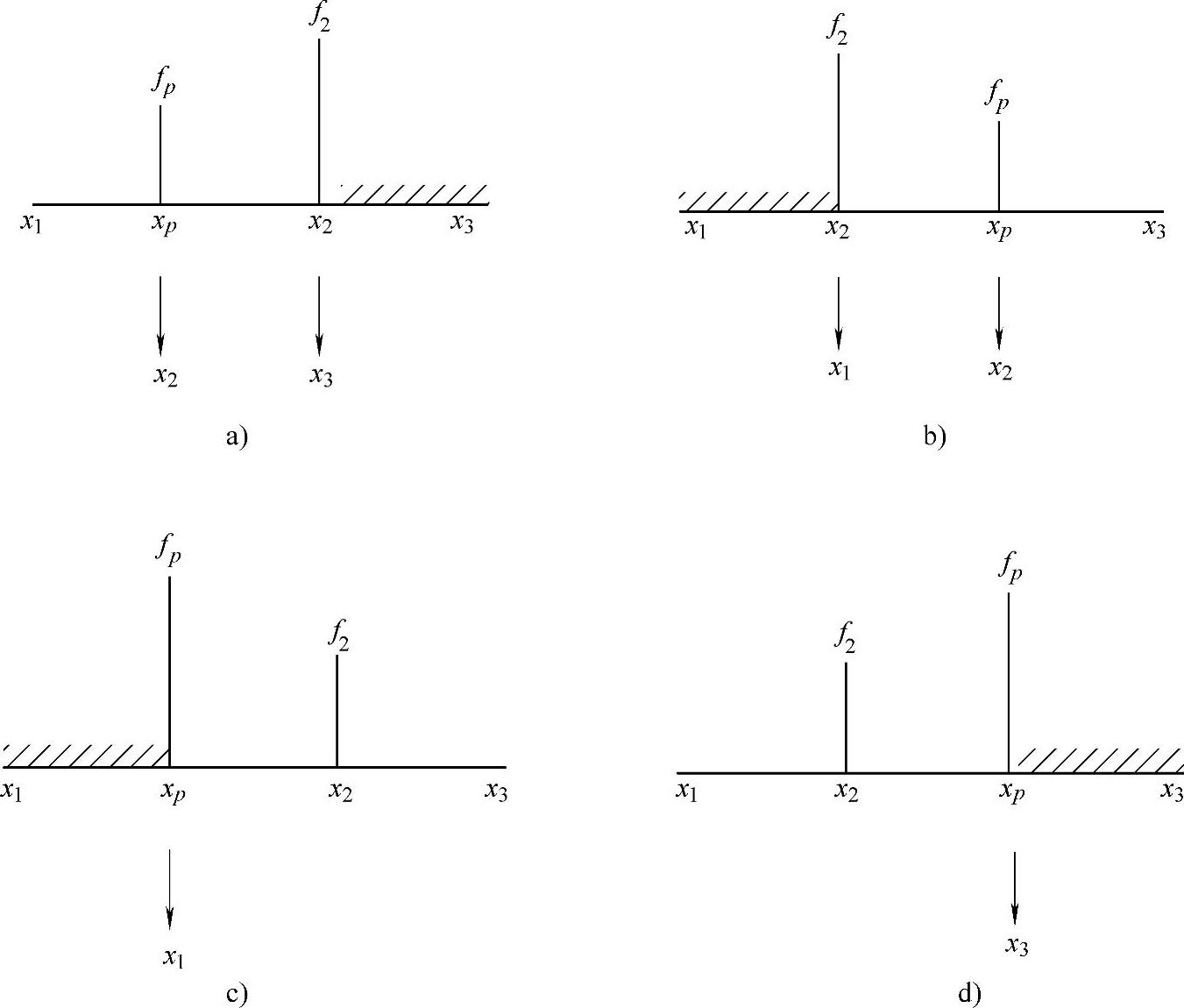
图3-8 二次插值法的区间取舍及替换

5）当满足|x_p-x₂|≤ε时，停止迭代，把x_p与x₂中原函数值较小的点作为极小点。二次插值法的计算框图如图3-9所示。

例3-2 用二次插值法求解例3-1。

解：1）根据例3-1可知，初始搜索区间为[0，2]，另外取一个中间点。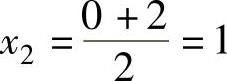

2）用二次插值法逼近极小点。

①根据x₁=0，x₂=1，x₃=2，求得f₁=2，f₂=1，f₃=18。将它们代入式（3-1）得

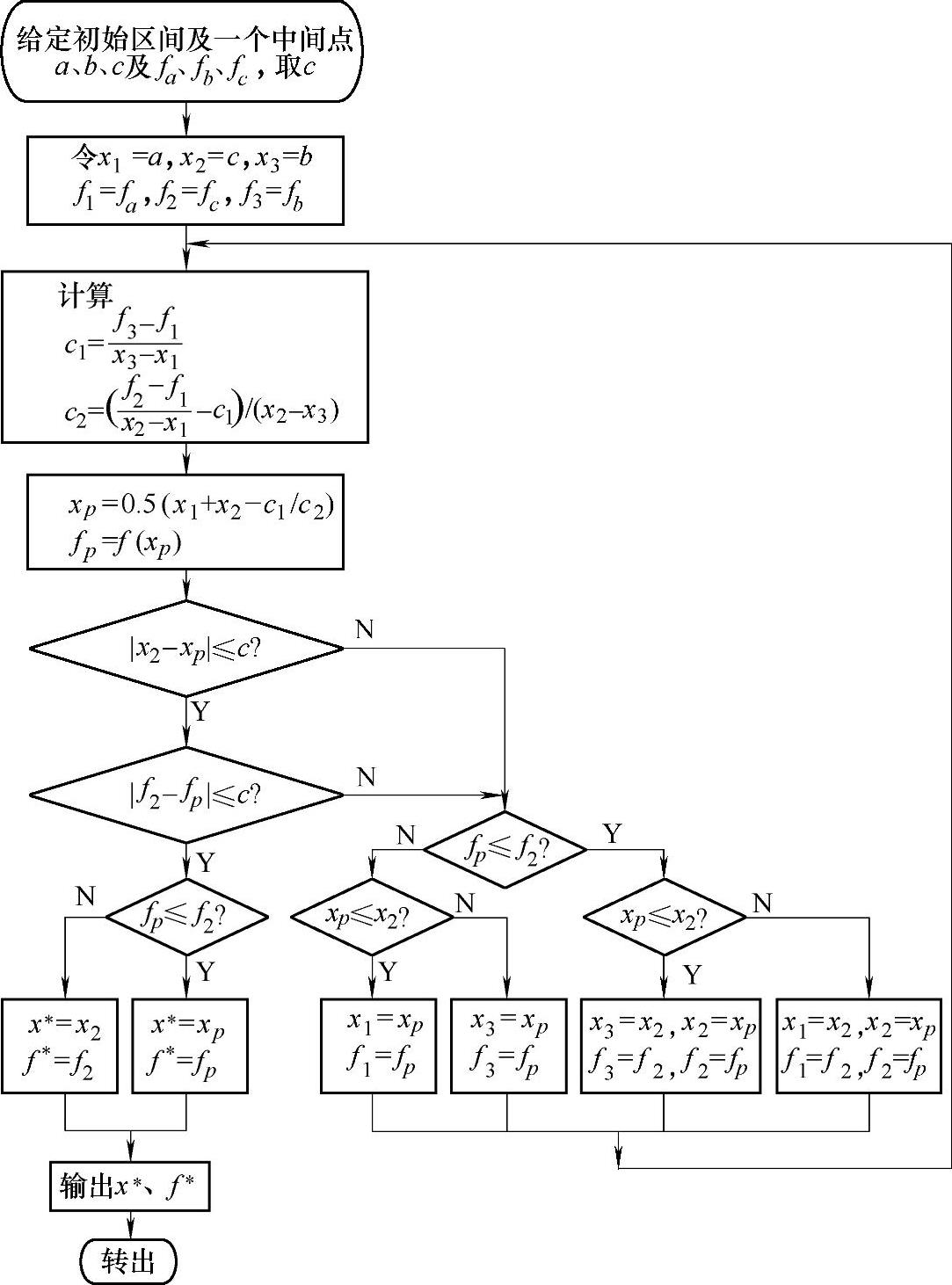
图3-9 二次插值法的计算框图

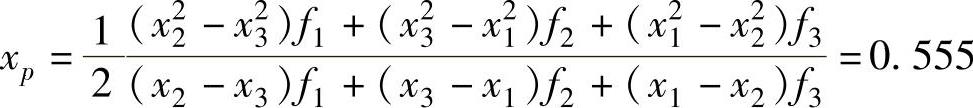
f_p=0.292

由于f_p＜f₂，x_p＜x₂，故新区间[a，b]=[a，x₂]=[0，1]。

由于x₂-x_p=1-0.555=0.445＞0.2，故应继续做第二次插值计算。

②在新的区间内，相邻三点及其函数值依次为：x₁=0，x₂=0.555，x₃=1，f₁=2，f₂=0.292，f₃=1。同样代入式（3-1）得

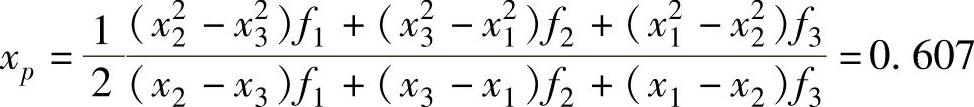
f_p=0.243

根据f_p＜f₂，x_p＞x₂，故新区间[a，b]=[x₂，b]=[0.555，1]。

由于x₂-x_p=0.555-0.607=0.052＜0.2，则迭代结束，得到的极小点和极小值分别为

x^∗=0.607，f^∗=0.243