有限元分析(Finite Element Analysis,FEA)的基本思想是用简单的问题代替复杂的问题后再求解。它将求解域看成是由许多称为有限元的小的相互连接域组成,对每个单元假定一个合适的近似解,然后推导求解这个域总的满足条件(如结构的平衡条件),从而得到问题的解。这个解是近似解,而不是准确的解。由于大多数实际问题难以得到准确的解,有限元分析不仅计算精度高,而且能适应各种复杂形状,因而成为行之有效的工程分析手段。
有限元法的基本思想是先将研究对象的连续求解域离散为一组有限个且按一定方式相互连接在一起的单元组合体。由于单元能按不同的连接方式进行组合,且单元本身又可以有不同的形状,因此可以模拟成不同几何形状的求解小区域;然后对单元进行力学分析,最后再整体分析。这种化整为零、集零为整的方法就是有限元的基本思路。
有限元法的形成可以回溯到20世纪50年代,来源于固体力学中矩阵结构法的发展和工程师对结构相似性的直觉判断。从固体力学的角度来看,桁架结构等标准离散系统与人为地分割成有限个分区后的连续系统在结构上存在相似性。
1956年M.J.Turner,R.W.Clough,H.C.Martin,L.J.Topp在纽约举行的航空学会年会上介绍了一种新的计算方法,将矩阵位移法推广到求解平面应力问题。他们把结构划分为一个三角形和矩形的“单元”,利用单元中近似位移函数,求得单元节点力与节点位移关系的单元刚度矩阵。
1954—1955年,J.H.Argyris在航空工程杂志上发表了一组能源原理和结构分析论文。
1960年,Cloud在他的名为“The finite element in plane stress analysis”的论文中首次提出了有限元(finite element)这一术语。
数学家们则发现了微分方程的近似解法,包括有限差分法、变分原理和加权余量法。
1963年前后,经过J.F.Besseling,R.J.Melosh,R.E.Jones,R.H.Gallaher,T.H.H.Pian等许多人的努力,人们认识到有限元法就是变分原理中里兹(Ritz)近似法的一种变形,发现了用各种不同变分原理导出的有限元计算公式。
1965年,O.C.Zienkiewicz和Y.K.Cheung(张佑启)发现只要能写成变分形式的所有场问题,都可以用与固体力学有限元法的相同步骤求解。(https://www.xing528.com)
1969年B.A.Szabo和G.C.Lee指出了可以用加权余量法,特别是Galerkin法,导出标准有限元过程来求解非结构问题。
我国的力学工作者为有限元方法的初期发展做出了许多贡献,其中比较著名的有:陈伯屏(结构矩阵方法),钱令希(余能原理),钱伟长(广义变分原理),胡海昌(广义变分原理),冯康(有限单元理论)。
有限元法不仅能应用于结构分析,还能解决可归结为场问题的工程问题。20世纪60年代中期以来,有限元法得到了巨大的发展,为工程设计和优化提供了有力的工具。人们通过大量的理论研究,拓展了有限元法的应用领域,发展了许多通用或专用的有限元分析软件。
理论研究的一个重要领域是计算方法的研究,主要有:大型线性方程组的解法、非线性问题的解法和动力问题的解法。
目前应用较多的通用有限元软件见表1-3。
表1-3 通用有限元软件
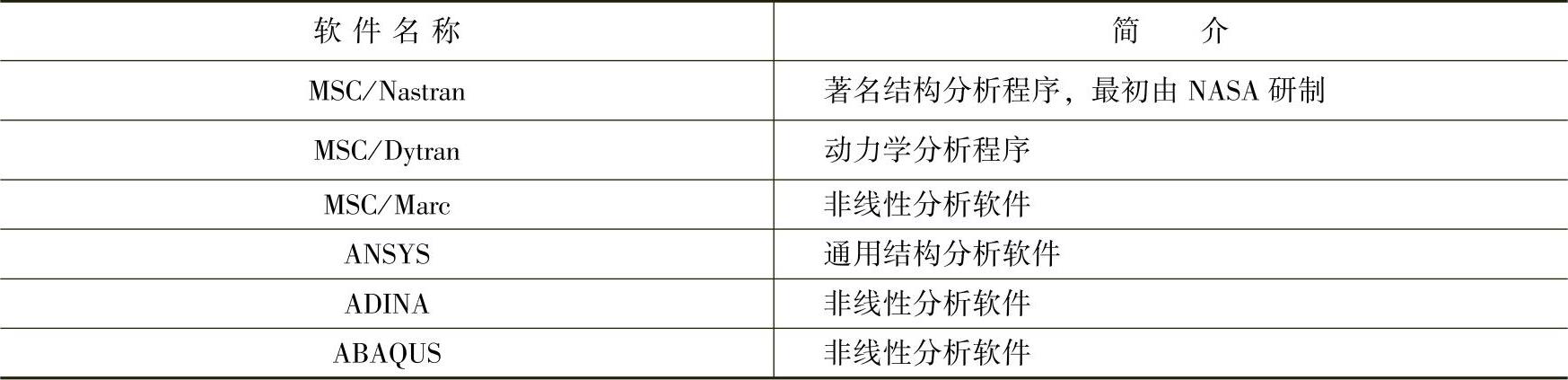
上述有限元软件均有各自的特点,但分析的基本理论和过程则大同小异。鉴于ANSYS作为一种应用广泛的有限元软件,后面章节中将以ANSYS的相关理论和操作进行介绍。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




