尺寸链中的基本术语：组成环、增环和补偿环

（1）尺寸链

在零件加工或机器装配过程中，由相互连接的尺寸形成封闭的尺寸组，称为尺寸链。

图12-1为齿轮部件各零件尺寸所形成的尺寸链。图12-2为托架位置尺寸（包括平行度、垂直度）形成的尺寸链。

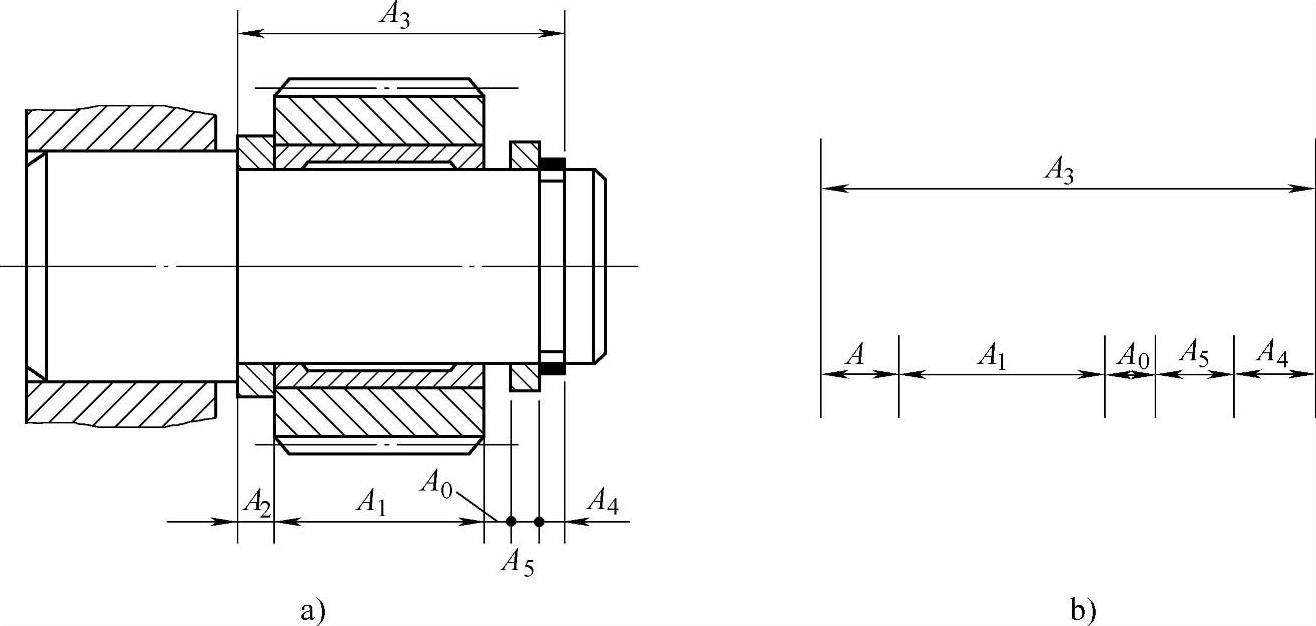
图12-1 齿轮部件的尺寸链

（2）环

列入尺寸链中的每一个尺寸称为环。图12-1中的A₁、A₂、…、A₅，图12-2中a₀、a₁、a₂都是环。

（3）封闭环

尺寸链在加工过程或装配过程最后自然形成的一环，称为封闭环。封闭环代号用加下角标“0”表示。

图12-1中的A₀、图12-2中的α₀为封闭环。

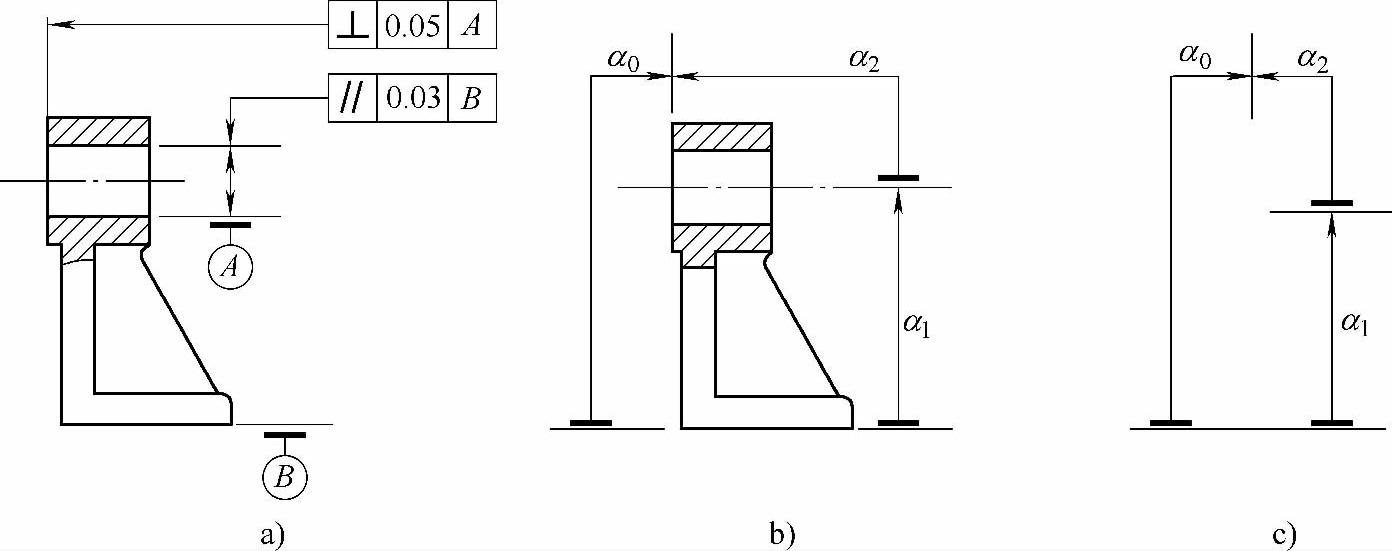
图12-2 托架位置尺寸链

（4）组成环

在尺寸链中对封闭环有影响的全部环，称为组成环。这些环中任一环的变动必然引起封闭环的变动，按其影响的不同，分为增环、减环和补偿环。图12-1中A₁、A₂、A₃、A₄、A₅及图12-2中α₁、α₂都是组成环。组成环代号用加下角标阿拉伯数字表示。

1）增环 在尺寸链的组成环中，由于该环的变动而引起封闭环的同向变动，则该类环称为增环。所谓同向变动是指该组成环增大时封闭环增大，该组成环减小时封闭环也减小。

图12-1中A₃是增环。(www.xing528.com)

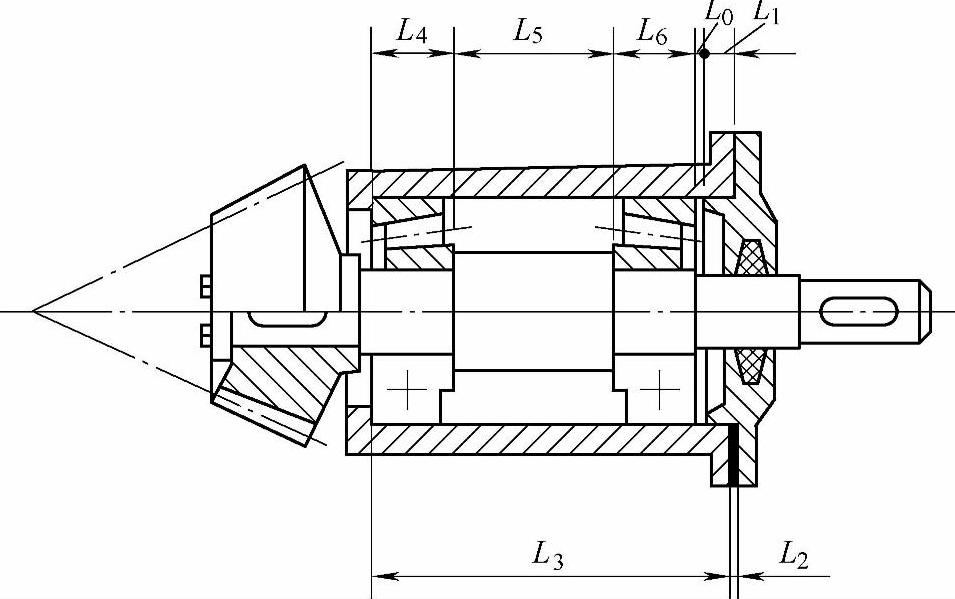
图12-3 补偿环

2）减环 在尺寸链的组成环中，由于该环的变动引起封闭环的反向变动，则该类组成环称为减环。所谓反向变动是指该组成环增大时封闭环减小，该组成环减小时封闭环增大。

图12-1中A₁、A₂、A₃、A₄、A₅和图12-2中α₁、α₂都为减环。

3）补偿环 在尺寸链中预先选定的某一组成环，可以改变其大小或位置，使封闭环达到规定要求，该组成环称为补偿环，如图12-3中的L₂。

（5）传递系数

表示各组成环对封闭环影响大小的系数称为传递系数。传递系数值等于组成环在封闭环上引起的变动量对该组成环本身变动量之比。

设L₁、L₂、…、L_m为各组成环，L₀为封闭环，则有

L₀=f（L₁、L₂、…、L_m）

式中，m为组成环的环数。

如图12-1和图12-2所示的尺寸链，则有

A₀=A₃-（A₁+A₂+A₄+A₅）和α₀=-（α₁+α₂）

假设第i组成环的传递系数为ξ_i，则

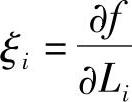
对于增环，ξ_i为正值；对于减环，ξ_i为负值。