化简带有无关项的逻辑函数

1. 约束概念和约束条件

在分析某些具体的逻辑函数时，经常会遇到这样一种情况，即输入变量的取值不是任意的。对输入变量取值所加的限制称为约束。同时，把这一组变量称为具有约束的一组变量，而不会出现的变量取值所对应的最小项叫作约束项。把恒等于0的约束项加起来所构成的值为0的逻辑表达式，叫作约束条件。因为约束项恒为0，而无论多少个0加起来还是0，所以约束条件是一个值恒为0的条件等式。

有时还会遇到另外一种情况，就是在输入变量的某些取值下函数值是1还是0皆可，并不影响电路的功能。在这些变量取值下，其值等于1的那些最小项称为任意项。

把约束项和任意项统称为逻辑函数式中的无关项。这里所说的“无关”是指是否把这些最小项写入逻辑函数式无关紧要，可以写入也可以删除。

2. 具有无关项的逻辑函数的化简

前面曾经讲到，在用卡诺图表示逻辑函数时，首先将函数化为最小项之和的形式，然后在卡诺图中这些最小项对应的位置上填“1”，在其他位置上填“0”。既然可以认为无关项包含在函数式中，也可以认为不包含在函数式中，那么在卡诺图中对应的位置上就可以填“1”，也可以填“0”。为此，在卡诺图中用 × 、d或φ表示无关项，在表达式中常用∑d来表示无关项最小项组合部分。在化简逻辑函数时既可以认为它是1，也可以认为它是0。

化简具有无关项的逻辑函数时，如果能合理利用这些无关项，一般都可得到更加简单的化简结果。

为了达到此目的，加入的无关项应与函数式中尽可能多的最小项（包括原有的最小项和已写入的无关项）具有逻辑相邻性。(www.xing528.com)

合并最小项时，究竟把卡诺图上的“ × ”作为1（即认为函数式中包含了这个最小项）还是作为0（即认为函数式中不包含这个最小项）对待，应以得到的相邻最小项矩形组合最大且矩形组合数目最少为原则。

例4 - 17 化简具有约束的逻辑函数：

解 先将表示Y的卡诺图画出，从图上直观地判断对这些约束项应如何取舍。如图4 - 19所示，为了得到最大的相邻最小项的矩形组合，应取约束项m3、m5为1，与m1、m7组成一个矩形组。同时取约束项m10、m12、m14为1，与m8组成一个矩形组。卡诺图中没有被圈进去的约束项（m9和m15）被当作0对待。

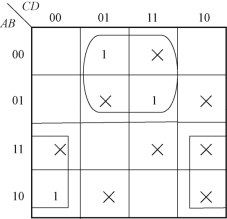
图4-19　例4-17的卡诺图

将两组相邻的最小项合并后得到：