化简逻辑函数的方法与技巧

对于一个逻辑函数来说，如果其逻辑表达式比较简单，那么实现这个逻辑表达所需的元器件较少，电路的可靠性也比较高。因此，经常需要通过化简的手段找出逻辑函数的最简形式。

1. 逻辑函数的最简表达式

一个逻辑函数的最简表达式，按照式中变量之间运算关系不同，主要分为最简与或式、最简或与式、最简与非式、最简或非式、最简与或非式5种，其中前两种用得最多。利用逻辑代数的基本定律，可以实现表达式之间的互换。

2. 公式化简法

化简逻辑函数的目的就是消去多余的乘积项和每个乘积项中多余的因子，得到逻辑函数式的最简因子。常见的有公式化简法和卡诺图化简法。

公式化简法的原理就是反复使用逻辑代数的基本定律和常用公式消去函数式中多余的乘积项和多余的因子，以求得函数的最简表达式。

公式化简法没有固定的步骤，现将经常使用的方法归纳如下。

1） 并项法

例4 - 8 用并项法化简下列逻辑函数:

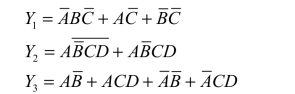
解

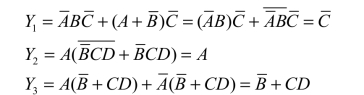
2） 吸收法

(www.xing528.com)

例4 - 9 用吸收法化简下列逻辑函数：

解

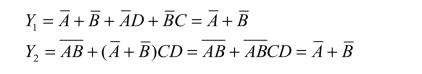
3） 消去法

例4 - 10 用消去法化简下列逻辑函数：

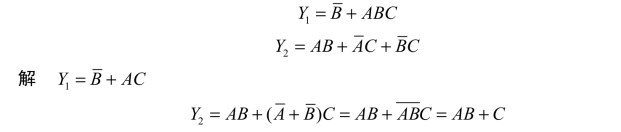
4） 配项法

根据A+A=A，可以在逻辑函数式中重复写入某一项，有时能获得更加简单的化简结果。

解 利用配项法可将Y写成：

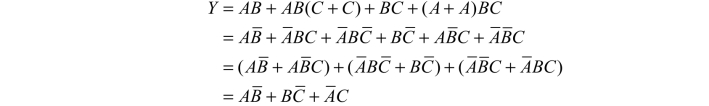
5） 配多余项法

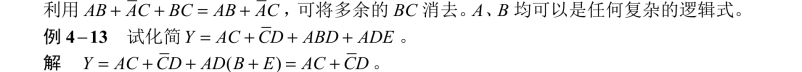
总而言之，在化简复杂的逻辑函数时，往往需要灵活、交替地综合运用上述方法，才能得到最后的化简结果，且逻辑函数的化简结果不是唯一的。