【摘要】：例4 - 1 将下列数字转换为相应的十进制数。表7-29 基准面与安装面的形状公差例4 - 3 将十进制小数10转换成二进制数。
任意进制数转换为十进制数只需按权展开，加权即可。
例4 - 1 将下列数字转换为相应的十进制数。
（1） (101.01)2；（2）(137.504)8；（3）(2AF.4)16。
解 按权展开，系数为0可忽略。
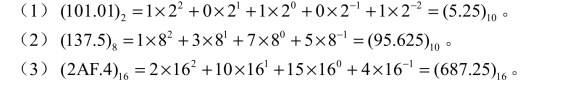
2. 十进制数转换为任意进制数
将十进制数转换为R进制数，需将十进制数的整数部分和小数部分分别进行转换，然后将它们合起来。
方法：逐次除以基数R取余数。步骤如下：
（1） 将给定的十进制整数除以R，余数作为R进制数的最低位。
（2） 把前一步的商除以R，余数作为次低位。
（3） 重复上一步骤，记下余数，直至最后商为0，最后的余数即R进制的最高位。
（4） 将小数部分逐次乘以R，取乘积的整数部分作为R进制数各有关数位。
（5） 乘积的小数部分继续乘以R，直至最后乘积为0或达到一定精度。
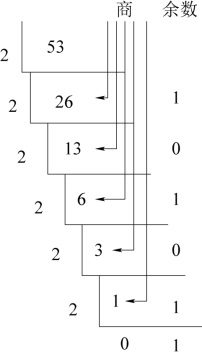
例4 - 2 将十进制数(53)10转换为二进制数。
解 (53)10=(110101)2。计算步骤如下：(www.xing528.com)
例4 - 3 将十进制小数(0.375)10转换成二进制数。
解 (0.375)10=(0.011)2。计算步骤如下（直到乘积为0或达到一定精度）：
将一个带有整数和小数的十进制数转换成R进制数时，需将整数部分和小数部分分别进行转换，然后将结果合并起来。因此有：
3. 二 - 八转换
基数R为2k的各进制数之间相互转换时，3位二进制数构成1位八进制数，4位二进制数构成1位十六进制数。例如：
4. 二 - 十六转换
如前所述，4位二进制数构成1位十六进制数。例如：
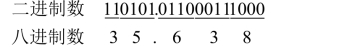
5. 八 - 十六转换
八进制数和十六进制数之间转换时，需要先转换为二进制数。例如：
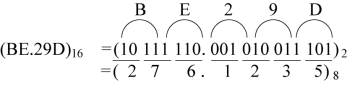
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
