常见数制：十进制、二进制、八进制、十六进制

1. 十进制

十进制是日常生活中使用最广泛的计数制。组成十进制数的有0、1、2、3、4、5、6、7、8、9共10个符号，称这些符号为数码。在十进制中，每一位有0～9共10个数码，所以计数的基数为10。超过9就必须用多位数来表示。十进制数的运算遵循加法时“逢十进一”、减法时“借一当十”的原则。

十进制数中，数码的位置不同，所表示的值就不相同。如：

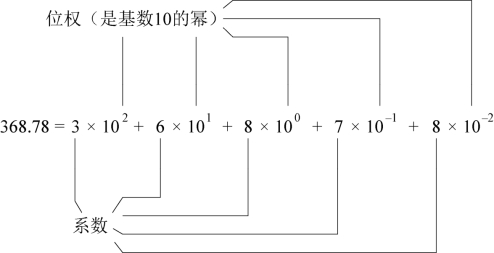
式中，每个对应的数码有一个系数1 000、100、10、1与之对应，这个系数叫作权或位权。

任意十进制数可表示为

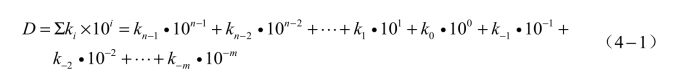
式中，ki为0～9中的任意数码；10为进制的基数；10i为第i位的权；m和n为正整数，n为整数部分的位数，m为小数部分的位数。

若以N取代式（4 - 1）中的10，即可得到多位任意进制（N进制）数展开式的普遍形式：

式中i的取值与式（4 - 1）的规定相同。N称为计数的基数，ki为第i位的系数，Ni称为第i位的权。

2. 二进制

十进制数在计算机中无法使用，因为要找到表达10个状态的物理元件比较困难，要完成十进制的加、减、乘、除运算也比较复杂。所以，数字电路（通信）和计算机中常用二进制数，及相应变形的八/十六进制数。

在二进制数中，每一位仅有0和1两个可能的数码，所以计数基数为2。低位和相邻高位间的进位关系为“逢二进一”。

根据式（4 - 2），任何一个二进制数均可展开为

并可用上式计算出它所表示的十进制数的大小。例如

(www.xing528.com)

上式中分别使用下脚注“2”和“10”表示括号里的数是二进制数和十进制数。有时也用B（Binary）和D（Decimal）代替“2”和“10”这两个下脚注。

3. 八进制

在某些场合有时也使用八进制数。八进制数的每一位有0～7共8个不同的数码，计数的基数为8。低位和相邻高位间的进位关系为“逢八进一”。任意一个八进制数均可展开为

也可用上式计算出它所表示的十进制数的大小，例如：

有时也用O（Octal）代替下脚注“8”，表示八进制数。

4. 十六进制

十六进制数的每一位有16个不同的数码，分别用0～9、A（10）、B（11）、C（12）、D（13）、E（14）、F（15）表示，故任意一个十六进制数均可展开为

并可用上式计算出它所表示的十进制数的大小，例如：

式中使用下脚注“16”表示括号里的数是十六进制数。有时也用H（Hexadecimal）代替下脚注“16”。

由于目前在微型计算机中普遍采用8位、16位和32位二进制数进行运算，而8位、16位和32位的二进制数可以用2位、4位和8位的十六进制数表示，因而十六进制符号书写程序十分简便。

表4 - 1所示为十进制数0～15与等值二进制数、八进制数、十六进制数的对照。

表4-1　不同进制数的对照