【摘要】:本节介绍的三要素法是一种求解一阶电路的简便方法,它可用于求解电路任一变量的零输入响应和直流作用下的零状态响应、全响应,不论它是状态变量还是非状态变量。则对于任意一阶微分方程,当它输入电源为稳定激励(直流)时,任意电压、电流响应的形式可表示为将此公式称为三要素公式。在外齿轮实际测量时,按规定作出的两内侧平行平面就是度量表面,以测量它们之间的距离。
本节介绍的三要素法是一种求解一阶电路的简便方法,它可用于求解电路任一变量的零输入响应和直流作用下的零状态响应、全响应,不论它是状态变量还是非状态变量。
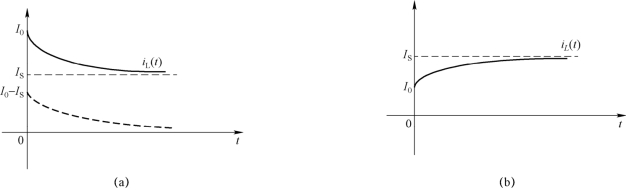
图3-5 不同情况下电感电流的变化曲线
(a)I0>IS;(b)I0<IS
这一方法的背景是:① 一阶电路中的响应是按指数规律变化的,都有它的初始值和稳态值(平衡值),其变化过程唯一地由时间常数决定;② “提前”运用换路定则,不必等状态变量求得后再运用。
考察一下全响应解的特点,以一阶RL电路为例。当换路发生在t = 0时刻,那么电流的全响应为
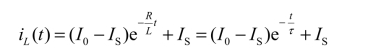
其中I0为电感电流的初始值iL(0+);IS是t→∞时的电流值,iL(∞)是稳态值;τ为时间常数。
在RC或RL电路中,不管电路结构和参数如何,换路后,描述电路特性与激励关系的方程为一阶微分方程,其数学模型为
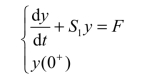
则对于任意一阶微分方程,当它输入电源为稳定激励(直流)时,任意电压、电流响应的形式可表示为
![]()
将此公式称为三要素公式。其中y(t)可以代表电路中的任一电压或电流;y(0+)表示该电压或电流的初始值;y(∞)表示该电压或电流的稳态值;τ表示电路的时间常数。只要知道y(0+)、τ、y(∞)即可,而它们均可不用列微分方程求得。
例3 - 3 电路如图3 - 6所示,求u C (t)、iC (t)、i1(t)。(https://www.xing528.com)
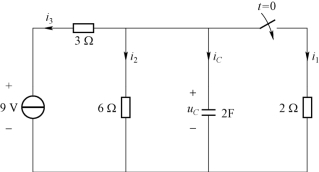
图3-6 例3-3图
解 t=0-时,开关处于断开状态,电容C相当于开路。
(1)求初值。
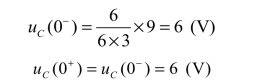
(2)求终值。t→∞时,电路将再次进入稳态。
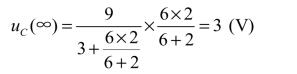
(3)求时间常数。把电容C开路,并将电压源短路,R为从电容向外看的等效电阻:
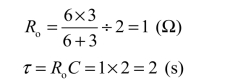
代入三要素公式:
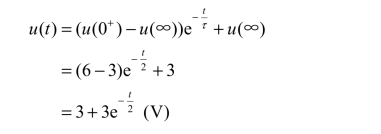
求其他电量:
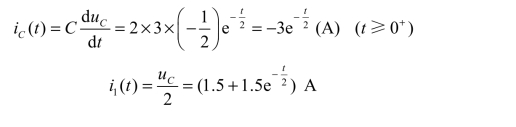
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




