如何实现尺寸公差统计与规范化？

指导性文件JB/Z 304—1987《统计尺寸公差》^[1]主要用于长度尺寸。在选择或计算公差与配合时，一般是不考虑实际尺寸的概率分布的，而这一因素对相关尺寸间的关系的影响，有时是不可忽略的，考虑实际尺寸的概率分布，采用统计尺寸公差，可使产品获得较佳的技术经济效果。如孔、轴实际尺寸的概率分布对孔、轴配合的性能具有很大的影响，孔、轴采用统计公差可以获得如下效果：

可以保证过渡配合的确定性；可更多地获得具有最佳“间隙或过盈”的配合；减少装配时孔、轴极限尺寸相逢的概率；提高零部件的磨损储备与强度储备等。

（1）主要术语（图1-33和表1-49）

（2）规定实际尺寸概率分布特性的方案

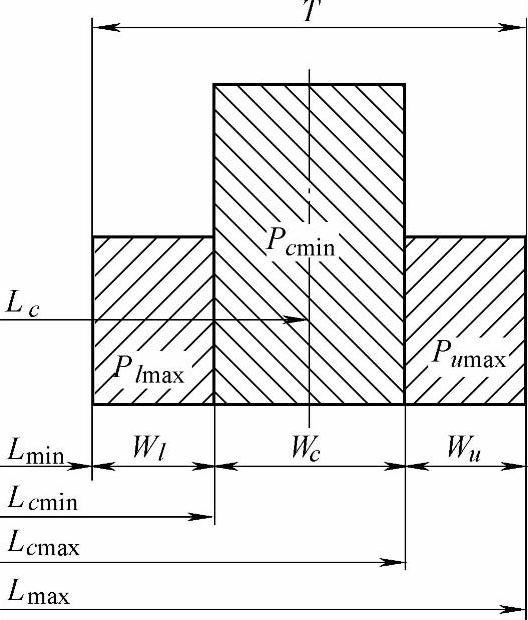
图1-33 统计尺寸图解

标准规定可用a、b、c三种方案之一对实际尺寸概率分布特性作出规定，方案见表1-50。

表1-49 统计尺寸公差术语

（续）

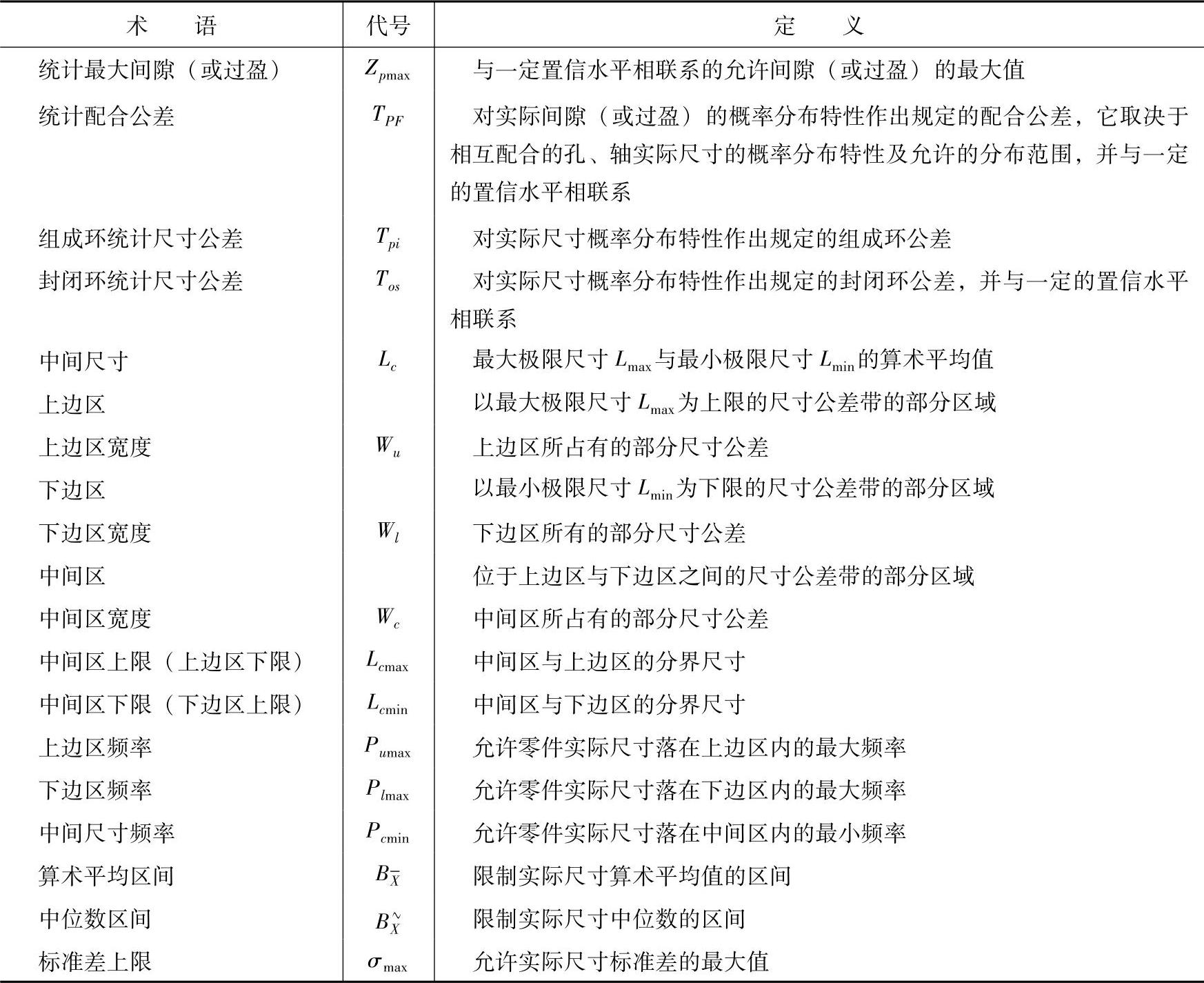
表1-50 实际尺寸概率分布特性的规定方案

（3）统计尺寸公差在图样上的标注

按上述三方案标注示例如下：

1）按方案a标注

55±0.06±0.03P86%

式中 55——公称尺寸（mm）；

（55+0.06）——最大极限尺寸（mm）；

（55-0.06）——最小极限尺寸（mm）；

P86%——表示P_cmin等于86%，即在中间区（55±0.03）mm范围内至少有86%的零件。

无特别说明时则

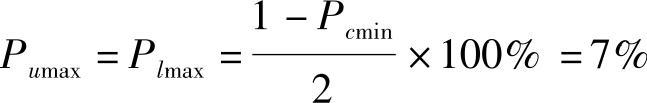
即在上边区（55^+0.06_+0.03）mm或下边区（55^-0.03_-0.06）mm范围内最多包含有7%的零件。

2）按b方案标注

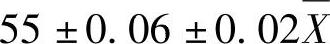
表示实际尺寸的算术平均必须位于（55±0.02）mm的区间内。

如需要规定σ_max时，可加注在括号内，即

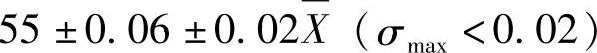
3）按c方案标注

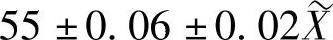
表示实际尺寸的中位数必须位于（55±0.02）mm的区间内。

如需要规定σ_max时，可加注在括号内，即

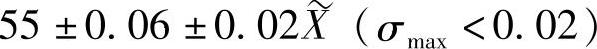
4）简化标注

当采用简化标注时，对统计尺寸公差的具体要求应在技术条件中具体说明，或由技术文件统一规定。简化标注示例见图1-34。

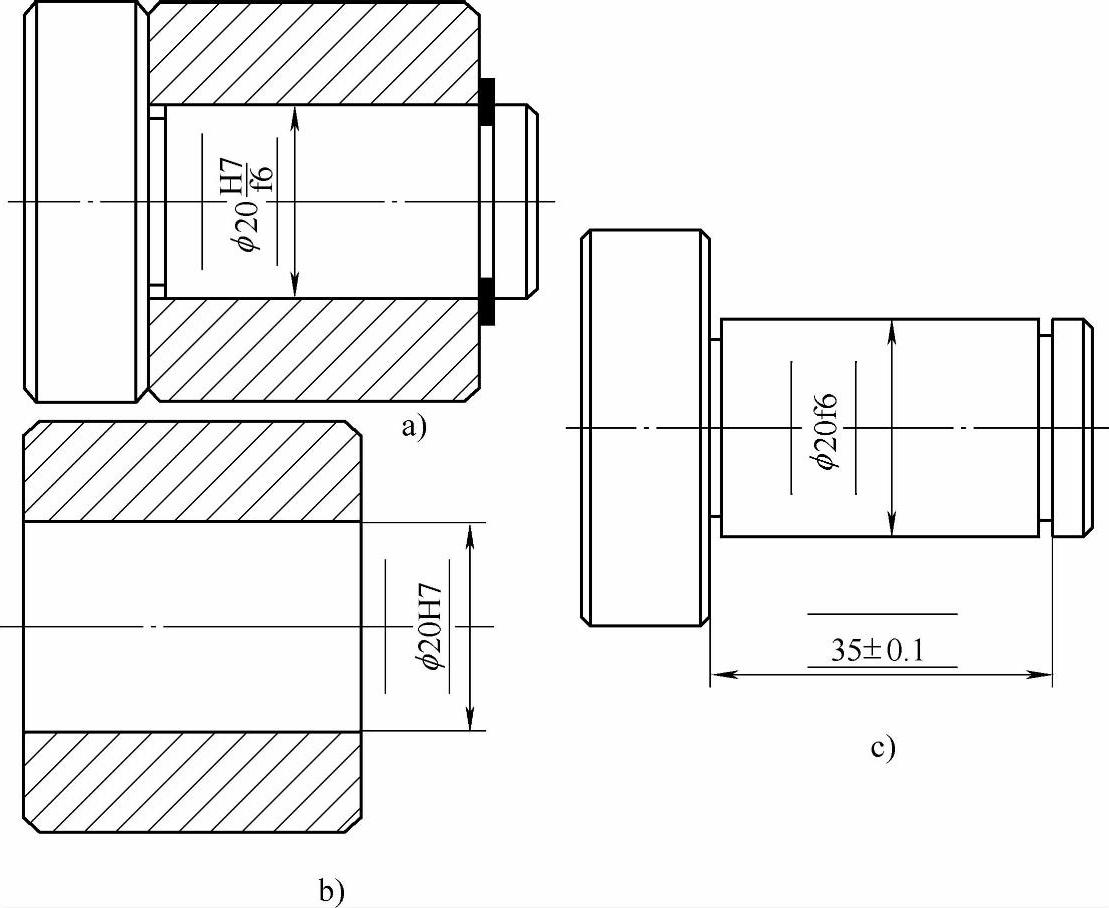
图1-34 统计尺寸公差简化标注示例

（4）统计尺寸公差在孔、轴配合中的应用

1）对孔、轴实际尺寸概率分布特性要求的规定

a）公差带的划分

对于对称分布，推荐

T∶W_c=2∶1

对于非对称分布，三个区域的划分可根据实际情况决定。

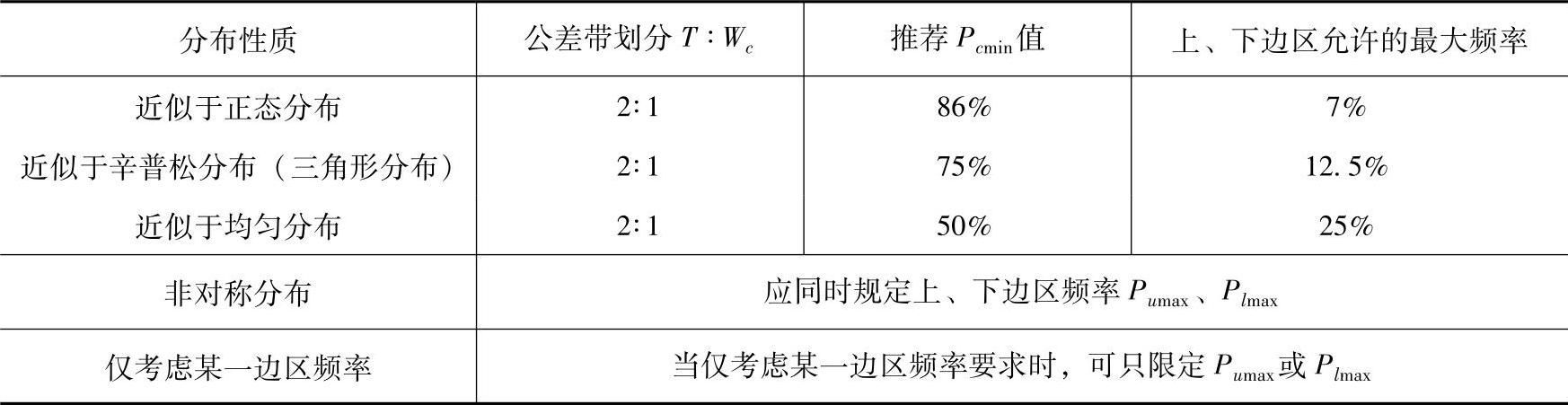
b）频率的决定（表1-51）

表1-51 频率的决定

c）标注举例

对于对称分布，如

φ55±0.06±0.03P86%

表示上、下边区的频率均不超过7%。

对于非对称分布，如

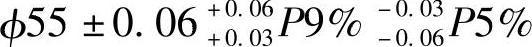
表示上边区频率不超过9%，下边区频率不超过5%。

仅规定某一边区的频率，如

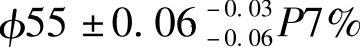
表示仅对下边区有频率要求，且不超过7%。

2）统计配合公差的简化计算

在应用中，根据孔、轴公差T_H、T_S及其实际尺寸的概率分布特性和分布范围，并给出一定置信水平，可用简化公式计算出统计配合公差T_PF、统计最小间隙（或过盈）Z_pmin及统计最大间隙（或过盈）Z_pmax。

a）孔轴实际尺寸趋近正态分布时，若

T∶W_c=2∶1，P_cmin=86%

则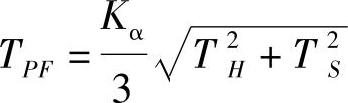

取置信水平1-α=99.73%时，在有关概率与数理统计手册中可查得

K_α=3

并有配合公差

T_F=T_H+T_S(www.xing528.com)

当孔、轴公差等级相等，即T_H=T_S，则

T_PF=0.71T_F当孔比轴公差低一级，即T_H=1.6T_S，则

T_PF=0.73T_F

b）孔、轴实际尺寸趋近辛普松分布时，若

T∶W_c=2∶1，P_cmin=75%

则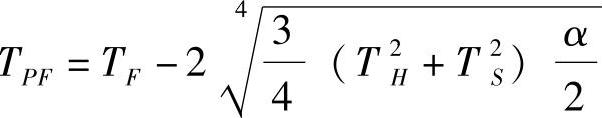

当T_H=T_S，且1-α=99.73%时，则

T_PF=0.79T_F

c）孔轴实际尺寸趋近均匀分布时，若

T∶W_c=2∶1，P_cmin=50%

则

当T_H=T_S，且1-α=99.73%时，则

T_PF=0.95T_F

d）统计极限间隙（或过盈）

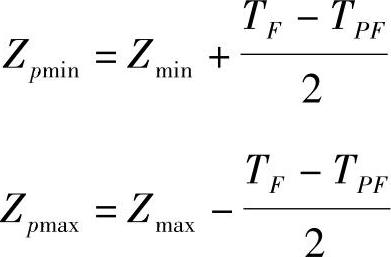
式中，Z_min、Z_max相应为配合最小、最大间隙或过盈。

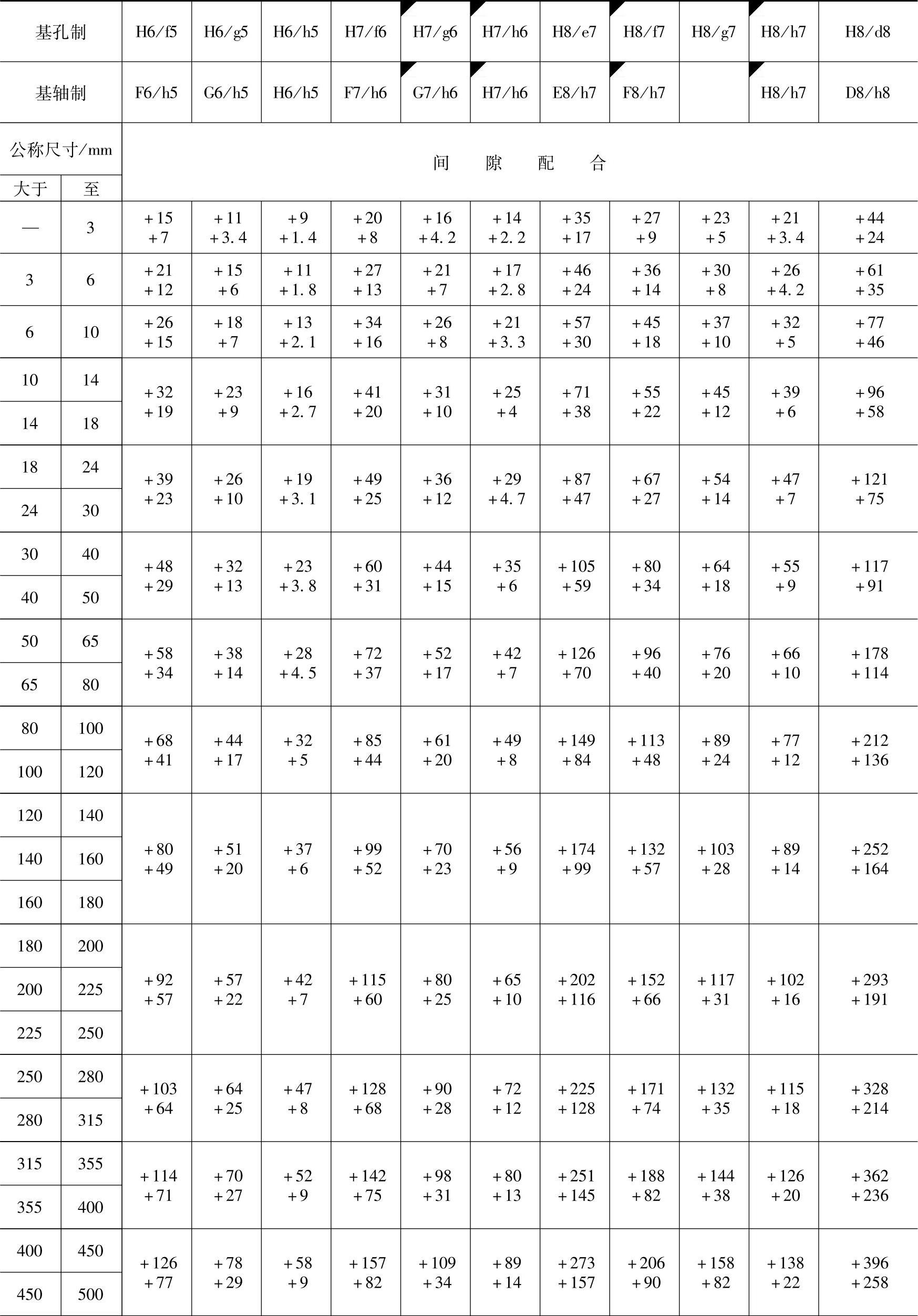
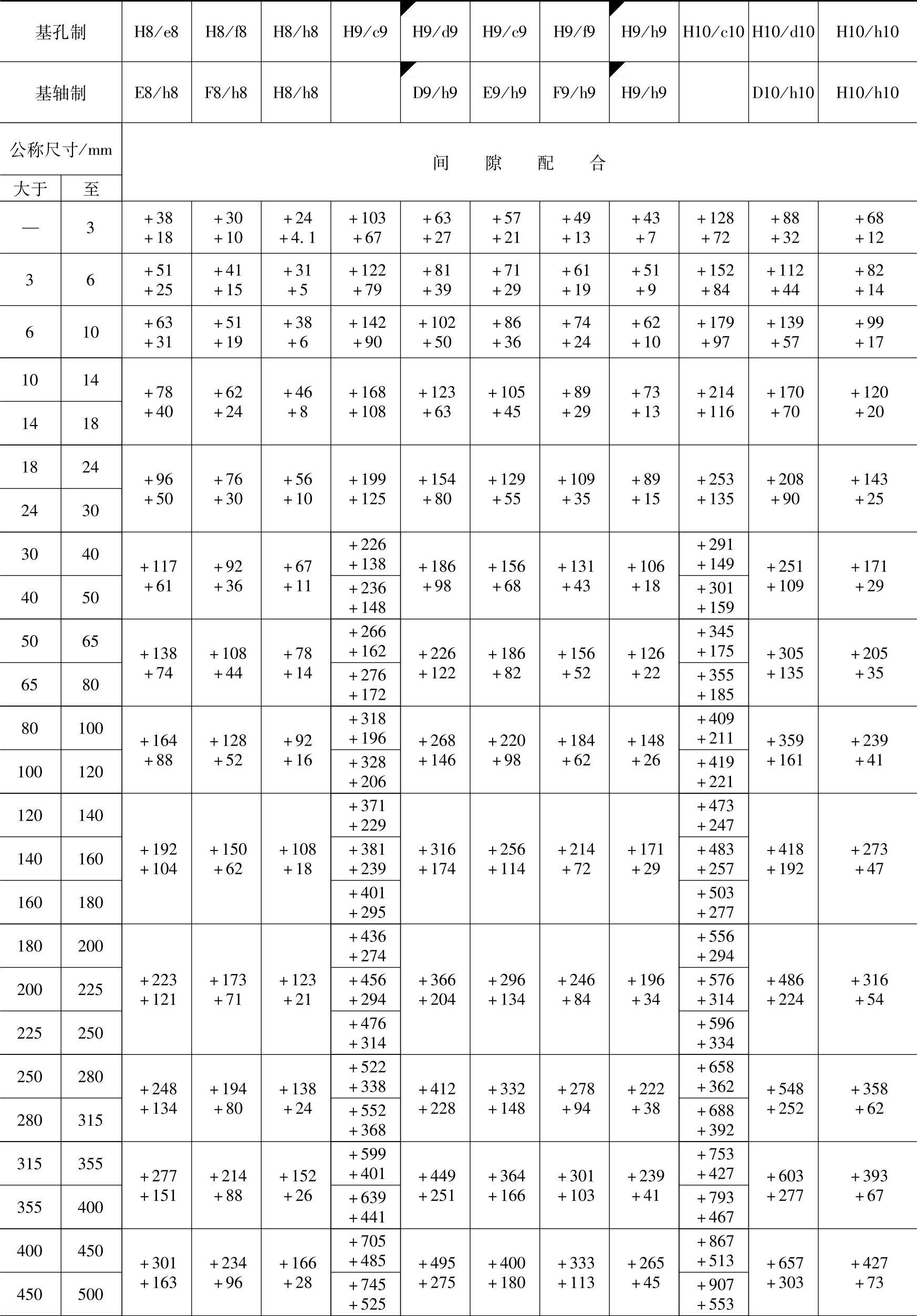
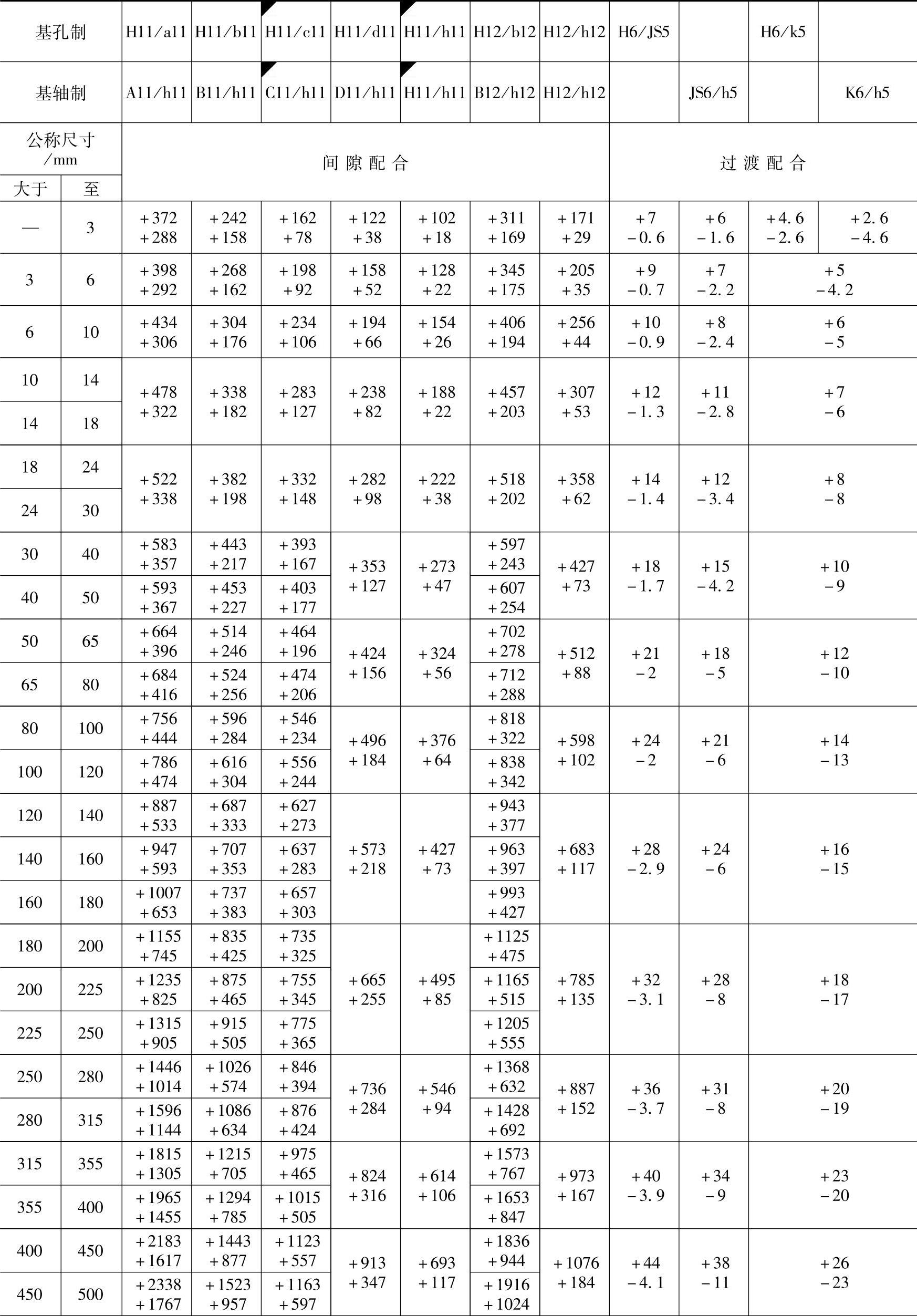
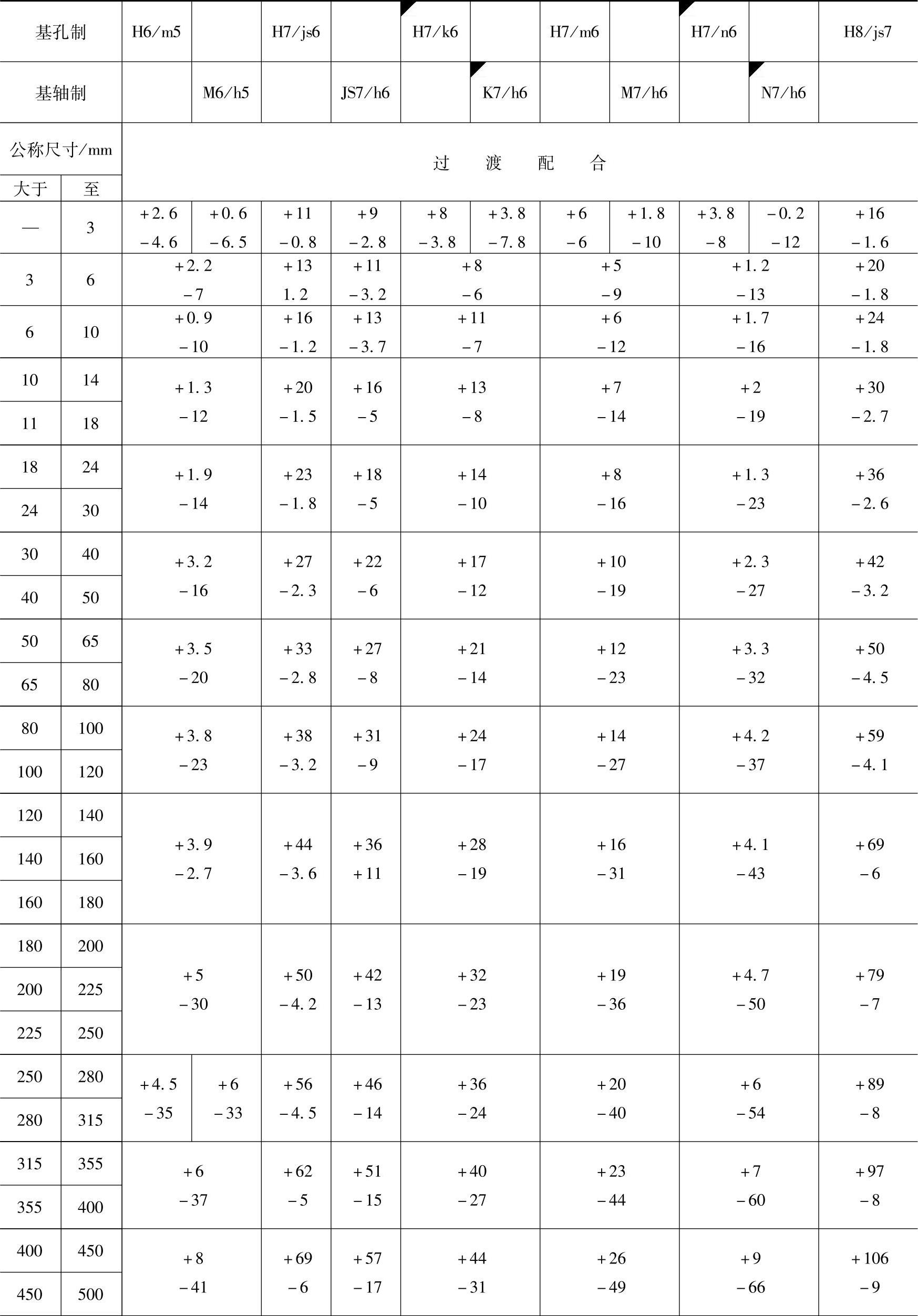
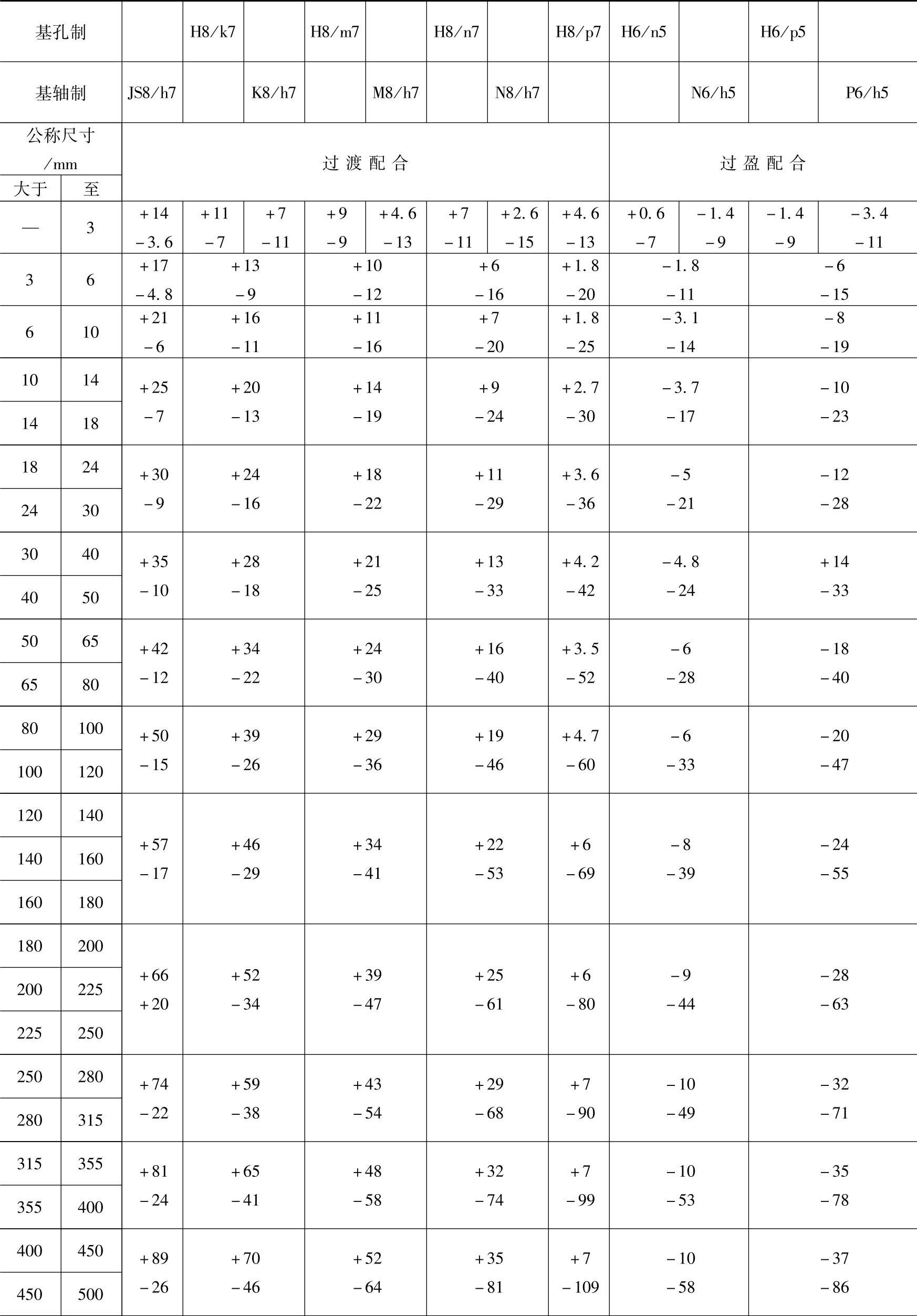
孔、轴实际尺寸按正态分布（T∶W_c=2∶1，P_cmin=86%）时，优先与常用配合的统计极限“间隙或过盈”见表1-52。

3）应用示例

例1 根据使用要求，某机床部件的配合为φ40H8/h7，但应避免偏差为零的孔、轴装配在一起，为此采用统计公差。

假设孔、轴尺寸趋近正态分布，规定

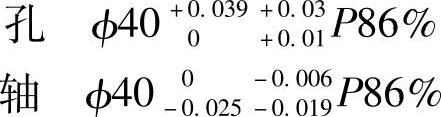
此时 孔公差T_H=0.039mm

轴公差T_S=0.025mm

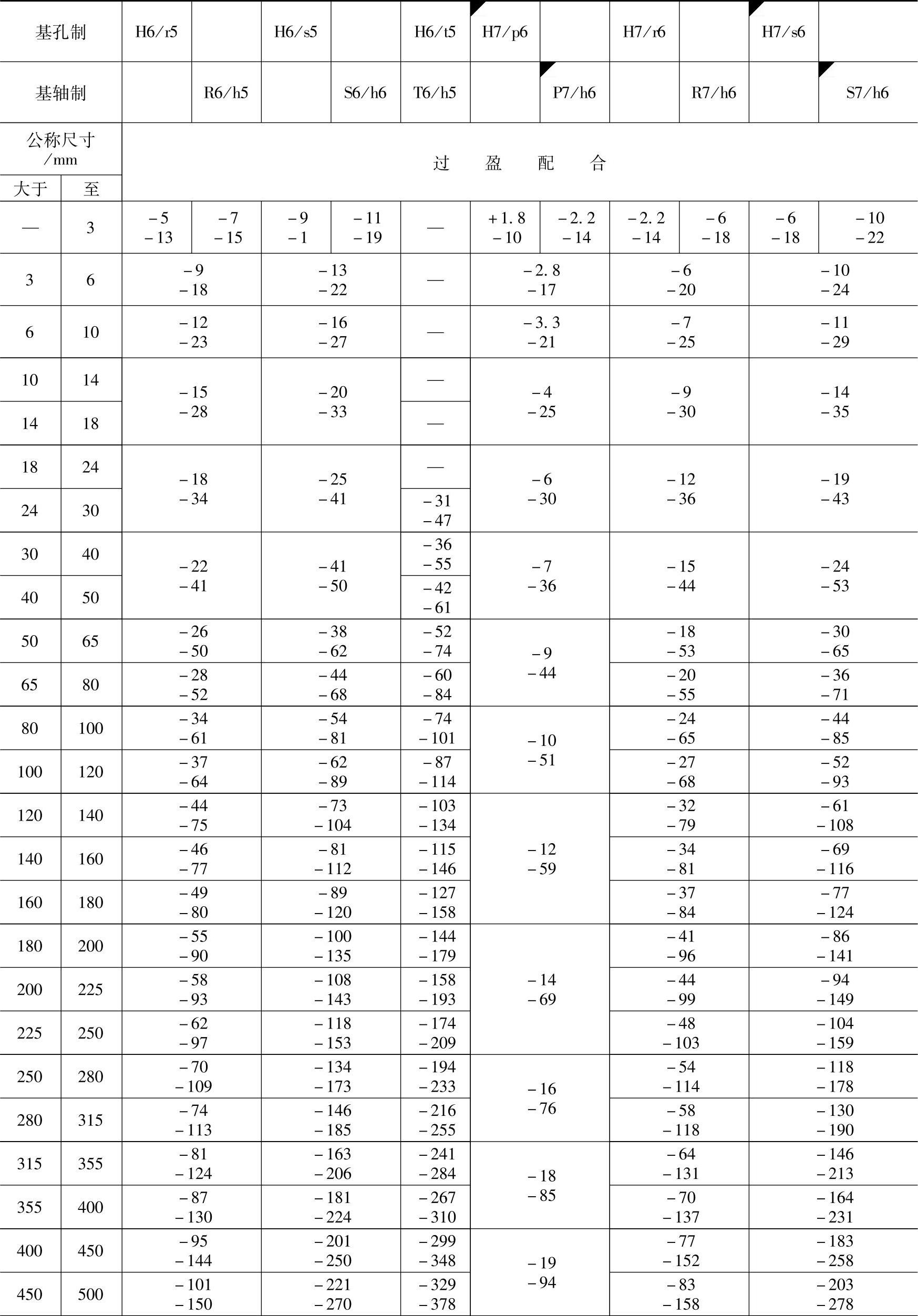
表1-52 优先与常用配合的统计极限“间隙或过盈”（T∶W_c=2∶1，P_cmin=86%）

（续）

（续）

（续）

（续）

（续）

（续）

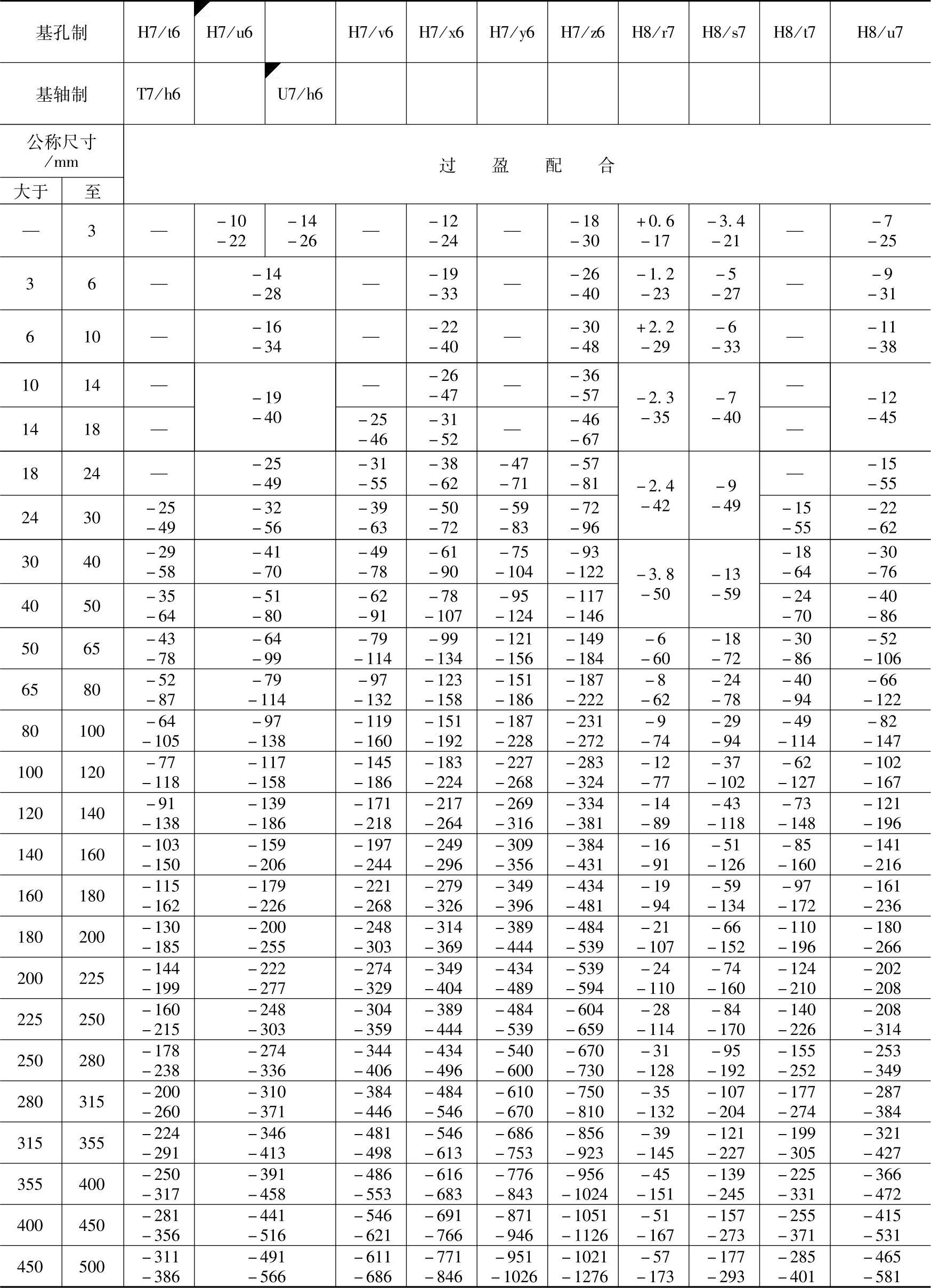
注：1.表中“+”值为间隙量，“-”值为过盈量。

2.标注◤的配合为优先配合。

配合公差T_F=0.039+0.025=0.064mm

孔公差比轴公差低一级，由简化计算公式得

T_PF=0.73T_F=0.73×0.064≈0.046mm

统计最小间隙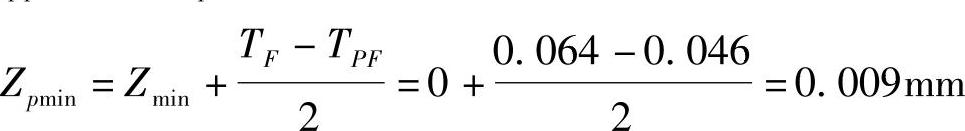

统计最大间隙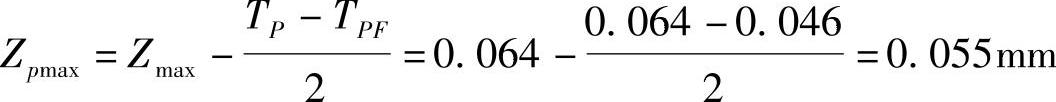

由上可见，孔、轴在装配时基本不会发生间隙为零的不利情况。

上述结果亦可利用表1-52直接查出如下：

Z_pmin=0.009mm

Z_pmax=0.055mm

此法更为简便快捷。

图1-35为本例的统计尺寸公差图解。

图1-35 例1统计尺寸公差图解

例2 某部件的配合选为φ60H8/g7间隙为+0.01～+0.086mm，但设计要求，间隙在+0.020～+0.078mm之间使用性能最好，为此采用统计尺寸公差：

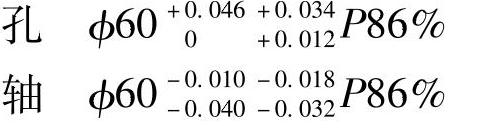
此时，将有86%的孔、轴装配后的间隙在0.02～0.076mm之间，即处于最好间隙状态。

例3 某传感器摇臂孔与轴的公称尺寸为2.5mm，根据性能要求装配后的间隙应在2.5～7.5μm内，若选

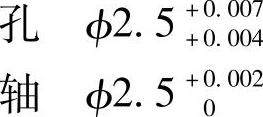
则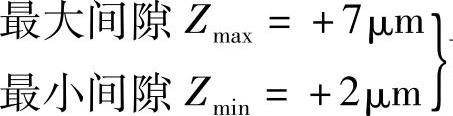可以满足设计要求，此时孔公差等级为IT4，轴公差等级为IT3，加工精度等级过高，工艺上难以实现，且为小批生产，不便进行分组装配。为此，采用统计公差，即

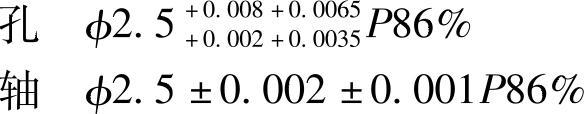
取置信度，1-α=95%，查得K_α=1.96。由简化计算公式得

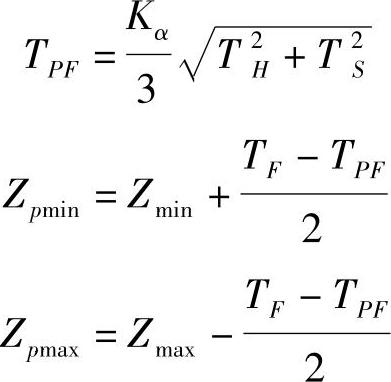
可计算出Z_pmin=2.64μm

Z_pmax=7.36μm即95%以上零件可满足设计要求，而此时孔公差为IT6，轴公差为IT5，工艺上较容易实现。

由以上三例可以看出，应用统计尺寸公差可对孔、轴配合取得不同的经济技术效果，避免孔、轴在装配时极限尺寸相逢的概率；获得最佳间隙或过盈的配合；适当降低孔、轴公差等级，解决工艺上的难度，降低加工成本。足见统计尺寸公差在生产实践中的意义。