递阶层次结构与权重分值优化

采用层次分析法分析影响水经济价值的低效因素，具体步骤如下。

（1）将农产品成本收益调查多元素作为一个系统，建立递阶层次结构。按照要素之间的类别和层级，对各要素进行有机组合和层次划分，划分为目标层、准则层和四级指标层。最高层是目标层，期望系统净效益最大，即农民增收、水经济价值最大；第二层准则层，是实现目标所必须采取的行为规范和限制措施，将投入小、产出大、用水量少作为准则进行规范；其下设四级指标层，对目标进行特征描述。通过对有关要素的相互结合、协同、逐层分析归纳，实现农产品水经济价值的最大化，层次结构划分如表7.20所示。

（2）建立判断矩阵。从指标层开始，针对上层准则或某个元素，对下层与之相关的元素进行两两对比，并按重要程度采用1～9比例标度法进行标度，标度值含义列于表7.21。对于相同类别的要素，通过比较按照标度权重进行矩阵排列，构建判断矩阵评定等级。

表7.20　指标层次结构及权重分值

注　括号中的数字为权重分值按由大到小顺序排位。

表7.21　1～9标度含义

分析中采用的四级指标判断矩阵群如下：

第一级：包括投入和产出两类指标，对于净效益最大化、农民增收来讲，两个指标同等重要，判断矩阵为：

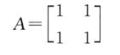
第二级：包括投入和产出两个指标矩阵，投入矩阵B1包括生产费用（元/亩）、技术与管理（元/亩）两个指标。其中生产费用（种子、化肥等）是农业生产的物质基础，我们期望系统投入小、生产成本低，同时也期望技术与管理投入高，以提高技术水平促进生产成本下降，因此，两类指标的重要程度排序为生产费用类稍重要于技术与管理费用类。产出矩阵B2包括农产品销售价格（元/kg）、产量（kg/亩）、补贴（元/亩）三个指标，鉴于粮食价格不可能放开任由市场调控，而补贴又只针对特殊农产品，故采用的重要程度排序为产量＞销售价格＞补贴。相应判断矩阵分别为：(www.xing528.com)

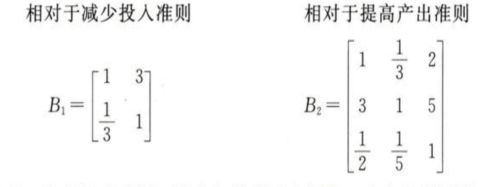
第三级：包括生产费用、技术与管理两个矩阵。生产费用矩阵C1包括原材料（元/亩）、劳动力（元/亩）、辅助性生产（元/亩）三个指标，采用的重要程度排序为原材料＞辅助性生产资料＞劳动力。技术与管理矩阵C2包括税金、管理、财务、销售、技术费5个要素，重要程度排序为技术服务＞销售＞管理＞财务＞税金。判断矩阵分别为：

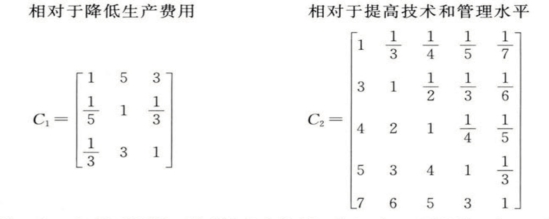
第四级：包括原材料、辅助性生产资料两个矩阵。原材料矩阵D1包括种子（元/亩）、化肥（元/亩）、农家肥（元/亩）、农药（元/亩）、农膜（元/亩）和土地（元/亩）6个要素，重要程度排序依次为土地、种子、化肥、农药、农家肥、农膜。辅助性生产资料矩阵D2包括畜力、机械作业、排灌、燃料动力、工具材料、修理维护和固定资产折旧7个要素，重要程度排序依次为排灌、机械作业、燃料动力、固定资产折旧、工具材料、修理维护、畜力。判断矩阵分别为：

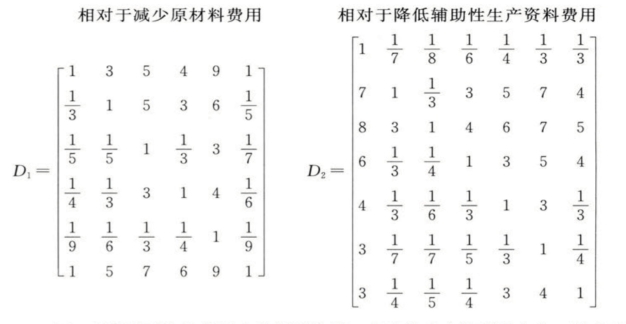
（3）对上述矩阵进行最大特征根计算，确定其相应的特征向量，从上到下依次推导得出各层级要素对于系统目标的组合权重，计算结果参见表7.20。通过上述递阶层次矩阵分析，将四级指标关系和各层指标的隶属关系通过权重分值明确表达出来。指标等级越高、权重越大，影响作用越显著，并制约下一级指标的权重值范围，需要慎重对待高级指标。为了辨析一级指标的影响，根据部分专家的意见产出受投入的影响，设投入指标稍重要于产出，A判断矩阵变为A'：

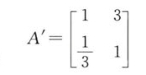
则指标权重变为投入0.75、产出0.25，A与A'对下层矩阵、指标排位和权重影响列于表7.22。从表可见，由于A矩阵标度变化，前11位指标排序和权重发生了变化，但自12位以后指标排序未变，且权重值改变不大，即前11个指标合计权重A矩阵为90%，A'矩阵为85%，因此，可以认为一级指标按照投入与产出同等重要、投入比产出稍重要两种方式标度，系统的显著性指标变化不大，可将前11个指标作为系统状态判定的显著性影响因素，并按照投入与产出同等重要模式进行低效影响因素分析。

表7.22　A和A'矩阵的指标排序与权重

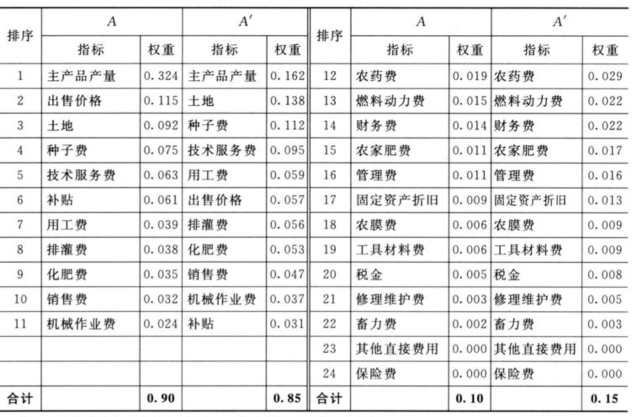
注　A表示投入与产出同等重要；A'表示投入比产出稍重要。

从表7.22可见，权重分值排在前11位的要素从大到小依次是主产品产量、出售价格、土地、种子、技术服务、补贴、用工、排灌费、化肥、销售费、机械作业，由于投入、产出属于同一级别，主产品产量、出售价格属于产出下的二级指标，而土地、种子属于投入下的四级指标，故前两者的权重分值高于后两者。