机械加工中的自激振动优化方案

图4⁃9 电铃的工作原理

1—电池 2—电磁铁 3—铃 4—弹簧片 5—触点 6—衔铁 7—按钮

自激振动是切削加工中经常出现的另一种形式的强烈振动。这种振动是由振动过程本身引起切削力的周期性变化，这个周期变化的切削力反过来又加强和维持振动，使振动系统补充了由阻尼作用消耗的能量。这种类型的振动称为自激振动。切削过程中产生的自激振动是频率较高的强烈振动，通常又称为颤振。颤振常常是影响加工表面质量及生产效率的主要因素。

1.自激振动的概念

下面用常见的电铃的工作原理来说明切削中的自激振动现象。电铃（见图4⁃9）是以电池1为动力源。当按下按钮7时，电动通过5—4—2与电池构成通路，电磁铁2产生磁力吸引衔铁6带动小锤敲击铃了。当弹簧片4被吸引时，触点5处断电，电磁铁失去磁性，小锤靠弹簧片4弹回原处，接着又重复刚才所述的过程而形成振动。这种振动过程不存在外界周期干扰，所以不是强迫振动。它本身是由悬臂弹簧片4和小锤组成振动元件，以及由衔铁6、电磁铁2、电路组成调节元件，产生交变力。交变力使振动元件产生振动，这就是激振。振动元件又对调节元件产生反馈作用，以便产生持续的交变力，如图4⁃10所示。小锤打击电铃的频率由弹簧片、小锤及衔铁本身的参数（刚度、质量及阻尼）所决定。而阻尼和运动摩擦所损耗的能量由系统本身的电池供应。这个过程就是区别于强迫振动的自激振动。

金属切削过程的自激振动，也由上述两个基本部分组成（见图4⁃10）。切削过程产生交变力ΔF，激励工艺系统，工艺系统产生振动位移Δy，再反馈给切削过程。维持振动的能量来源于机床的能源。

自激振动的特点：

1）自激振动是一种不衰减振动。振动过程本身能引起某种力周期性地变化。振动系统能通过这种力的变化，从不具备交变特性的能源中周期性地获得能量补充，振动从而得到维持。而外界的干扰有可能在最初触发振动时起作用，但它不是产生自激振动的直接原因。

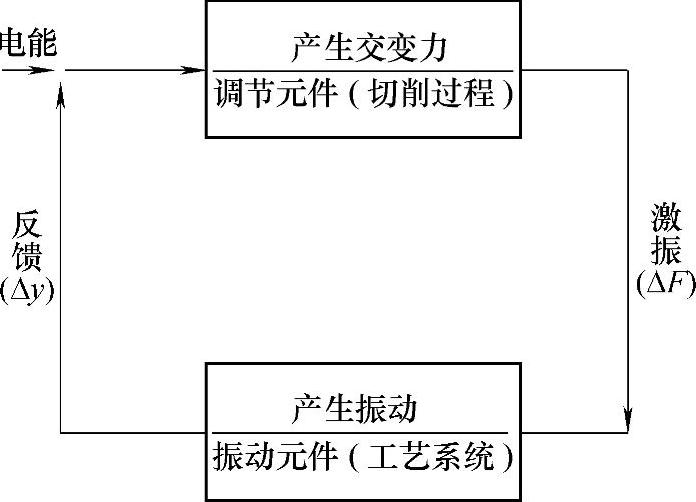
图4⁃10 电铃的自振系统

2）自激振动的频率接近或等于系统的固有频率，即由系统本身的参数所决定，这是与强迫振动最大的区别。

3）自激振动是否产生以及振幅的大小，决定于每一振动周期内系统所获得的能量与所消耗的能量的对比情况。如果获得的能量大于消耗的能量，如图4⁃11中的A₁，则振动将继续加强，振幅将不断增大；反之，则振动减弱，振幅将不断减小，如图4⁃11中的A₂。振幅一直增加或减小到其所获得的能量和消耗的能量相等时为止。而振幅的减小意味着自激振动的消失，当振幅在任何数值时获得的能量都小于消耗的能量，则自激振动根本就不可能产生。如图4⁃11所示，E⁺为获得的能量，E-为消耗的能量，可见只有当E+和E-的值相等时，振幅达到A_o值，系统处于稳定状态。

图4⁃11 自激振动的能量关系

4）自激振动的形成和持续 是由于过程本身产生的激振和反馈作用，所以若停止切削过程，即使机床仍继续空转，自激振动也随即消失。因此，可以通过切削试验来研究工艺系统的自激振动。同时，也可通过改变切削过程有影响的工艺参数来控制切削过程，从而限制自激振动的产生。

2.产生自激振动的学说

关于切削过程产生自激振动的原因，虽经长期研究，但目前尚无一种能阐明各种情况下产生自激振动的理论。下面介绍三种解释自激振动的学说：

（1）负阻尼（负摩擦）激振原理 这是早期解释切削自激振动产生原因的一种理论。当切削韧性钢材时，径向切削分力F_y开始时随着切削速度的增加而增加，但当达到某一速度极限后，则又随着切削速度的增加而减小，如图4⁃12所示。试验证明，在切削分力—切削速度曲线下降区板易引起切削自振。由切削理论可知，径向切削分力F_y的大小，主要决定于切屑沿刀具前面相对滑动所产生的摩擦力。因此，切削分力的改变就意味着摩擦力的变化。把摩擦力随摩擦速度的增加而下降的特性称为负摩擦（负阻尼）特性。

图4⁃12a为车削加工示意图，可以将其简化为单自由度振动系统。刀具相当于重物，只能作y方向运动，刀架相当于弹簧。图4⁃12b为径向切削分力F_y与切屑和刀具前面相对摩擦速度v的关系曲线图。当稳定切削时，工件表面的切削速度为v_o，而刀具和切屑的相对滑动速度为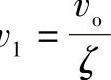（ζ—为切屑收缩系数）。当刀具产生振动时，刀具前面与切屑的相对摩擦速度将受振动速度y的影响而发生变化。在刀具切入工件时，相对摩擦速度为v₁+y；刀具切出工件时其相对速度为v₁-y；它们各自对应的径向切削分力F_y1和F_y2。由图4⁃12b看出刀具切入的半个周期中，切削分力小于刀具切出的半个周期的切削分力。因而其所作的负功（因刀具的运动方向与切屑流出方向相反做负功）也小于刀具切出时所做的正功（刀具运动方向与切屑流出方向相同做正功）。在一个振动周期中，便有多余的能量输入振动系统，振动将继续维持下去。

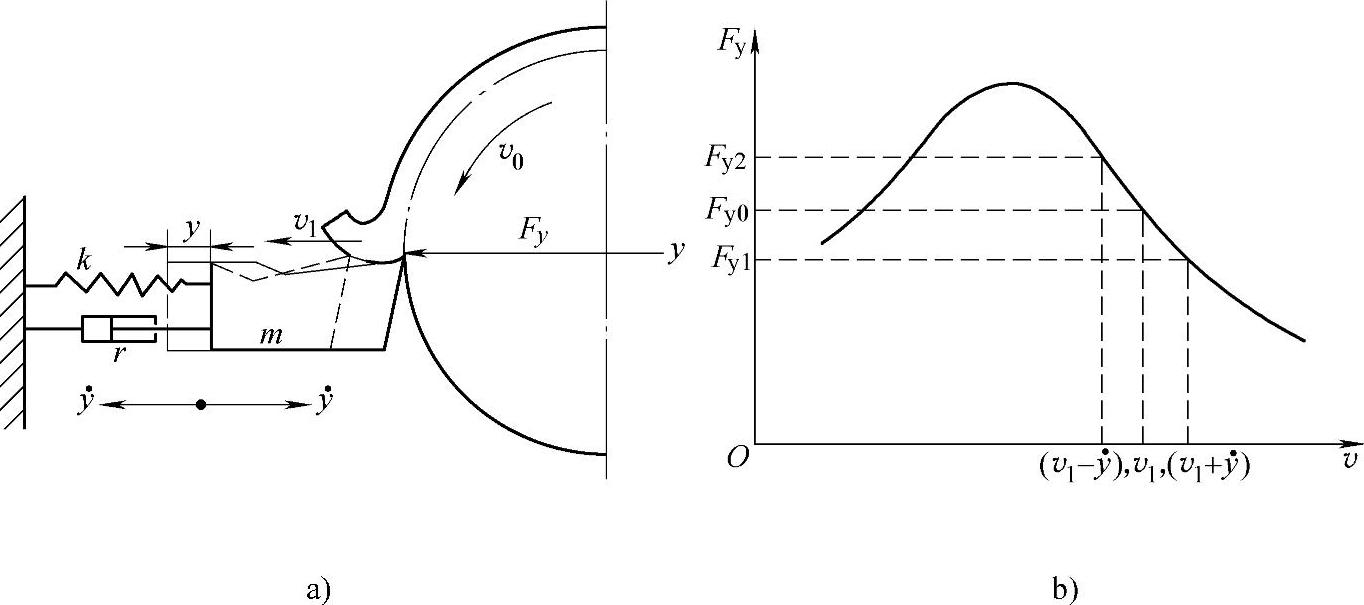
图4⁃12 负阻尼激振原理

a）车削加工示意图 b）径向切削分力F_y与切屑和刀具前面相对摩擦速度v的关系曲线图

（2）再生自激振动原理 在切削（或磨削）加工中，由于刀具（砂轮）的进给量一般不大，而刀具的副偏角又较小，当工件转过一圈开始切削下圈时，刀刃必然与已切过的上一圈表面接触，即产生重叠切削。图4⁃13为磨削加工示意图，设砂轮宽度为B，工件每转进给量为f，工件后一转的磨削区和前一转的有重叠部分，其大小用重叠系数_μ表示

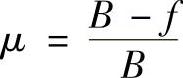
一般情况下0<μ<1。

在稳定的切削过程中，由于偶然的扰动（材料的硬疵点，加工余量不均匀或其他原因的冲击等），工艺系统会产生一次自由振动，并在被加工表面上留下相应的振纹。当工件转至下一转时，由于切削到重叠部分的振纹使切屑厚度发生变化，从而引起切削力的周期改变，产生再生自激振动（见图4⁃14）。这种周期改变的切削力，在加工中很容易引起自激振动，尤其当用宽刃车刀小进给纵车或切槽时，产生振动的现象最为常见。

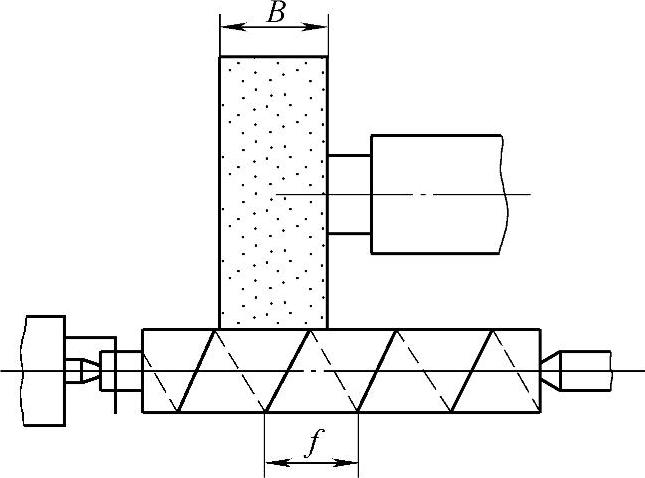
图4⁃13 磨削时重叠切削示意图

当然，如果加工系统的稳定性好，或者创造适当的条件，也不一定就产生自激振动。切削时还可将前一转留下的振纹表面切去，消除引起自激的根源。因此，就需要进一步分析系统在怎样的情况下被激发起自激振动。

为了说明上述问题，将切削过程用图4⁃14及图4⁃15所示的三种情况表示。图中y_o表示前一转切削的工件表面（实线），y表示后一转切削的工件表面（虚线）。从图4⁃15b看出，工件前后两圈之间没有相位差，即φ=0。因此其切削深度基本保持不变，切削力也保持稳定，再生自激振动亦不会产生。图4⁃14则表示y比y_o滞后一个相位角φ。因此，刀具在切入工件的半个周期中的平均切削厚度比切出时的平均切削厚度小。其切削力也比切出时为小。在一个振动周期中，切削力作的正功大于负功，这样便有多余的能量输入系统中去，使振动得到维持和加强。图4⁃15a则正好相反，其y比y_o超前一个φ角，刀具切入时平均切削厚度大于切出时的平均切削厚度。在一个振动周期中，切削力所作的负功大于正功，即系统消耗于阻尼的能量大于它所获得的能量。因此，振动即消失。由以上分析可知，切削中再生自激振动产生的必要条件是y滞后于y_o为了减小或消除再生自激振动，可以改变加工中某项工艺参数，使y与y_o同相或超前一个相位角。

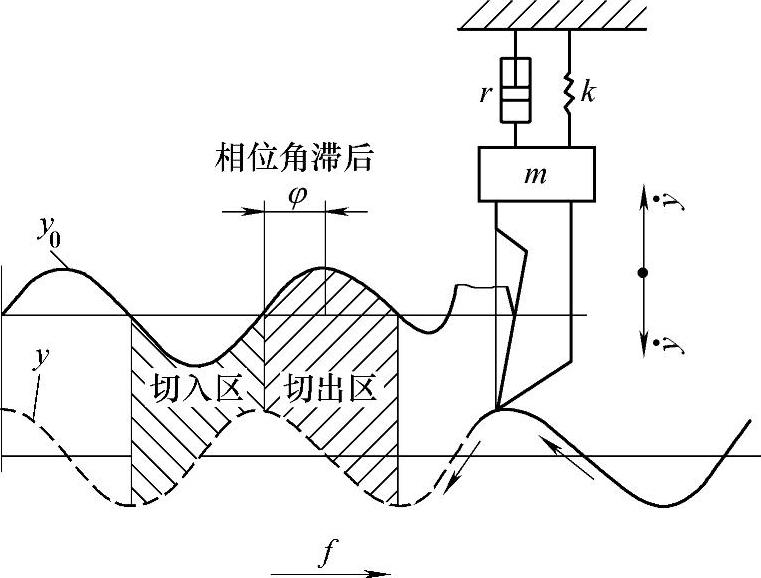
图4⁃14 再生自激振动示意图

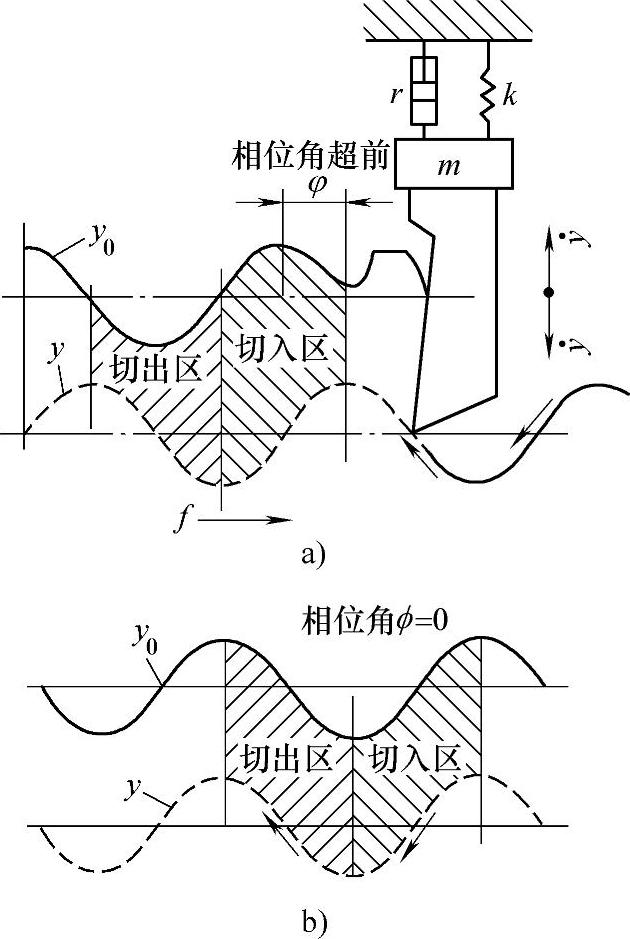
图4⁃15 再生自激振动分析图

a）工件前后两转之间其y比y_o超前一个φ角 b）工件前后两转之间没有相位差

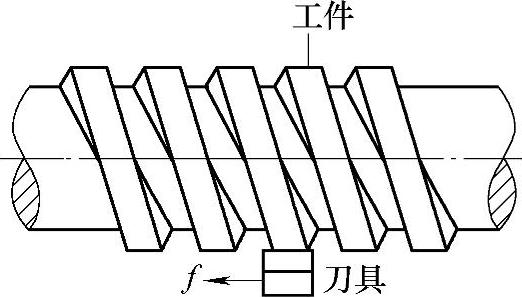
图4⁃16 纵车方型螺纹外表面

（3）振型耦合自激振动原理 当纵车方型螺纹的外圆表面时，如图4⁃16所示，刀具并不发生重叠切削，从理论上讲排除了再生自激振动的可能性。但实际加工中，当切削深度达到一定值时，仍然会产生自激振动。其原因可用“振型耦合理论”说明。

振型耦合原理，又称坐标联系原理。这个原理是在排除再生自振的条件下，对切削过程的自激振动现象进行解释的学说。它主要用于说明多自由度系统的自振现象。图4⁃17所示为这种系统最简单的例子。它包括质量m悬挂于两个相互垂直且刚度不同的弹簧k₁、k₂上。

在图4⁃17所示的条件下，为了排除再生自振的影响，必须在特定的加工条件下，使刀具总是切到“新鲜”金属。如果系统在切削中一旦产生了角频率为ω的振动，则质量m同时在两个方向x₁和x₂，以不同的振幅和相位进行振动。其合成运动为一椭圆E。假定刀具的运动按图中箭头所示方向，当由A到B的前半周期中系统消耗能量，而在后半周期中切削力将能量输入系统。由于在后半周期平均切削深度较大，故后半周期中平均切削力大于前半周。因此，在一个振动周期内，输入系统的能量大于系统消耗的能量，多余的能量是以抵偿阻尼损耗，振动将得以维持。

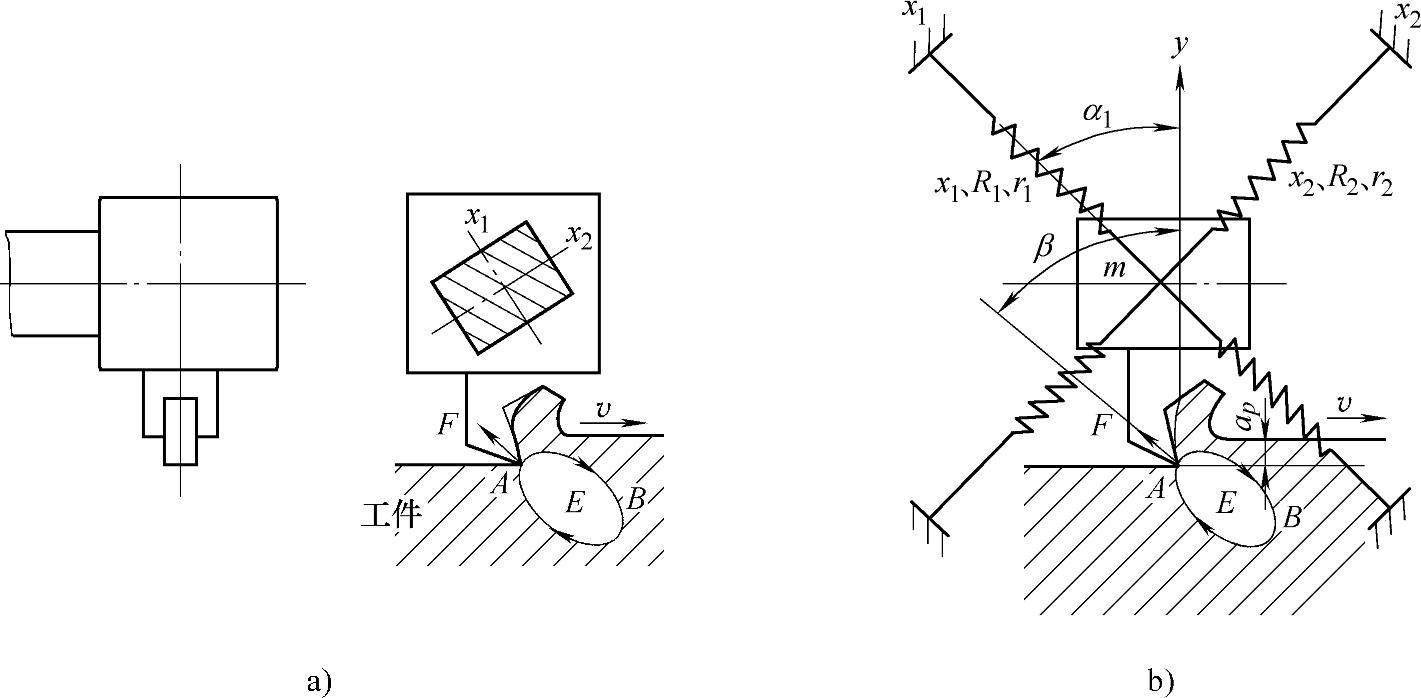
图4⁃17 两个自由度的耦合振动系统

a）切削模型 b）动力学模型

3.控制自激振动的途径

从上述分析讨论可知，切削自激振动既与切削过程本身有关，又与工艺系统的结构性能有关，所以消除振动的措施也是多方面的。但最中心的问题是减小内激振力。下面从工艺角度出发介绍一些基本措施。

（1）合理选择切削用量 切削速度v的选择，可参阅图4⁃18所示车削时速度与振幅的关系曲线。一般当v=30～70m/min范围内容易产生振动，相当的振幅值较大。但切削速度高于或低于这个范围，振动处于减弱状态，在许多情况下采用高速切削是很合理的，它即可避免自激振动，又能提高生产率和低的表面粗糙度Ra值。(www.xing528.com)

从图4⁃19看出，增大进给量f可使振幅A减小，所以在加工表面粗糙度允许的情况下，可选取较大的进给量以避免自激振动。

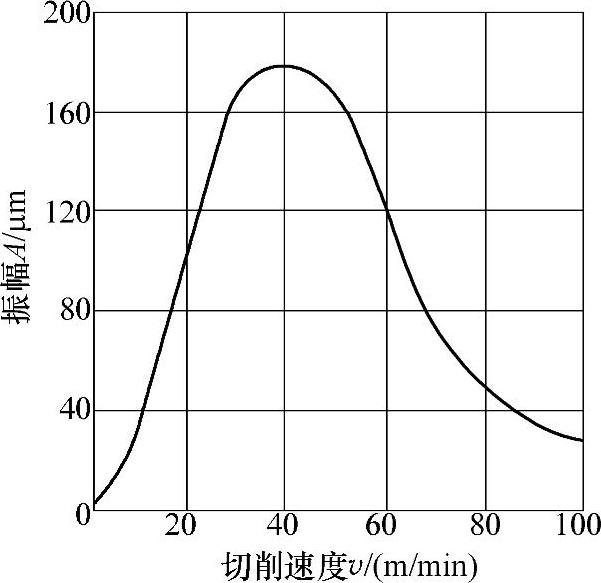
图4⁃18 切削速度v与振幅的关系

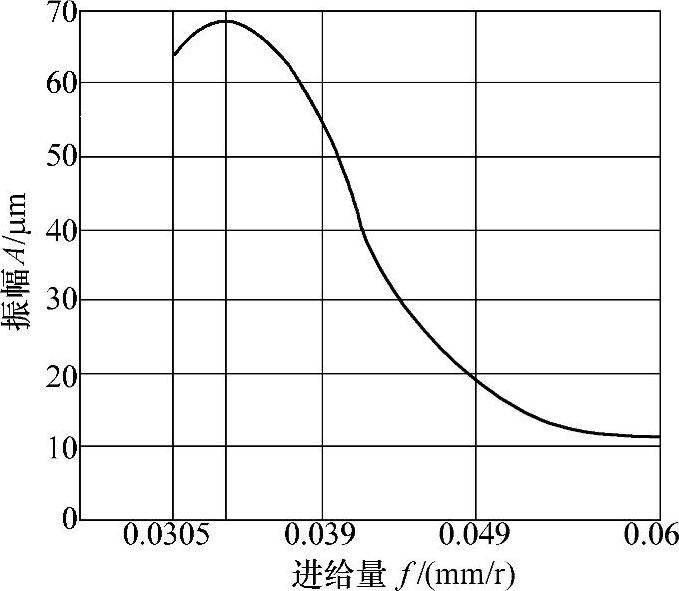
图4⁃19 进给量与振幅的关系

根据背吃刀量a_p与切削宽度b的关系，当a_p增加时，b也增加。图4⁃20表明，随着a_p的增大，振动不断加强。这是由于切削宽度b对振动影响较大，所以选择a_p时一定要考虑切削宽度b对振动的影响。

（2）合理的选择刀具几何参数 刀具的主偏角k_r和副偏角k_r应尽可能选得适当，它们对径向切削分力影响较大。在工艺系统刚度较低（车阀杆、镗孔）的条件下，更应取得大些。图4⁃21表示主偏角对振动强度的影响很大。

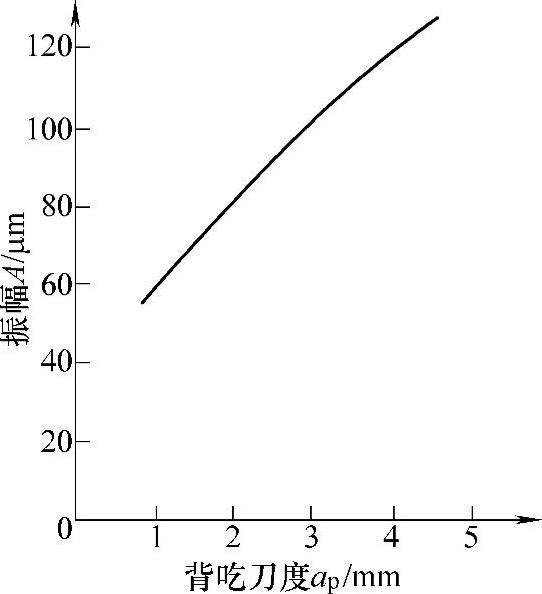
图4⁃20 背吃刀量与振幅的关系

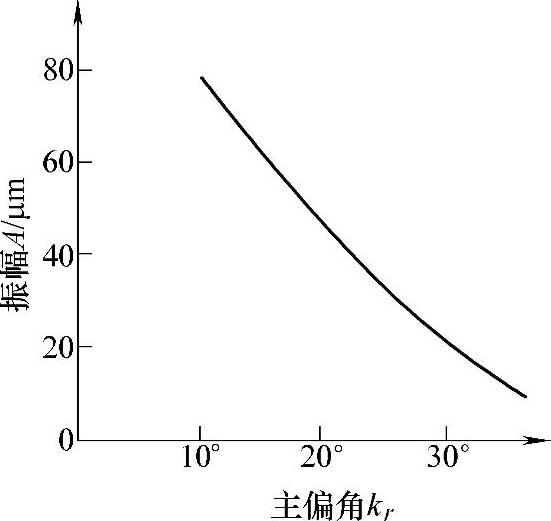
图4⁃21 主偏角k_r对振幅的影响

图4⁃22 前角γ_o对振幅的影响

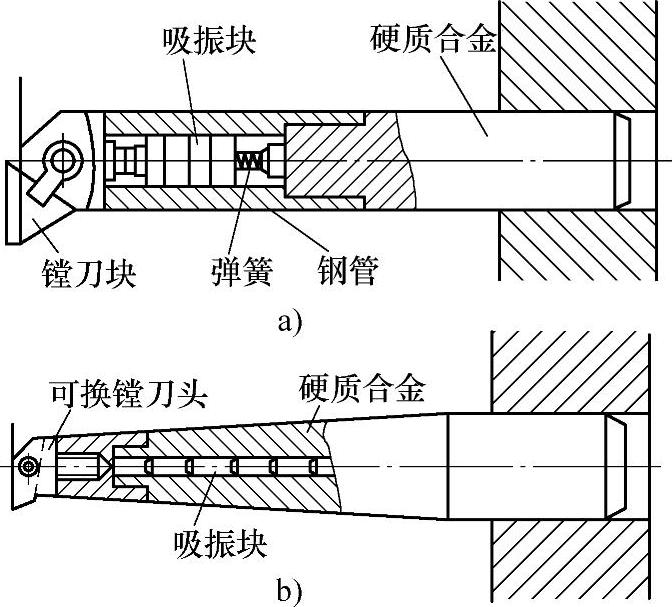
图4⁃23 复合结构镗刀杆

a）圆柱形结构镗刀杆 b）圆锥形结构镗刀杆

前角γ_o对振动强度的影响也很大，如图4⁃22所示。前角愈大切削过程愈平稳，所以应采取正前角（γ_o>0°）。有时为了提高刀具的耐用度，还可磨出倒棱。

后角α_o应尽量取小些，但不能太小，以免刀具后面与加工表面之间发生摩擦，反而容易引起振动。通常在刀具的主后刀面上磨出一段负的倒棱，能起到很好的消振作用，此种刀具也称消振车刀。

（3）提高工艺系统的抗振性

1）提高机床的抗振性。对于使用中的机床，主要是确切地了解机床的动态特性，掌握其薄弱环节，然后在使用时采取适当的措施提高其抗振性。如薄弱环节的动刚度，往往受连接面的接触刚度的影响，故用增强连接刚度等方法，提高机床结构系统的抗振性。

2）提高刀具和工件的抗振性。对于刀具，一般要求它具有较高的弯曲与扭转刚度、高的阻尼系数和固有频率。图4⁃23所示为具有高固有频率的复合结构镗刀杆，这种刀杆夹持端使用高弹性系数的硬质合金，而刀头端使用重量约为硬质合金1/2的钢管。使用钢管不仅能减少有效质量，而且有利于加工和组装。图4⁃23b中的材料与图4⁃23a中的相同，但其圆锥形的结构则具有较高的动、静刚度。

加工中，工件的抗振性，主要取决于工件的安装方法。对于细长阀杆，为了提高其弯曲刚度，常使用中心架和退刀架。

（4）采用减振装置 当使用上述各种措施仍然不能达到消振的目的时，可考虑使用减振装置。减振装置具有结构轻巧、效果显著等优点。对于消除强迫振动和自激振动同样有效，已受到广泛的重视和应用。

减振装置可分阻尼器和吸振器两种：

1）阻尼器的基本原理及应用。阻尼器是基于阻尼的作用，把振动能量变成热能消散掉，以达到减少振动的目的。阻尼越大，减振效果越好。常用的有固体摩擦阻尼、液体摩擦阻尼和电磁阻尼等。

图4⁃24表示利用多层弹簧片相互摩擦，消除振动能量。图4⁃25表示利用液体流动阻力的阻尼作用消除振动。

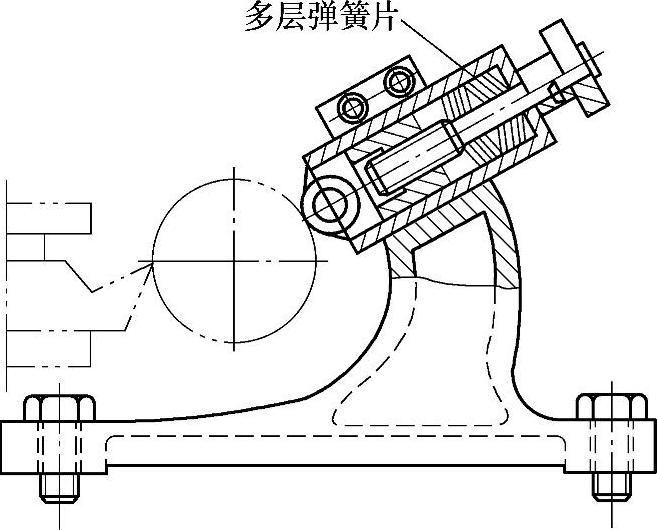
图4⁃24 干摩擦阻尼器

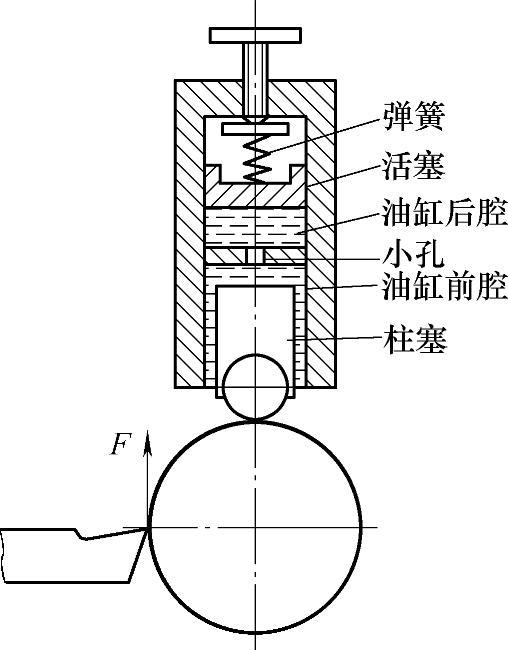
图4⁃25 液压阻尼器

2）吸振器的原理及应用。吸振器又分动力式吸振器和冲击式吸振器两种：

①动力式吸振器。是用弹性元件把一个附加质量连接到振动系统上的吸振装置。其减振原理与摩擦阻尼器不同。它不是依靠消耗能量来减振，而是利用附加质量的动力作用，使弹性元件加在系统上的力与系统的激振力尽量相抵消，以此减小振动。

图4⁃26表示用于镗刀杆的有阻尼动力吸振器。这种吸振器用微孔橡胶衬垫做弹性元件，并有附加阻尼作用，因而能得到较好的消振作用。

②冲击式吸振器。冲击式吸振器是由一个自由冲击的质量与壳体所组成。当系统振动时，由于自由质量的往复运动。产生冲击消耗了振动的能量，因而可减小振动。

图4⁃27所示为螺栓式冲击消振器。当刀具振动时，自由质量1也振动，但由于自由质量与刀具是弹性连接，振动相位相差180°。当刀具向下挠曲时，自由质量却克服弹簧的弹力向上移动。这时自由质量与刀杆之间形成间隙δ。当刀具向上运动时，自由质量以一定速度向下运动，产生冲击而消耗能量。此外，螺纹结合面，以及弹簧与相配零件接触表面上摩擦力，均消耗一部分能量。图4⁃23所示的复合结构镗杆，其前端的结构就是根据冲击式吸振的原理而设计的。

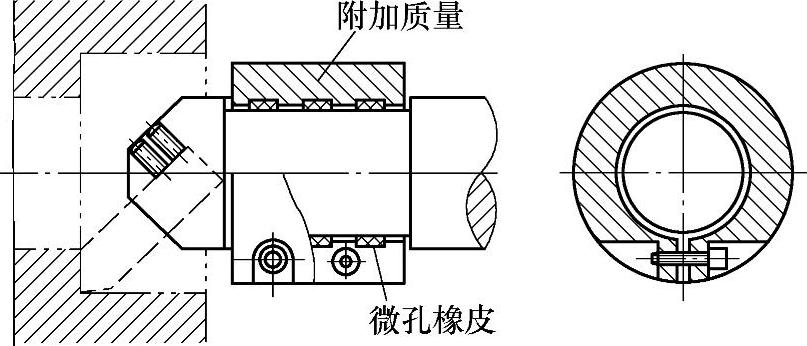
图4⁃26 用于镗刀杆的动力吸振器

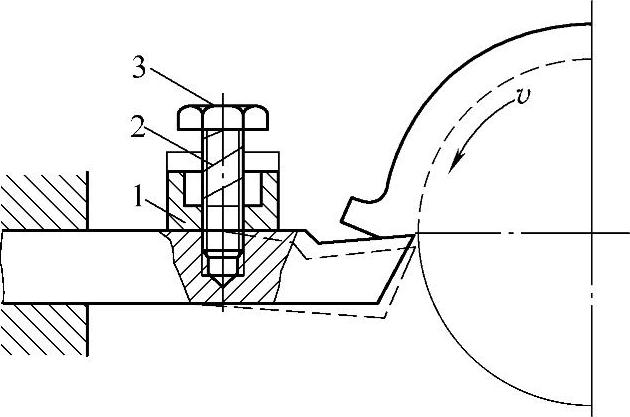
图4⁃27 冲击式消振器

（5）合理调整振型的刚度比 根据振型耦合原理，工艺系统的振动还受到各振型的刚度比及其组合的影响。合理地调整它们之间的关系，就可有效地提高系统的抗振性，抑制自激振动。

图4⁃28即为应用上述原理所做的实验。图a为实验时所用的削扁镗杆，刀头2用螺钉3固定在镗杆的任意角度位置上。镗杆1削扁部分的厚度a=（0.6～0.8）d，其中d为镗杆直径。镗杆削扁后两个相互垂直的振型具有不同的刚度k₁和k₂，再通过刀头2在镗杆上的转位调整，即可找到稳定性较高的方位角α（α为加工表面法向与镗杆削边垂线的夹角），从而消除自激振动，提高生产效率。

图4⁃28b所示为用偏刀镗孔时（镗杆a=0.8d，v=40m/min，f=0.3mm/r，a_p=3mm，镗杆的伸出长为550mm），削扁镗杆的双振幅与方位角α的关系。如图4⁃28所示，当115°<α<150°镗孔时，就不会出现自激振动。

图4⁃28c表示由实验求得的极限背吃刀量a_plim与方位角α的关系。图中“8”字形线所包围的范围表示稳定区。由图可看出，最适宜的方位角在α=120°～140°（或α=300°～320°）之间。因此，适当的调整α就可使a_plim从0.3～0.5mm增加至6mm而不产生自激振动。

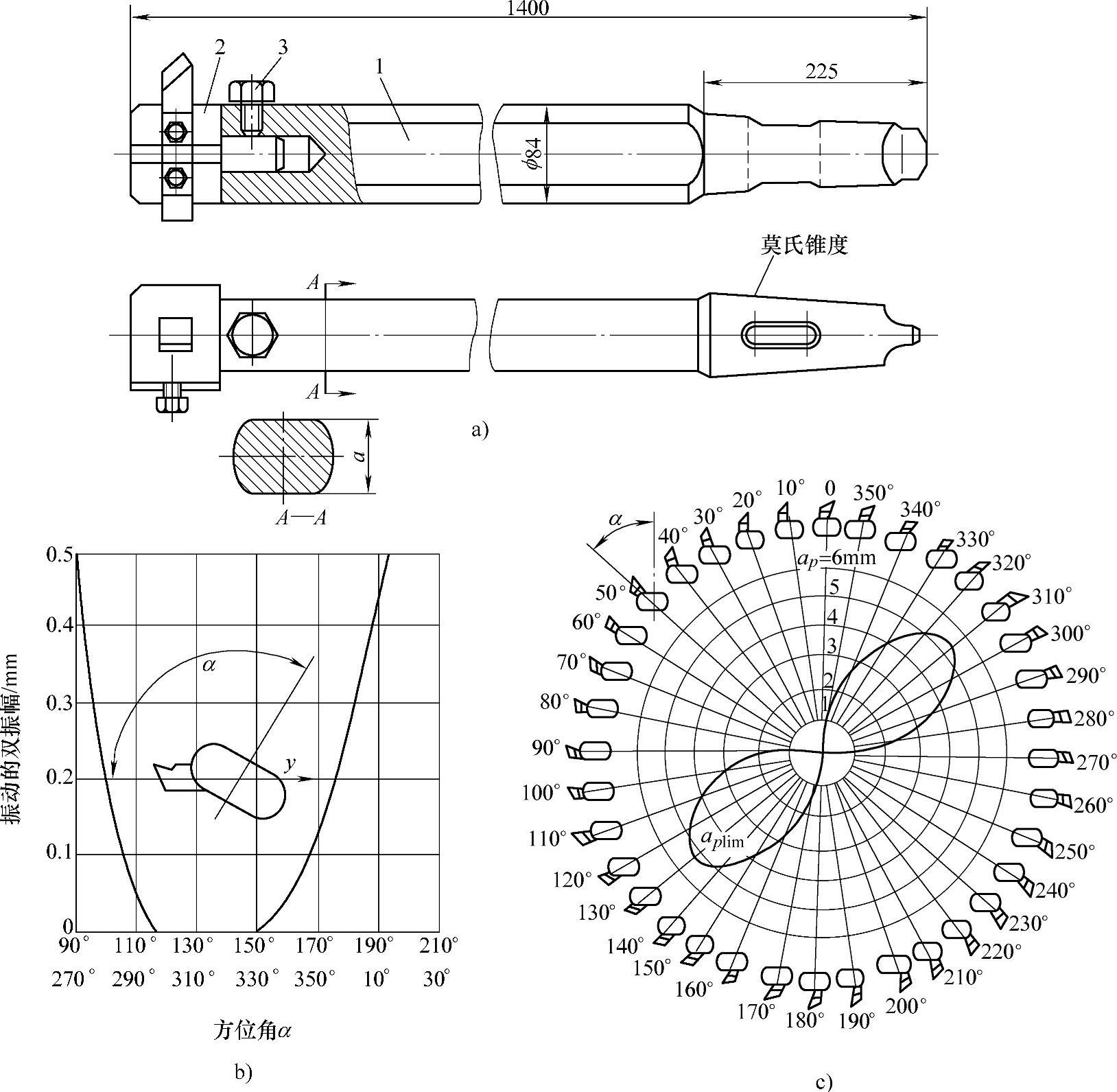
图4⁃28 削扁镗杆镗孔实验

a）实验时所用的削扁镗杆 b）用右偏刀镗孔时，削扁镗杆的双振幅与方位角α的关系 c）实验求得的极限切削深度a_plim与方位角α的关系