数制与码制的基础知识：二进制、十进制及补码

1.基本概念

所谓数码，就是数制中表示基本数值大小的不同数字符号。例如，二进制有两个数码：0、1；十进制有10个数码：0、1、2、3、4、5、6、7、8、9。

基数，就是指数制中所使用数码的个数。例如，二进制的基数为2；十进制的基数为10。

位权，是指数制中某一位上的1所表示数值的大小（所处位置的价值）。例如，十进制数123，1的位权是100，2的位权是10，3的位权是1。二进制数1011，从高位开始，第一个1的位权是8，0的位权是4，第二个1的位权是2，第三个1的位权是1。

2.常用的基本数制

在计数的规则中，人们使用最多的进位计数制中，表示数的符号在不同的位置上时所代表的数的值是不同的。

十进制是人们日常生活中最熟悉的进位计数制，十进制用D（decimal）来表示。在十进制中，数用0，1，2，3，4，5，6，7，8，9这十个符号来描述。计数规则是：逢十进一。

二进制是在计算机系统中采用的进位计数制，二进制用B（binary）来表示。在二进制中，用0和1两个符号来描述。计数规则是：逢二进一。

八进制用O（octal）来表示，八进制中包括0，1，2，3，4，5，6，7这八个符号。计数规则是：逢八进一。

十六进制是人们在计算机指令代码和数据的书写中经常使用的数制，十六进制用H（hexadecimal）来表示。在十六进制中，数用0，1，…，9和A，B，…，F等16个符号来描述。计数规则是：逢十六进一。

3.其他进制转换为十进制

方法：将其他进制按权位展开，然后各项相加，就可得到相应的十进制数。例如，将二进制的11010转换为十进制数的方法为

（11010）₂=1×2⁴+1×2³+0×2²+1×2¹+0×2⁰=16+8+2=（26）₁₀

4.将十进制转换其他进制

方法：把要转换的数除以新的进制的基数，把余数作为新进制的最低位；把上一次得的商再除以新的进制基数，把余数作为新进制的次低位；继续上一步，直到最后的商为零，这时的余数就是新进制的最高位。例如，将十进制的58转化为二进制，需要连续除以2取余数，即(www.xing528.com)

（58）₁₀=（111010）₂

5.二进制与八进制、十六进制的相互转换

二进制转换为八进制、十六进制的方法：它们之间满足23和24的关系，因此把要转换的二进制从低位到高位每3位或4位一组，高位不足时在有效位前面添“0”，然后把每组二进制数转换成八进制或十六进制即可。

八进制、十六进制转换为二进制时，把上面的过程逆过来即可。例如：

八进制：2 5 7·0 5 5 4二进制：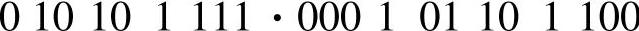

十六进制：A F·1 6 C

几种常用进制之间的对应关系如表5-1所示。

表5-1 几种常用进制之间的对应关系

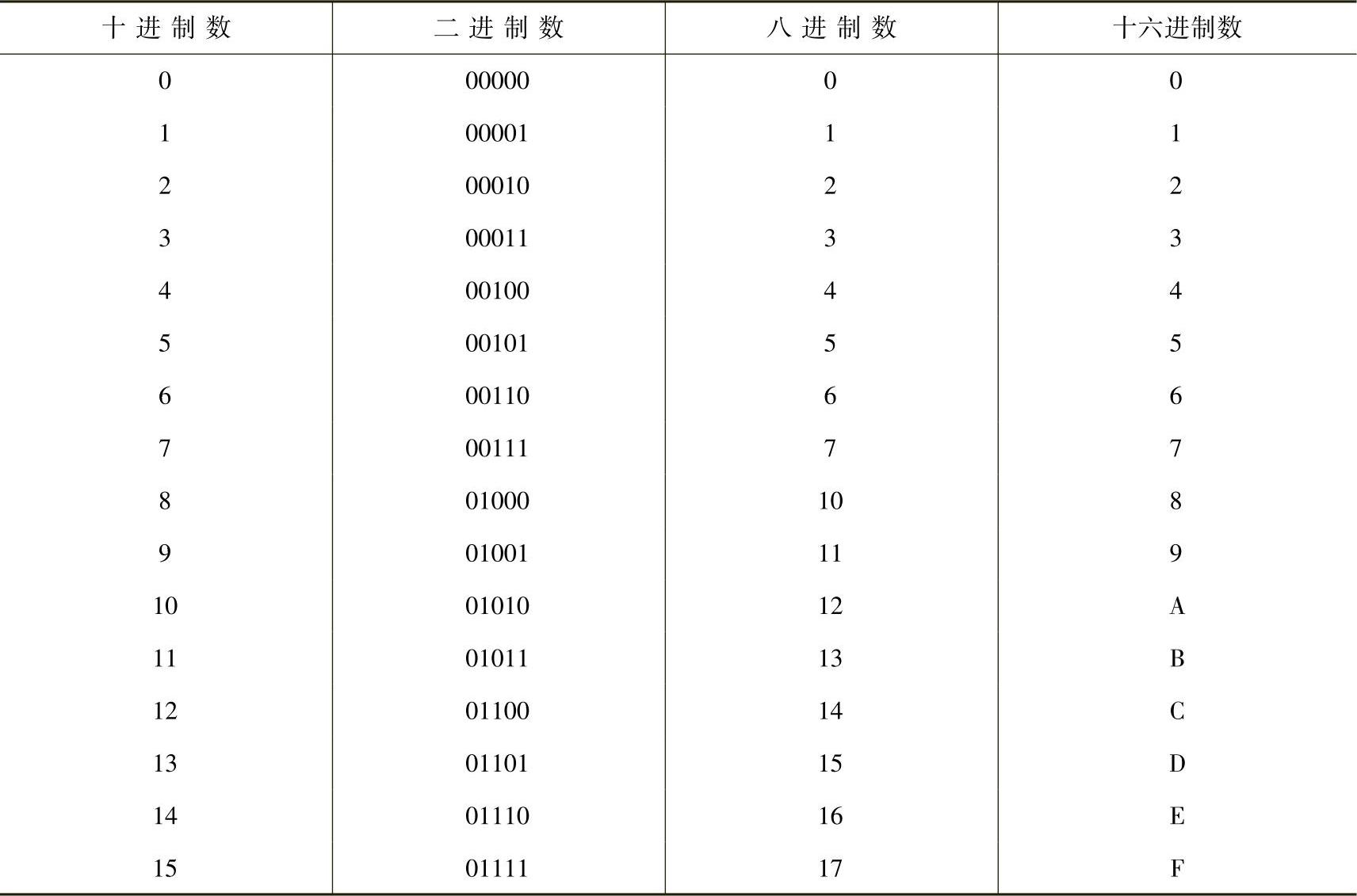
6.常用的码制

原码是用“符号+数值”表示，对于正数，符号位为0，对于负数，符号位为1，其余各位表示数值部分。

在反码中，对于正数，其反码表示与原码表示相同；对于负数，符号位为1，其余各位是将原码数值按位取反。

在补码中，对于正数，其补码表示与原码表示相同；对于负数，符号位为1，其余各位是在反码数值的末位加“1”。