模拟信号数字化及仿真实现方法

数字通信系统具有许多优点，而实际上，由信息转换成的原始电信号一般为模拟信号，这就需要利用数字通信系统传输模拟信号。

模拟信号数字化需要经过抽样、量化、编码才能完成。

PCM信号形成过程示意图如图2.1所示。

图2.1　PCM信号形成过程示意图

1.抽样

抽样定义：某一时间连续信号f（t），仅取f（t0）、f（t1）、f（t2）等各离散点数值。

2.量化

量化将连续的幅度值转变为离散的幅度值。

（1）均匀量化

均匀量化——将抽样值均匀地分为M个相等的间隔，M称为量化级数。

量化误差——抽样值与量化值差的绝对值，用e（kTs）表示。

其中，TS表示时间间隔；m（kTs）为抽样值；mq（kTs）为量化值。

量化信噪比——信号功率与量化噪声功率的相对大小。

其中，S表示输入量化器的信号功率；Nq表示量化噪声功率；E（x2）代表信号的平均功率。

均匀量化带来的问题：由于小信号太小，因此，不能满足通信质量要求。

对此，解决的方案就是非均匀量化。

（2）非均匀量化

常用的非均匀量化有μ律和A律两种压扩特性。

μ压缩律就是压缩器的压缩特性具有如下关系的压缩律：

其中，μ=255；x代表输入信号；y代表输出信号。

A压缩律就是压缩器的压缩特性。

其中，A=87.6。

要准确恢复信号，则扩张特性和压缩特性应该严格互逆，而μ律压缩、A律压缩都是用模拟器件实现的，难以做到严格互逆。目前应用较多的是用数字电路方式实现A律特性折线近似。A律压扩特性如图2.2所示。

图2.2　A律压扩特性图

实际应用中的两种折线：

13折线近似A=87.6的A律压缩特性；

15折线近似μ=255的μ律压缩特性。

A律13折线压扩特性如图2.3所示。

图2.3　A律13折线压扩特性图

3.编码

13折线分段时的X值和A律压扩特性（A=87.6）的X值的比较如表2.1所示。

表2.1　13折线分段时的X值和A律压扩特性（A=87.6）的X值的比较

在A律13折线编码中，采用8位折叠码，8位码的安排如下：

C1表示极性码，信号为正则C1=1，信号为负则C1=0；C2C3C4表示段落码，代表8个段落；C5C6C7C8表示段内码，代表每个段内的量化分级，4位段内码把每个段分为16个量化分级。

如果以非均匀量化时的最小量化间隔作为输入x轴的单位，那么各段落的起点电平分别是0、16、32、64、128、256、512、1024个量化单位。

编码步骤如下。

（1）对抽样值进行归一化：；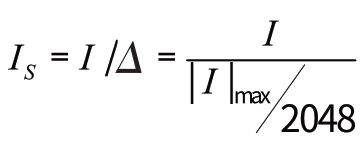

（2）根据的符号，确定；

（3）判断所在的段落范围，确定段落码；

（4）确定段内码：逐次比较归一化值与段内各量化区间的量化电平，得到；

（5）即为输出码字。

编码电平、解码电平（量化电平）及量化误差如下。

编码电平：

解码电平（量化电平）：

量化误差：

解码电平（量化电平）与的偏差，即。

例4　已知：抽样值为+631△，求按照A律13折线编码的8位码，以及编码电平、解码电平和解码量化误差。

采用三种方法进行求解。

（1）逐次比较法

第1次比较：抽样值Is=+631△，C1=1。(www.xing528.com)

第2次比较：串-并变化输出C2～C8为100 000 0，本地译码输出为

Is2=128△

Is=+631△＞Is2=128△，C2=1，位于第5段～第8段。

第3次比较：串-并变化输出C2～C8为110 0000，本地译码输出为

Is3=512△

Is=+631△＞Is3=512△，C3=1，位于第7段～第8段。

第4次比较：串-并变化输出C2～C8为111 0000，本地译码输出为

Is4=1024△

Is=+631△＜Is4=1024△，C4=0，位于第7段。

第5次比较：串-并变化输出C2～C8为110 1000，本地译码输出为

Is5=512△+[（1024△-512△）/16×8=768△

Is=+631△＜Is5=768△，C5=0。

第6次比较：串-并变化输出C2～C8为110 0100，本地译码输出为

Is6=512△+[（1024△-512△）/16×4=640△

Is=+631△＜Is6=640△，C6=0。

第7次比较：串-并变化输出C2～C8为110 0010，本地译码输出为

Is7=512△+[（1024△-512△）/16×2=576△

Is=+631△＞Is7=576△，C7=1。

第8次比较：串-并变化输出C2～C8为110 0011，本地译码输出为

Is8=512△+[（1024△-512△）/16×3=608△

Is=+631△＞Is8=608△，C8=1。

因此，编码C1C2C3C4C5C6C7C8为1110 0011，编码电平为608△，编码量化误差为631△-608△=23△。

（2）分别比较法

极性比较：抽样值Is=+631△，C1=1。

段落比较：512△＜+631△＜1024△，位于第7段，C2C3C4=110。

段内比较：631△-512△=119△＜256△，C5=0。

119△＜128△，C6=0。

119△＞64△，C7=1。

119△-64△=55△＞32△，C8=1

因此，编码C1C2C3C4C5C6C7C8为1110 0011，

编码电平=512△+（23×C5+22×C6+21×C7+20×C8）×[（1024-512）/16]△=608△，

编码量化误差为631△-608△=23△。

（3）除以量化间隔法

极性比较与段落比较可以采用逐次比较法或分别比较法，C1C2C3C4=1110。

段内比较：|抽样值-段落起始值|/量化间隔。

量化间隔=（1024-512）/16=32，

|631-512|/32，商为3，余数为23。

商转换为4位二进制，0011，所以C5C6C7C8为0011。

因此，编码C1C2C3C4C5C6C7C8为1110 0011，编码量化误差为余数23△。

4.MATLAB仿真实现

采用64位WIN7操作系统，matlab2012a进行仿真实现。算法采用方法（3），具体如下：

%确定段落码、量化间隔和起始电平

仿真结果如图2.4所示。

图2.4　Matlab仿真结果图

图2.4反映了PCM的抽样及量化过程。通过比较，量化后的折线可以近似原始模拟信号线，但是量化后的取值和抽样的原始值之间存在误差。

采用三种方法进行PCM编码，殊途同归，各种方法特点如下。

（1）逐次比较法，采用尝试策略，大于取1，否则取0，易于电路实现，思路简单。

（2）分别比较法，采用三步走策略，将极性、段落码和段内码分别进行比较，极性与0比较，段落码与各段起止电平进行比较。段内码采用逐次比较的方法，大于比较值取1，否则取0，分别比较，清晰明了。

（3）除以段内间隔法，极性与段落码的比较同方法（2），段内码采用除以段内间隔的方法，商转换为4位二进制编码。从本质上剖析了段内码的由来，计算过程简单，易于编程实现。