多维温度序列协同异常事件挖掘算法优化

气象事件的周期性行为揭示了气候的季节性或年际间的变化规律，因而从记载了气象信息的温度序列中挖掘气象事件引发了很多研究者的关注。在气象事件中，协同异常事件（co-anomaly）表现为相似的异常行为同时发生在不同的温度序列中，是气象研究中一类最重要的事件之一。协同异常事件对于理解气象变化以及分析异常事件的演化推移过程尤为重要。本小节介绍一个从多维温度序列中检测协同异常气象事件的方法。该方法首先把原始温度序列投影成符号式表达，然后通过统计显著性检验从中检测协同异常模式，最后从多维温度序列中生成可覆盖不同子维度以及不同子序列的协同异常事件。

为了更形象地理解什么是协同异常事件，图8-17展示了六条温度子序列，数据取自中国湖南省从12月13日到12月24日的六个气象站日均温真实数据。图8-17a展示了三条正常温度走势的子序列，图8-17b展示了三条子序列，它们的气温值异常的高于期望值。这里可以观察到，图8-17b中的三条子序列的异常走势极为相似，都属于同一个协同异常事件，它们很有可能是受到同一个气象因素的影响所致（比如同一股异常暖气流同时影响了这三个气象站）。因此找出并确定协同异常事件的所有影响成员（如所有属于同一个协同异常事件的温度序列）以及影响时间和演化方式，可以为进一步详细深入地探索研究特定气候现象提供预判和依据。比如，可以通过自动挖掘协同异常事件，帮助气象专家迅速确定一个同时发生在很多气象站的异常事件是偶尔会随概率发生的，还是概率上极其罕见的且具有进一步研究价值的事件。

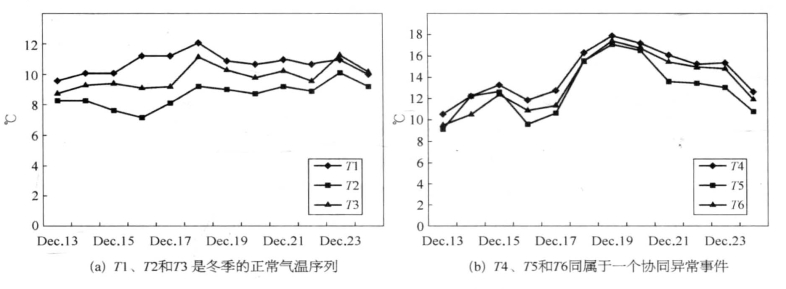
图8-17　采自不同气象站的六个温度序列的子序列（℃）

然而，从温度序列中挖掘气象协同异常事件存在很多技术上和领域上的挑战。首先，气象温度序列走势相对比较平滑，比如，与股票价格序列、车辆传感器序列相比要平滑很多，即温度序列的值通常来说不会偏离均值太远。因此，如果一些协同异常事件仅仅影响了一小部分地区，那对多维序列的平均值温度序列的影响甚微，难以用传统的异常检测的方法简单地从单维平均温度序列中检测出来。第二，与传统异常事件不同，相似的异常行为需要在一段时间内同时发生在若干数量的温度序列中，这样才能称为协同异常事件。然而，不能简单地使用频率计数（即统计被影响的温度序列的个数）来寻找值得注意的有趣的模式，因为在气象领域中的频繁模式常常代表了人人皆知的气候正常现象（比如冬暖夏凉，等等）。第三，协同异常气候事件通常随着时间在演化，因此在不同的时刻，被协同异常事件所影响的也可能随之改变，即协同异常事件常常关联着多维温度序列的不同子维度和不同子序列。例如，图8-18展示了一股冷空气在春季相邻的三天里自北往南的移动过程，大圆点为受此影响的地区。可以看到第一天受影响的地区（图8-18a中的大圆点）与第三天受影响的地区（图8-18c中的大圆点）很不一样。因为从温度序列中挖掘协同异常事件存在的这些困难，研究者和专家常常只能人工寻找和分析这些事件。然而，海量数据的日益累积以及分析的复杂性使得人工确定这些协同异常事件变得越来越困难。为了应对上述挑战，下面介绍协同异常事件监测框架Sevent。

图8-18　一个冷空气事件连续三天内从北往南在湖南省的影响地区（大圆点为影响到的地区）

具体来说，定义一个温度序列（temperature series） T = t1 ， t2 ， …， tn为一个由n个实数变量组成的有序序列，记录了随着时间变化的温度值，其中对象点（data point） t1 ，t2，…， tn以时间先后排序，并且时间间隔相等（比如，间隔一天）。接下来，定义温度序列数据集（temperature series data set） D是由m个温度序列组成的无序集合。温度序列T=t1 ， t2， … ， tn的子序列（subsequence） S是一个长度为k（k≤n）的自T的连续位置抽样，例如，S = tp，…， tp+k1—，其中1≤p≤n—k+1。

通常来说，为了从多维温度序列中检测协同异常事件，需要从温度序列数据集中确定子群体（sub-group）的行为。这里，简单的基于聚类的方法（比如，采用欧式距离进行高维子空间聚类）不太适合解决这一问题，原因如下：首先，在高维时间序列中搜索所有可能的子序列和子维度的时间复杂度非常高；第二，关注于寻找温度序列的群体异常行为，而非个体异常行为，也就是说，当仅仅观察协同异常事件中的一条子序列的走势时，它的行为相对于自身单维序列走势而言并不一定必须是异常的。

Sevent框架包含了三个主要步骤。首先，将温度序列转换成符号化表示，这样，每条温度序列的行为可以很容易地被各种字符的组合表示。然后，采用统计显著检验测试来找出协同异常模式。最后，相互关联的协同异常模式将被连接成协同异常事件。总的流程图如图8-19所示。

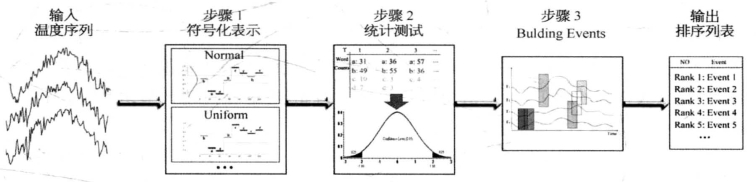
图8-19　Sevent框架流程图

1）符号化表示

时间序列符号化表示的通用框架包括下面三个步骤：首先，采用PAA［7］方法将原始时间序列降维；第二，生成一组分割点，通常从某个预先定义好的分布中抽取（比如均匀分布、高斯分布）；第三，通过比较PAA表示与分割点的位置，将他们映射成符号。

步骤一，温度序列T的PAA表示可以用= 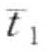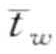， …， 来表示（子序列S的PAA表达相应的可以表示为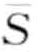= 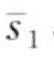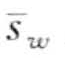，…， ）。具体来说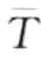，的第i个元素可以用下面公式计算，

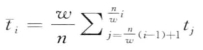
第二步，分割点可以从预先定义好的分布中抽取。这里需要预先定义字母表大小参数Ψ，该参数是用来决定表达字符的个数以及分割点的。由于大多数时间序列可以近似地拟合成正态分布或均匀分布，下面以这两种分布为例来描述生成分割点的方法。具体来说，正态分布的分割点的可以定义如下，这与SAX算法的分割点定义类似，

定义8.13［N（0，1）分布的分割点］：分割点是一个有序列表B= β1，… ，βΨ—1，其中在N（0，1）正态曲线下从βi 到βi+1的面积等于1/ψ（相应的，β0定义为—∞，βψ定义为∞）。

同样的，如果数据是从均匀分布中抽取，相应的分割点定义如下，

定义8.14（均匀分布的分割点）：分割点是一个有序列表B = β1， …， βΨ—1，其中βi+1—βi= （βψ—β0）/ψ（相应的，β0定义为数据集最小值，βψ定义为数据集最大值）。

值得指出的是，其他数据分布的分割点也可以用类似的方法定义。当得到一组分割点（B）后，可以把子序列投影成符号化表示，记做词。

定义8.15（词）：一个长度为k的子序列S可以如下表示成一个词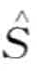=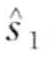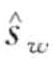， …， 。令αi记做第i个字母表的元素，例如α1 = a， α2 = b。那么从PAA表示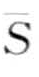到词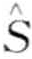的映射可定义如下，

举例来说，如果数据点的值在前两个分割点［β0，β1）之间，它将被映射成“a”，如果在［β1，β2）之间，它将被映射成“b”。

2）协同异常模式挖掘

在将原始温度序列转换成词后，可以计算每个时间戳上各个词的计数。不同的词代表了不同的行为，比如词“abcd”代表了一个温度逐渐上升的行为。因而通过统计同一个时间戳上各种不同行为（词）的个数，可以找出代表了群体行为的频繁模式（即频繁词）。然而，频繁并不能保证这个模式一定是值得人们注意的。正如同气象领域很多频繁模式（如冬暖夏凉等）是人人皆知的常识，并不值得引起关注。因此，考虑通过统计显著检验，来检验模式的重要性。具体来说，如下定义协同异常模式。

定义8.16（协同异常模式）：如果一个词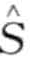=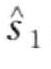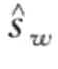，… ，的计数表现为统计显著性，则它是一个协同异常模式。

这里的“协同异常模式”与“异常模式”不同。如果只观察单条温度序列，协同异常模式的行为并不一定必须是异常的。只有当考虑一个群体的一致行为作为一个整体，并且他们的一致行为在历史上显现出异常显著性时，才称为协同异常模式。例如，每年，总有个零星几个城市在冬天会出现特别冷的气温。然而，如果某年的冬天大批城市都同时出现了一模一样的极度低温，那这就可能是一个协同异常事件，引发原因可能是同一股罕见的强劲寒冷气流所致。(www.xing528.com)

为了检测这些协同异常事件，定义一个零假设，并采用统计假设检验来计算每个观察到的词的P-value。

定义8.17：对一个给定的词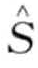和一个时间戳t，定义假设H0和H1：

H0 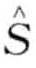： 在时间戳t是无趣的。

H1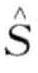：在时间戳t的频率显著大于期望值。

这里，每个词的期望值是从历史数据中学习，然后用来作为每个一致行为的基准值。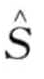的概率计算如下：

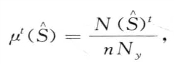
其中N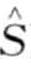（t）是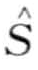在历史上所有年的时间戳t的计数总和，Ny是总年数，n是温度序列的条数。因此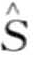的期望计数为：

然后，对于一个词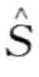的频率x，用正态逼近来计算它的P-value。即，N 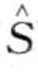（）t服从正态分布N 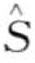（）t～N［nμ， nμ（1—μ）］。

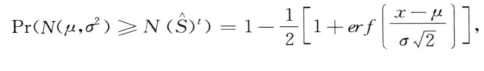
其中erf （x）是正态误差函数，具体定义如下：

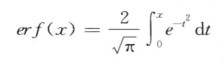
计算出来的P-value将和一个预定义的标准值α相比较。如果p＜α，那么H0假设将被拒绝，该词将被接受为协同异常模式。值得注意的是，这里还有其他的方法可以用来计算P-value，比如二项式检验、泊松近似等，它们都能用来检验一个词是否是统计显著的。

3）构建协同异常事件

邻近时间戳的协同异常模式，如果他们所关联的温度序列相同或相似，则很有可能属于同一个协同异常事件。这样，协同异常事件的时间跨度就不会局限于滑动窗口的宽度。这里需要定义一个阈值φ，如果两个邻近时间戳的协同异常模式的温度序列交集多于φ个，它们将被连接到一起。这样一来，由多个协同异常模式组成的协同异常事件则能够有长短不同的时间跨度。最后，提出一个打分函数Pscore来度量一个协同异常事件的罕见异常程度。通常来说，如果一个协同异常事件的Pscore高，则表明它是由较低的P-value的协同异常模式组成并且影响了非常多的温度序列。

协同异常事件的定义如下：

定义8.18（协同异常事件）：如果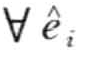∈E是一个协同异常模式，且，则是一个协同异常事件。

在这个定义下，协同异常事件可以看做是相关的显著词的簇，这些簇的时间跨度各异，且相关的显著词时间戳满足相邻并由公共的温度序列相连的条件。这里需要指出的是，一个协同异常事件中相邻时间戳上每个词所关联的温度序列并不需要是完全一致的。例如，图8-20展示了几种相关词构成协同异常事件的可能的方式。图8-20a展示了4个分散的词分别组成4个独立的事件。图8-20b展示了3个有着各自演化过程的事件。具体来说，图的左边展示了覆盖温度序列T3和T4跨越两个时间戳的事件。图的右边展示了一个从覆盖T3和T4、到覆盖T3和T2、再到覆盖T2和T1转移的事件，有可能是冷锋或台风事件自西向东的转移。注意到参数φ为时间戳相邻的词之间的最小公共温度序列，即如果两个词时间戳相邻，他们有多于φ的共同温度序列，那么他们就能被连接成候选事件。这样就可能存在多个下个时间戳的词满足于当前时间戳的某个词相连接。这种情况在现实生活中也是常见的，因为很多事件在随着时间展现出各种演化以及分化。故在连接阶段，针对这种分化的情形捕获并保留每一种事件演化方式。

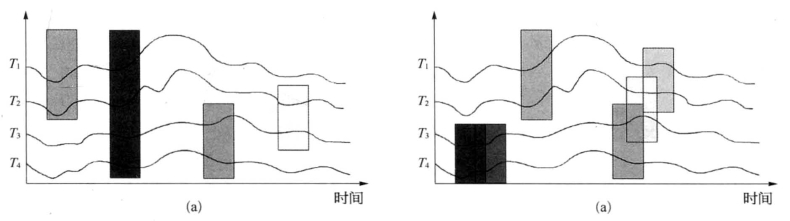
图8-20　相关的显著的词组成协同异常事件的各种方式

由于词的表达不同，时间跨度也不同，为事件构建全面的评估函数较为困难。一般来说，事件的协同异常程度与每个行为的罕见程度相关，也和他们的影响覆盖面相关。即行为发生的概率越低，那么就越罕见；覆盖程度越高，则越为严重。由于P-value是每个观察到的词的计数的概率，值域在0到1之间，因此添加—log于P-value上使得越为罕见的词更有一个更大的正值。这样，设计一个打分函数根据每个观察到的词的P-value以及影响到的温度序列的个数来评估每个事件。

定义8.19［打分函数Pscore（E）］：一个协同异常事件E，设RW（E）为E的相关的词S的集合，Pvalue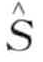（ ）为每个词的P-value值，Count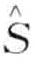（ ）为每个词所观察到的个数，E的总的打分函数值Pscore（E）定义如下：

总的来说，连接步包括下列三个步骤：首先，连接时间戳相邻且共享多于φ个公共温度序列的词；第二，重复迭代第一步知道没有新的连接添加；最后，用Pscore公式计算每个事件的打分值。

图8-21　Sevent伪代码

协同异常气象事件检测框架Sevent的伪代码展示在图8-21中。具体来说，伪代码第一行对应了温度序列的符号化表示（图8-18 Step 1）；伪代码第2—5行为统计检验（图8-18 Step 2）；伪代码第5—15行对应了建立事件的连接步（图8-18 Step 3）。

符号化表示的时间复杂度为O（m ·n），其中m是温度序列的条数，n是温度序列的长度。令ψ表示字母表大小，w为PAA元素个数，则计算P-value和连接词的时间复杂度为O（w ·ψ） +O（w·ψ）。即，Sevent总的时间复杂度为O（m ·n） +O（w·ψ）。