时间序列是常见的高维数据,直接对高维数据进行计算可能面临“维灾”问题。如何在降低时间序列的维度的同时保留其基本特征,一直以来是时间序列分析的一个挑战。
符号化表示(即将时间序列数据转换成离散的符号)是时间序列表示方法中重要的方法之一。符号化表示的优势在于可以允许采用很多已经发展成熟了的数据结构和索引(比如,后缀树、哈希、马尔科夫模型等)。
符号化聚集近似法(symbolic aggregate approximation, SAX)[4]是一种有效且流行的时间序列符号化表示算法,且很多基于SAX的后续改进算法也被提出。例如,iSAX[5]的提出使得SAX能扩展到大规模数据集。同样的,iSAX2.0[6]进一步被提出用于索引和挖掘巨大规模时间序列数据。
SAX旨在将实数值的时间序列转换成预设定的符号集,同时具有下界性质。下界性质能保证符号化表示后的对象距离恒小于等于原始数据的真实欧几里得距离。SAX的主要思想是,首先采用PAA (piecewise aggregate approximation)[7]方法将原始时间序列聚集,然后通过比较它们与分割点的位置,将他们映射到符号集。然而,SAX总是使用确定的分割点将时间序列映射成符号,这使得临近分割点的相似对象点难以被很好地表达。例如,图8-12展示了一条时间序列采用SAX算法符号化表示后的结果。其中参数设置字母表大小为5,图中的灰线为相应的4条分割线。从图中可以观察到第2~4个对象点,尽管欧式距离非常接近,仍被映射成不同的符号(ded)。同样的,第5~8个对象点也遭遇了同样的映射问题。事实上,导致这种问题的原因在于SAX的分割点(图中灰色线条)是由确定的值构成,这些值是从高斯分布提取。因此,当数据对象点的位置位于分割点附近时,无论他们的欧式距离有多么接近,他们将被映射到不同的符号。同时,这种情况还会给TLB(tightness of lower bound),即下界的紧度带来负面影响。直观来看,为了达到更好的映射结果和更紧的TLB界,可以增大字母表大小参数。然而,这将增大表示粒度,从而指数级地增加时间序列子序列分析时的候选符号组合,并可能引发过拟合问题。
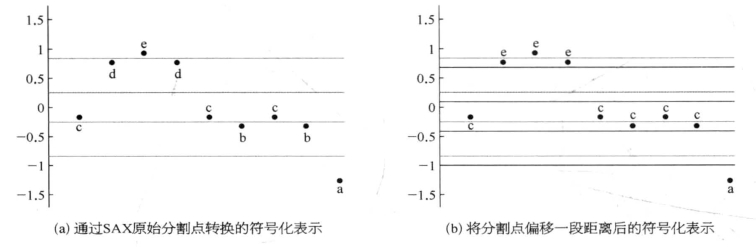
图8-12 一条时间序列中各对象点的符号化表示
然而,SAX和其他基于SAX的表示方法都采用确定的分割点(breakpoints)将时间序列映射成符号集,使得临近分割点的相似对象点难以被恰当地表达,并导致表示算法距离下界的紧度变差(即造成不佳的TLB界)。为了改进这种情形且减少由于确定分割点所导致的偏离,本章介绍一种基于随机偏移的符号化表示算法(random shifting based SAX,rSAX),该算法能在不增加表示粒度的前提下显著改善表示算法的TLB界,从而达到更好的映射结果和更紧的下界而无需增加字母表大小。
rSAX算法的关键思想是,通过随机偏移的方法生成一组随机分割点,而不是像SAX一样确定的分割点,即通过多次随机偏移分割点一段小距离来生成“软边界”而不是“硬边界”。这样,越为相似的对象点将有越高的概率被映射成同一个符号;相反的,越为相异的对象点将有更高的概率被映射成不同的符号。
例如,图8-12b展示了当采用rSAX方法后的时间序列符号化表示,其中分割点被随机偏移了一段较小距离。可以观察到,第2~4个对象点都表示成同一个符号“e”,第5~8个对象点都被表示成同一个符号“c”。
下面介绍算法所必需的一些相关定义和概念。为了易于理解,相关的数据符号表达在表8-6中展示。
表8-6 数据符号表

具体来说,定义时间序列(time series) T = t1 , t2 , …, tn为一个由n个实数变量组成的有序序列,其中对象点(data point) t1 , t2, …, tn以时间先后排序,并且时间间隔相等。事实上,每条时间序列记录了一个事物对象(object)随着时间推移的一系列观察值。接下来定义时间序列数据集(time series data set) D是由m个时间序列组成的无序集合。时间序列T=t1, t2, … , tn的子序列(subsequence) S是一个长度为k( k ≤ n)的自T的连续位置抽样,例如,S = tp,… , tp+k—1,其中1≤p≤n—k+ 1。
为了降低原始时间序列数据的维度,SAX和rSAX算法均采用了PAA,即分段聚集近似法来把原始时间序列转换成一个聚集离散的表达,可以用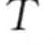 =
=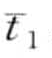 ,…,
,…, 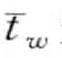 来表示(子序列S的PAA表达相应的可以表示为
来表示(子序列S的PAA表达相应的可以表示为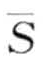 =
=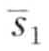 ,…,
,…, 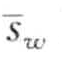 )。即
)。即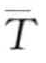 的第i个元素可以用下面公式计算:
的第i个元素可以用下面公式计算:
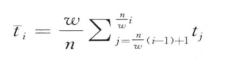
同样的,SAX和rSAX需要预先定义字母表大小参数Ψ,该参数是用来决定表达字符的个数以及分割点(breakpoints)。分割点定义如下[4]:
定义8.10(分割点):分割点是一个有序列表B = β1,…,βΨ1—,其中在N(0,1)高斯曲线下从βi到βi+1的面积等于1/ψ(相应的,β0定义为—∞,βψ定义为∞)。
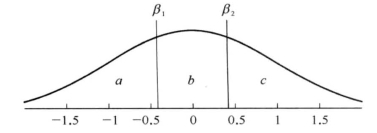
图8-13 分割点的示例(字母表大小Ψ=3)
举例来说,图8-13展示了当Ψ=3时的分割点分布位置。分割位置β1和β2将N(0,1)高斯曲线下的面积平均分成三等份,对应图中的面积a,面积b和面积c。时间序列中的对象点落入某个面积将被相应的符号(a或b或c)表示。
一旦确定了分割点,一个子序列可以被映射到符号,该符号可以定义为一个词(word)。具体来说,词可以定义如下:
定义8.11(词):一个长度为k的子序列S可以如下表示成一个词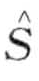 =
= 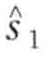 , … ,
, … , 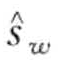 。令αi记做第i个字母表的元素,例如α1 = a, α2 = b,那么从PAA表示
。令αi记做第i个字母表的元素,例如α1 = a, α2 = b,那么从PAA表示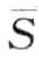 到词
到词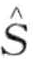 的映射可定义如下,
的映射可定义如下,
![]()
同时,SAX定义了MINDIST函数,能够返回原始时间序列的两个词Q= { q 1 , …, qw}和C= {c1,…,cw}的最小距离,定义如下,
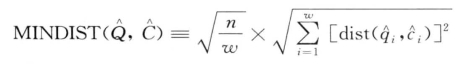
其中n是原始时间序列的长度,w是PAA元素的个数。dist(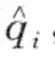 ,
, 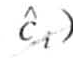 )为距离函数,当
)为距离函数,当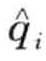 和
和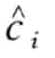 为相邻字符时(比如a和b则为相邻字符),dist(
为相邻字符时(比如a和b则为相邻字符),dist(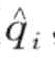 ,
, 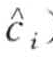 ) = 0;否则,dist(
) = 0;否则,dist(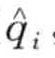 ,
,  )的值等于两个字符之间最远分割点之间的欧式距离(例如图8-13中字符a与c的dist距离为0.86)。
)的值等于两个字符之间最远分割点之间的欧式距离(例如图8-13中字符a与c的dist距离为0.86)。
基于MINDIST,可以定义一个度量来计算下界的紧度,计算方法为用下界距离比上实际的欧式距离,定义如下,

TLB是一个非常重要的时间序列表示算法的标准度量方法,常用于比较各个时间序列表示算法的性能[8]。
下面首先详细介绍提出的rSAX算法,然后在理论上证明rSAX能达到比SAX更好的映射性能和更佳的TLB。
在设计表示算法时,考虑两种最佳状况:完美映射,相似的对象点都能被映射到同一个字符;紧的界,近似的下界距离越接近真实欧氏距离越好。SAX是时间序列表示算法中最流行的算法之一。然而,当两个对象点碰巧分布在一个分割点的两边时,无论这两个点距离有多么的接近他们都将被映射成不同的字符。
具体地,rSAX的伪代码详如图8-14所示。

图8-14 rSAX的伪代码
rSAX算法的时间复杂度为O(m·n)+O(m·w·τ),其中m为时间序列的个数,n为时间序列的长度,w为单个时间序列PAA长度,τ为随机偏移的次数。
观察一个对象点(或一个PAA表示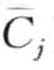 )tj ∈ T, 1≤j≤| T。令αk为字母表第k个元素,字母表大小为ψ, tj的SAX表示为αk当且仅当βk—1 ≤ tj <βk。令d为所有两两分割点的最小距离,令li为从范围为
)tj ∈ T, 1≤j≤| T。令αk为字母表第k个元素,字母表大小为ψ, tj的SAX表示为αk当且仅当βk—1 ≤ tj <βk。令d为所有两两分割点的最小距离,令li为从范围为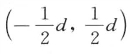 的均匀抽样生成的随机变量,随机偏移后的分割点变为βk = βk + li。生成τ一1组随机扰动,并将每个li ∈ {l1 ,…, lτ—1}扰动值加到初始的分割点上,而不是像SAX一样使用固定不变的分割点。原始时间序列则被映射到符号集一共τ次,也就是说,为原始时间序列数据集生成了τ个版本的符号表示。
的均匀抽样生成的随机变量,随机偏移后的分割点变为βk = βk + li。生成τ一1组随机扰动,并将每个li ∈ {l1 ,…, lτ—1}扰动值加到初始的分割点上,而不是像SAX一样使用固定不变的分割点。原始时间序列则被映射到符号集一共τ次,也就是说,为原始时间序列数据集生成了τ个版本的符号表示。
图8-15显示了一个rSAX的实例。字母表大小ψ=4,相对应的分割点为B ={—0.67, 0,0.67}。图8-15a为标准SAX的表示结果,时间序列PAA近似(T= 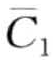 ,
, 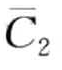 ,
,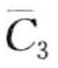 ,
, 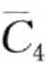 )映射成词cbbc。观察到
)映射成词cbbc。观察到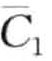 和
和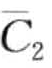 非常接近,但碰巧被分割点0分开而被两个不同字符表示;
非常接近,但碰巧被分割点0分开而被两个不同字符表示;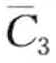 和
和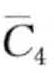 相隔较远,然而MINDIST(
相隔较远,然而MINDIST(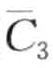 ,
, 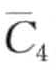 ) = MINDIST(b,c)=0[4]。图8-15b展示了一次随机偏移的结果。令li为一个从(—0.335, 0.335)均匀分布生成的随机变量,则分割点偏移成B={—0.67+li, 0 +li, 0.67+li} 。在这次偏移中,
) = MINDIST(b,c)=0[4]。图8-15b展示了一次随机偏移的结果。令li为一个从(—0.335, 0.335)均匀分布生成的随机变量,则分割点偏移成B={—0.67+li, 0 +li, 0.67+li} 。在这次偏移中,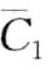 和
和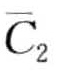 映射到同一个字符b,且MINDIST(
映射到同一个字符b,且MINDIST( ,
, 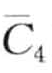 ) = MINDIST(a, c) = 0.67。图8-15c展示了另一次偏移结果,偏移量为li+1。同样的,
) = MINDIST(a, c) = 0.67。图8-15c展示了另一次偏移结果,偏移量为li+1。同样的,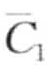 和
和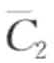 映射到同一个字符c,且MINDIST(
映射到同一个字符c,且MINDIST(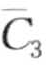 ,
, 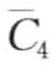 ) =MINDIST(b, d) = 0.67。(https://www.xing528.com)
) =MINDIST(b, d) = 0.67。(https://www.xing528.com)
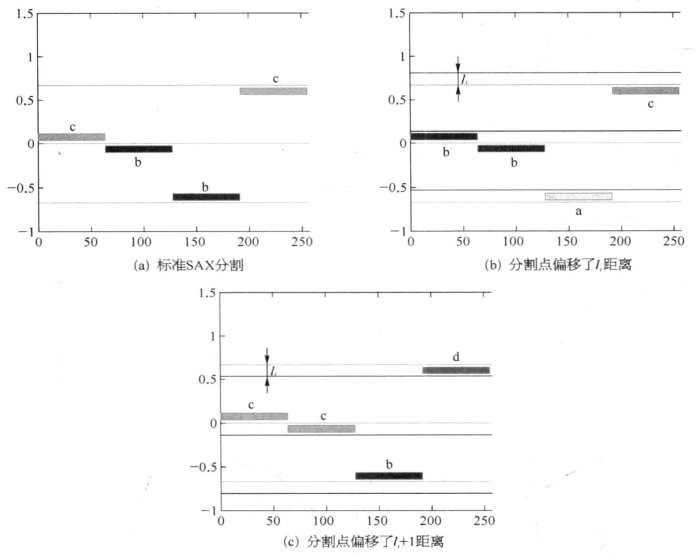
图8-15 rSAX表示示例
1) rSAX的映射性质
一个对象点tj的表示符号将发生改变如果它满足下列两个条件之一:βk+li ≤tj <βk,其中—0.5d < li < 0; βk—1 ≤ tj <βk—1 + li,其中0<li <0.5d。图8-16a展示了当li = 0.1时可变区间的一个示例。位于深蓝色较窄区间内的对象点的表示符号会发生改变,从αk改变到αk—1;位于灰色较宽区间内的对象点的表示符号保持不变。图8-16b展示了τ次随机偏移时所有可能的可变区间(深蓝色区间)。位于灰色区间的数据点的表示符号保持不变。

图8-16 rSAX的可变与非可变区间(字母表大小ψ=6)
对于一个对象点tj,如果(βk—1 +βk)/2 ≤ tj < βk,它的表示符号可能会从αk改变到αk+1。令pchange为tj表示为α k+1的概率,则pchange = (tj+0.5d—βk)/d,其中d是所有两两相邻分割点的最小距离。如果βk—βk —1=d, tj总有概率被α k+1表达。因为(βk—1 +βk)/2≤tj <βk, max(pchange) = 0.5, min(pchange) = (βk—1—βk)/2l+0.5≥ 0。因此0 ≤ pchange < 0.5 。
如果βk ≤tj < (βk—1 +βk)/2,在随机偏移的过程中它的表示符号可能会从αk改变到αk—1。同样的可以计算tj表示成αk—1的概率:pchange = βk-1—tj + 0.5d/d, 0 ≤ pchange < 0.5。
定理8.1:令tj和t j+1 = tj +ε为数据集中两个对象点,0<ε<d。当0<ε≤0.5d时,tj和tj+1在τ次抽样过程中被同一个字符表示的频率小于等于0.5的概率为![]() 当0.5d<ε<d时,tj和tj+1在τ次随机偏移过程中被同一个字符表示的频率大于等于0.5的概率为
当0.5d<ε<d时,tj和tj+1在τ次随机偏移过程中被同一个字符表示的频率大于等于0.5的概率为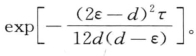
证明:令X1 , …, Xτ为独立伯努利试验。Pr[Xi=1]=psame=(d-ε)/d,代表tj和tj+1在一次随机偏移过程中被同一个字符表示。Pr[Xi = 0]=pdif = ε/d,代表tj和tj+1在一次随机偏移过程中被不同字符表示(1≤i≤τ)。令![]() 为τ次随机偏移中ti和tj+1被同样字符表示的次数。x服从二项分布。
为τ次随机偏移中ti和tj+1被同样字符表示的次数。x服从二项分布。![]() 。使用契尔诺夫界,对所有0 <δ≤1,
。使用契尔诺夫界,对所有0 <δ≤1,
![]()
![]()
令fsame为tj和tj+1在样本被同一个字符表示的频率,则![]() 为样本中同样映射的个数。这里E[Cs]= psame·τ,则可以得到,
为样本中同样映射的个数。这里E[Cs]= psame·τ,则可以得到,
![]()
用契尔诺夫界代入不等式8-26,对于所有的0<δ≤1得到,
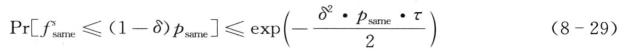
同样的,对于所有的0<δ<1得到,
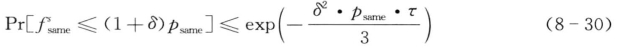
对于0<ε≤0.5d, 0.5 ≤psame = (d—ε)/d < 1。通过将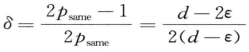 代入公式(8-28),得到,
代入公式(8-28),得到,
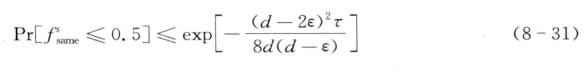
对于0.5d<ε<d,0<psame =(d—ε)/d<0.5。通过将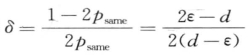 代入公式(8-30),得到,
代入公式(8-30),得到,
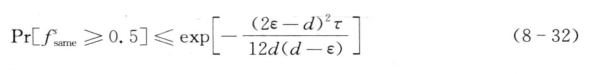
定理8.1得证。
当增大τ时,概率的上界将变小。很容易从两两映射关系性质扩展到所有的对象点。也就是说,当τ增大时,相似的对象点被映射到同样符号的概率也会更大。
契尔诺夫界描述了随机变量的尾部分布,并且为随机变量偏离期望的概率给出了界。令c为这个概率。则1—δ描述了样本的准确度,1—c描述了样本的置信度。可以得到,
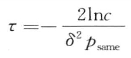
当增大τ时,样本的置信度也会增加,这意味着样本的近似的相似度(即是否被同一个字符表示)能很好地代表整体的相似度。
2) rSAX的下界性质
与SAX算法的MINDIST类似,rSAX也有自己的下界距离度量。rSAX的最小距离定义如下。
定义8.12( rMinDist) : rSAX的两两对象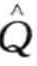
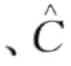 的最小距离(rMinDist)是所有τ个版本的SAX表示的最大距离的和。
的最小距离(rMinDist)是所有τ个版本的SAX表示的最大距离的和。
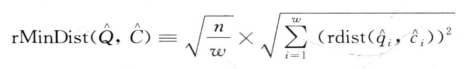
![]()
rSAX的过程包括一次SAX以及τ—1次的随机偏移过程。对于任意对象点qi和ci,rSAX选取所有τ个距离中的最大值作为最紧的下界距离。容易看出,
![]()
因此rSAX的TLB为,
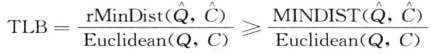
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




