如果两个时间序列有足够多的不重叠的按时间排序的子序列对是相似的，那么可以认为这两个时间序列是相似的。基于的思想是其中一条在决定其子序列是否与另一条序列的子序列匹配前，可以经过合适的变换。
在给出算法之前，先给出一些相关符号说明：
（ S = （st | t = 0，1，2，…， n—1）表示一个长度为n的时间序列，是一个有序集。
② Len（S）表示序列S的长度。
③ First（S）表示序列S的第一个元素。
④ Last（S）表示序列S的最后一个元素。
⑤ S［i］表示S的第i个元素。
⑥ S［i，j］表示由元素i到j组成的S的子序列，子序列S［i，j］的长度是j—i+1。
⑦序列上元素之间的“＜”关系表示在序列S上，如果i ＜ j，那么S［i］＜ S［j］。
⑧Ss表示S的子序列，如果序列S有k个子序列，则这些子序列表示为：Ss1 ，Ss2 ， … ， Ssk 。
⑨子序列间的“＜”关系表示若First（Ssi） ＜ First（Ssj ），则称Ssi ＜Ssj。
定义8.4（子序列重叠）：假定Ssi、Ssj为S的子序列，若First（Ssi） ≤ First（Ssj ）≤Last（ Ssi）或First（Ssj） ≤ First（Ssi ）≤Last（Ssj ）成立，则SsiS、sj重叠。
上一小节已给出序列相似的定义，即如果两个时间序列S和T，分别包含无重复的子序列Ss1，Ss2，…，Ssm和Ts1 ， Ts2 ， … ， Tsm满足以下条件：
① Ssi ＜ Ssj且Tsi＜Tsj，1≤i＜j≤m。
②3某一个比例系数λ和某一个转换变量θ满足
其中，≈是子序列相似操作符，θ（λ（Ssi））表示子序列Ssi经过转换λ和θ后的形式；
两个序列的匹配长度与总长度之比必须超过阈值ξ；
那么序列S和T被认为是ξ相似的。
定义8.5（ 子序列相似）：如果两个子序列满足以下条件：
①其中一个子序列在另一个子序列的指定宽度ε范围内。
②匹配的原子单元是长度为ω（一个窗口大小）不包含异常点的子序列。匹配一个窗口后，长度为Υ（最大为gap）的子序列可被忽略。
那么两个子序列相似。
定义8.6（ 序列S的Υ-投影SΥ）：如果序列SΥ满足以下两个条件：
①SΥ中的所有元素也在S中，并且有相同的顺序。
②如果S［i］和S［j］是S中对应SΥ中的两个连续元素SΥ ［k］和SΥ［k+1］，那么j—i ≤ Υ。
则称SΥ为序列S的Υ-投影：
定义8.7［序列S的（ω， Υ）-投影Sω，Υ］：如果序列Sω，Υ满足下面条件：
①Sω，Υ是S的Υ-投影。
②如果Sω，Υ［i］和Sω，Υ［i+1］在S中的对应元素不连续，那么S的元素Sω，Υ［i—ω+1］…Sω，Υ［i—1］是连续的。
则称Sω，Υ是序列S的（ω，Υ）-投影（图8-9）。
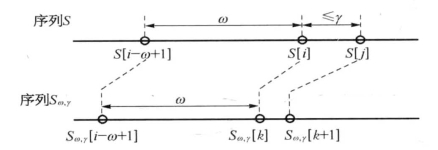
图8-9 （ω，Υ）-投影
定义8.8［（ ε， ω， Υ）-相似］：如果存在（ω， Υ）-投影π1，π2满足
则子序列S和T是（ε，ω，Υ）-相似，记为S≈T。
以上是关于子序列相似的一些定义和说明，下面给出判断两个序列S和T是否相似问题的解决方法，该方法将问题分为三个子问题：原子匹配、窗口缝合以及子序列排序。
1）原子匹配（Atomic Matching）
原子匹配目的是在S和T中找出所有无间隙的长度为ω（称为窗口）的相似的窗口对。
考虑到幅度调整和平移变换，采用滑动窗口技术：用长为ω的窗口，从头到尾扫描整个序列，得到其上所有的长为ω的子序列，即原子序列。
然后将原子序列标准化，方法是使用公式
将原子序列(www.xing528.com)
w映射到（—1，+1）区间，得到一个新原子序列w′。其中W max和Wmin分别是窗口w中最大值点和最小值点。
定义8.9（原子序列相似）：两个标准化后的原子序列
，如果满足：
，则称原子序列
和
是ε-相似的，简称为原子序列相似。
标准化后的原子序列可以看作是ω维空间上的一个点，于是原子匹配问题转换为：给定ω维空间中的点的集合，找出相互间距离在ε内的所有点对，这里距离度量定义使用Loc标准度量（见第2章聚类分析）。算法使用多维索引结构（如R+-树）存储所有的点，再采用一个self-join的算法发现索引树中所有的相似点对。原子匹配阶段最终找出所有相似的原子。
2）窗口缝合（Window Stitching）
窗口缝合的主要任务是将相似的原子序列拼接起来，形成比较长且彼此相似的子序列。
窗口缝合技术中允许在原子匹配间有间隙gap，因此可以把一些噪声数据和两个序列上有差异但在相似性比较时可以忽略的部分过滤掉。
设S1 ， …， Sm和T1 ， …， Tm分别为S与T上m个规范化后的原子，且对于任意i，都有Si与Ti相似，另外对于任何j ＞ i， First（Swi） ≤First（Swj ），First（Twi） ≤First（Twj ）。
若满足下面两个条件，则可缝合S1 ，…， Sm和T1，… ，Tm，使它们形成一个相似的子序列：
（1）对任何i＞1，如果Si不与Si-1重叠，且Si与Si-1之间的gap小于等于γ，同时T也满足这个条件；或者，如果Si与Si-1重叠，重叠长度为d， Ti与Ti—1也重叠，且重叠长度也为d。
（2） S上的每个窗口进行规范化时候，所用的比例因子大致相同，T上的每个窗口进行规范化时所用的比例因子也大致相同。
例8.10：有S和T两个序列，在原子序列匹配过程中，得到三个相似的原子对（S1，T1）、（S2，T2）、（S3，T3），并且满足上述窗口缝合条件，可以把它们缝合起来得到一对相似的子序列。图8-10表示窗口缝合的过程。
图8-10 窗口缝合可能情况图解
①有重叠的情况：原子S1与S2重叠，重叠长度为d， T1与T2也重叠，重叠长度也为d，满足条件（1）及窗口缝合其他条件，由此可以把S1与S2缝合，T1与T2缝合。
②不重叠的情况：原子S2与S3不重叠，两者之间有一个长度不大于γ的gap，满足条件（1）及窗口缝合其他条件，可以把S2与S3缝合，T2与T3也缝合。
最后的缝合过程对相似的原子对（S1， T1 ）、 （S2， T2）、 （S3， T3）缝合结果图8-10所示。
窗口缝合步骤的主要思路是将窗口缝合问题看成是一个无环图中查找最长路径的问题，最终输出每个S和T序列对的匹配窗口对。
首先，按以下方式构造每个S和T序列对的匹配图G：
（1）每个顶点表示每对匹配窗口。
（2）从Mi=（Si， Ti）的顶点到Mj=（Sj，Tj）的顶点画一条边，当且仅当
①Mj中的窗口的起始点都在Mi窗口中的起始点之后，即
first（Si） ＜ first（Sj） first（Ti） ＜ first（Tj）
②下面任何一种情况成立：
a.两个匹配窗口不重叠且间隙小于等于Υ，即
（Si∩Sj = Ti∩Tj = Φ） ∧ （first（Sj）—last（Si） ≤ Υ） ∧ （first（Tj）—last（ Ti） ≤Υ）
b.在S中Sj和Si重叠的数量与在T中Tj和Ti重叠数量相同
（3）边Mi→Mj置标号＜lij， fs i，lsj， fti， ltj ＞，其中，fsi = first（Si），lsj = last（Sj），fti = first（Ti），l tj = last（ Tj）且lij = （lsj—fsi）+（ltj—ftj ）
边lij的长度表示总匹配长度（包括间隙）。
图8-11显示了A，…， E的窗口缝合对的相应图。因为最大间隙限制不满足，所以图中没有边A→E。同样的，由于B、F是具有不同重叠长度的重叠窗口，所以B→F无边。
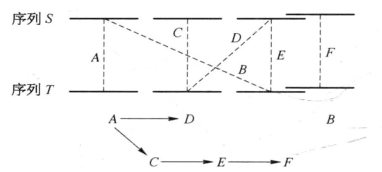
图8-11 匹配图
考虑图G中的一条路径P+A被具有边A的路径包含，假设P和A的标号分别是＜lij， fsi， lsj， fti， ltj＞和＜l′ij ， fs′i， ls′j， ft′i， lt′j＞，则定义P+A的标号为：＜ ［（ls′jf—si） + （ltj—fti）］， fsi， ls′j ， fti， lt′j＞，由此G具有以下性质：
如果图G中的两条路径P， Q， length（P）＜length（Q）且first（P） =first（ Q），那么对G中的任何一条边R，有length（P+R）＜length（ Q+R ）。根据这个性质，可以找到相应的最长匹配。
3）子序列排序（Subsequence Ordering）
子序列排序的主要任务是，找到具有最长匹配长度的非重叠的子序列匹配排序。
设S = （S1， T1）（^Sk， Tk）是经过原子序列匹配和窗口缝合步骤后得到的k个S和T的子序列对，可以得到满足以下条件的S的一个子集（Sl1 ，Tl1）…（Slm， Tlm）：
（1） Sli＜ Slj 且Tli＜Tlj，1≤i＜j≤m。
（2）用于每一个Sli匹配的比例因子大致相同，用于每一个Tli匹配的比例因子也大致相同。
（3）该子集的总匹配长度是S中最大的。即
大于等于S任何其他子集的匹配长度。
通过前面的步骤已经找到了相似的子序列对，之后可对窗口缝合算法进行一些细微改变用以判断两个子序列的最大长度匹配。
在该步中再次形成匹配图，并在匹配图中寻找最长的路径。在序列S和T的匹配图中，对于Mi=（Si， Ti）和Mj=（Sj， Tj），当且仅当last（ Si） ＜ first（ Sj）且last（ Ti） ＜first（Tj）成立则生成一条从Mi到Mj的边。边的长度是四个子序列Si， Sj， T和Tj的长度和。
子序列排序过程常与窗口缝合步骤合为一步，在此为了更加清晰的说明问题将两者分开描述。有时候，并不需要子序列排序而仅需窗口缝合步骤即可满足特定应用的需求。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
