基于密度的异常分析算法优化

基于距离的异常的定义只能检测到某些异常，因为这个定义从全局来看数据集，这些异常也就被看作全局的异常。但是对许多现实数据集而言，它们存在非常复杂的结构，很难用一个全局参数来得到所有有意义的异常，即还存在其他类的异常——相对于它们的局部邻域（特别是相对于它们的邻域的密度）的异常。这些异常被认为是“局部”（local）异常。

下面用一个例子来解释这类局部的异常（图6-8）。

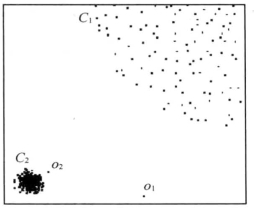
图6-8　全局参数异常的缺陷

例6.1：一个含有502个对象的简单二维数据集D。其中，400个对象属于第一个簇C1，100个对象属于第二个簇C2，还有两个额外的对象o1 、o2。在这个例子中，C2所形成的簇的密度高于C1，根据Hawkins的异常定义（异常是数据集中偏差较大的数据，它们的产生机制可能不同于其他数据），o1和o2都被认为是异常，但C1和C2中的对象则认为它们不是异常。但是根据基于距离的DB（pct， d）-异常定义，只有o1是一个“合理”的DB（pct， d）-异常。因为如果C1中的每一个对象q与它的最近邻居的距离大于o2和C2的距离，即d（o2，C2），那么可以断定没有合适的pct和d，使得o2是DB（pct，d）-异常，而C1中的对象不是。

原因如下，如果d的值小于d（o2， C2），则所有501个对象（pct= 100×501/502）到o2的距离都大于d，但是同样的结果也出现在C1中的任一个对象q上。因此，o2和C1中所有的对象都是DB（pct， d）-异常。

否则，如果d的值大于d（o 2，C2），那么显然有：如果o2是一个DB（pct， d）-异常，那么C1中的许多对象q也是DB（pct， d）-异常。这是因为集合｛p ∈ D | d（p，o2） ≤d｝的基数总是大于集合｛p∈D|d（p，q）≤d｝的基数。因此，如果o2是一个DB（pct，d）-异常，那么C1中的许多对象q同样也是DB（pct， d）异常。更坏的情形是，这里存在pct和d的值使得o2不是异常，而C1中的某些对象q却成为异常。

1）局部异常的形式化定义

以上的例子表明，从全局角度考察DB（pct，d）-异常，在某些情况下是有意义和充分的，但是通常情况下簇的密度是不同的，当各种密度的簇存在时，这种方法将不再适用。与前述异常定义不同，这里的异常不被认为是二元性质，而是为每一个对象指定一个异常因子（outlier factor），以此作为这个对象被判断是否为异常的度量。

符号说明及定义：

①D：表示数据集。

②o， p， q：表示数据集中的对象。

③ d（p， q）：表示对象p， q之间的距离。

④C：表示一组对象（有时C形成一个簇）。

⑤ d（p， C）：表示p和C中的对象q之间的最小距离，即d（p， C） = min｛d（p， q） | q ∈ C｝

定义6.9［对象p的k-距离，k-distance（p）］：对于任意正整数k，定义对象p的k-距离为p和某个对象o（o ∈ D）之间的距离d（p，o），并且这里的o满足：

①至少存在k个对象o′，使得d（p， o′） ≤ d（p， o），其中o′∈D\｛p｝。

②至多存在k—1个对象o′，使得d（p， o′） ＜d（p， o），其中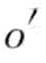∈D\｛p｝′

定义6.10［对象p的k-距离邻域，Nk-distanc（ep） （p）］：给定p的k-距离k-distance（p） ，p的k-距离邻域包含所有与p的距离不超过k-distance（p）的对象，即Nk-distance（p）（p）=｛q ∈D\｛p｝ | d（p，q） ≤k-distance（p） ｝，这些对象q称为p的k-最近邻域（k-nearest neighbors）。简单起见，用Nk（p）表示Nk-distanc（ep）（p） 。

注意在定义6.9中，k-distance（p ）能够适用于任何正整数k，尽管对象o可能并不唯一。此时，Nk（p）的基数大于k。假设有：1个到p为1个距离单位的对象；2个到p为2个距离单位的对象；3个到p为3个距离单位的对象。那么，2-distance（p）与3-distance（p）是一样的，并且有3个到p为4-distance（p）的对象，此时，N4 （p）的基数等于6，而不是4。

定义6.11［对象p相对于o的可达距离，reach-distk（p， o）］：给定自然数k，对象p相对于对象o的可达距离定义为：reach-distk（p， o） = max｛k-distance（o），d（p， o） ｝ 。

图6-9给出了k=4时对可达距离的描述。如果对象p距离o较远（例如p2），则用两者之间的实际距离作为可达距离；如果它们距离很近（例如p1），则用对象o的k-距离替代它们的实际距离。这样做使得那些靠近o的对象p到它的距离d（ p， o）不会变化太大，参数k用于控制平滑的效果。k值越大，具有相同邻居的对象越可能有相近的可达距离。

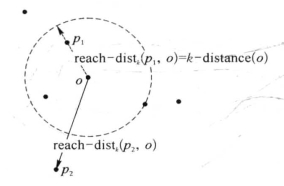
图6-9　reach-dist（p1，o）和reach-dist（p2，o），k=4

在典型的基于密度的聚类算法中，大都使用了两个参数对密度进行定义：

①参数MintPts表示对象的最少数目。

②另一个参数表示容量（volume）

这两个参数定义了聚类算法的密度阈值。如果某些对象或区域的邻居密度超出了某个给定的阈值，则认为它们是相互连接的。要检测基于密度的异常，必须比较不同对象集合之间的密度，必须动态地确定这些对象的密度。因此，将MinPts作为唯一的参数，并且使用reach-distMinPts（p，o）、o∈NMinPt（sp），作为确定对象p邻居的密度的一个度量。

给出了以上定义后，下面给出局部异常因子（local outlier factor， LOF）的定义。

定义6.12［对象p的局部可达密度，l rdMinPs（p）］：对象p的可达密度定义为：

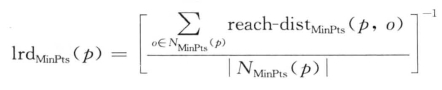
也即，对象p的局部可达密度是对象p与它的MinPts-邻域（MinPts-nearnest neighbors）的平均可达距离的倒数。当所有可达距离的和为0时，局部密度将会接近∞。（如果至少有MinPts个对象不同于p，但它们具有相同的空间坐标时，即数据集中p至少有MinPts个重复值，则会出现上述情形。）在此假设不会出现重复值，所以不必进行处理。（如果要处理重复值，可以提出k-唯一距离邻居的概念，它与定义6.9中k-距离的概念类似，只需要添加一个条件，要求至少k个对象具有不同的空间坐标）。

定义6.13［对象p的局部异常因子，LOFMi Pts （p）］：对象p的局部异常因子定义为：

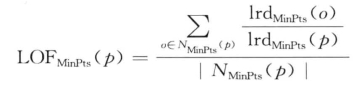
对象p的异常因子能够描述对象p的异常程度，它是p的MinPts-邻域与p的局部可达密度的比值。从定义可知，如果p的局部可达密度越低，p的MinPts-邻域的局部可达密度越高，则p的局部异常因子的值越大，就更可能认为它为异常；反之则可能性小。为简明起见，使用reach-dist、lrd和LOF分别表示reach-distMinPts（p， o） 、 lrdnPtMis（ p）和LOFMinPts（p） 。

2）局部异常因子的性质
下面给出局部异常因子的性质，分析局部异常因子与所期望的异常的联系。首先是对簇中对象的异常因子的讨论，并证明这些对象的局部异常因子接近于1；另外给出任意对象的局部异常因子的上下界；并考虑这个界是否是紧致的；最后讨论哪些邻域属于重叠的多个簇的对象的局部异常因子的界。

引理6.1：令C为一个对象集合，reach-dist-min表示C中对象间的最小可达距离，即reach-dist-min=min｛reach-dist（p， q） | p， q ∈C｝；类似的，reach-dist-max表示C中对象的最大可达距离；ε定义为（reach-dist-max/reach-dist-min）—1。那么对所有满足以下条件C中的对象p：

① p的所有MinPts-邻域中的对象q都在C中。

②q的所有MinPts -邻域中的对象o也都在C中。

下式成立：1/（1 +ε） ≤ LOF（p） ≤ （1 +ε）

证明：由①以及reach-distMinPts（ p， q）的定义，对p的MinPts-邻域中对象q，有：reachdist-min≤reach-distMinPts（ p， q） ≤reach-dist-max

因此，

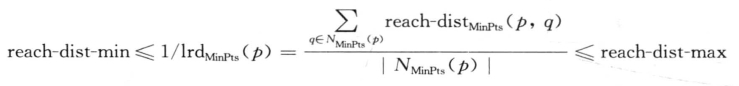
另外有②和reach-distMinPs （q，o）的定义，对q的MinPts-邻域中的对象o，有：

reach-dist-min≤reach-distMiPs（q，o） ≤reach-dist-max

因此，

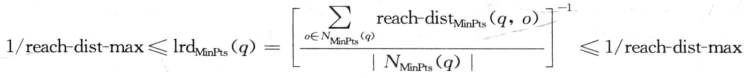
所以，对象p的局部异常因子满足：

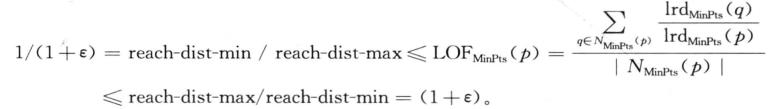
引理6.1说明簇内靠近核心点的对象的LOF接近于1，不应该被认为是局部异常。对于那些处于簇的边缘或是簇的外面的对象，如图6-9中的对象o1，下面的定理6.1回答了这些问题，给出了任意对象p的LOF值的上下界。

3）对象p的LOF值的上下界

对任意对象p，记directmin （p）为p相对于p的MinPts-邻域中点的最小可达距离，即：

同样，directmax （p）为p相对于p的MinPts-邻域中点的最大可达距离，即：

另外，推广这些定义到p的MinPts-邻域上的点q，记indirectmin（p）为q相对于q的MinPts-邻域的最小可达距离，即：

indirectmin （p） = min｛ reach-distMinPts （q， o） | q ∈ NminPts （p）且o∈NminPts（q）｝

同样，indirectmax （p）表示q相对于q的MinPts-邻域的最大可达距离，即：

indirectmax （p） = max｛ reach-di stMinPts（q， o） | q ∈ NminPts（p）且o∈ NmminPts （q） ｝(www.xing528.com)

定理6.1：令p是数据集D中的一个对象，且1 ≤ MinPts ≤ | D |，那么有如下不等式成立：

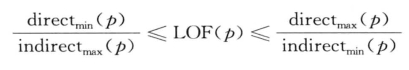
证明： （a）先证左边的不等式：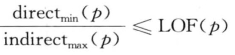

对任意o ∈ NMinPts（p） : reach-dist（p，o) ≥ directmin（p），由directmmin （p）的定义可知

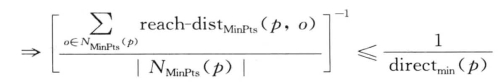
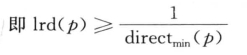
对任意q ∈ NMinPts （o） : reach-dist（o， q） ≤ indirectmax （p），由indirectmax （p）的定义可知

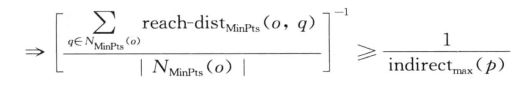
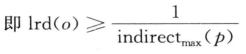
因此，可以得出

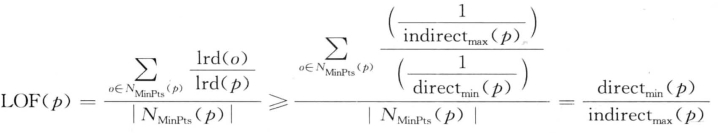
（b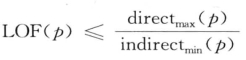）同理可证。

图6-10是定理6.1的一个例子，这里MinPts=3，dmin、dmax、imin、imax分别表示上面的directmin 、 directmax 、 indirectmin和indirectmax。

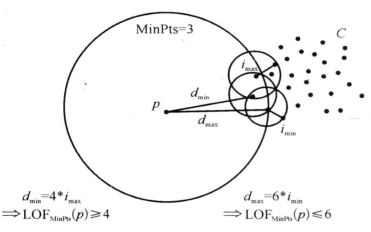
图6-10　定理6.1的图示

假设dmin= 4×imax ， dmax = 6×imin。根据定理6.1，有4≤LOF（p）≤6，即p的LOF在4和6之间。

4）边界的紧凑性

定理6.1给出了任意对象p的LOF值的上下界，但是这两个界是否具有紧凑性呢？即如果记LOFma为上界directmax /indirectmin，记LOFmin为下边界directmin /indirectmax，那么LOFmax和LOFmin之间的差距是多大呢？一个主要的结论是LOFmax和LOFmin的间距与direct/indirect的比值有关。在某些情况下，该间距比较小，另一些情形则会产生较大的间距。

给定directmin（ p）和indirectmax（p），用direct（p）表示它们的均值。类似的，indirect（p）表示indirectmin（ p）和indirectm（axp）的均值。用direct替代direct（p） 。

作如下假设： （directmax-directmin ） /direct = （indirectmax-indirectmin）/indirect

再另外引入一个变量pct， pct满足directmax= direct × （1 +pct%） ， directmmin = direct×（1—pct%）和indirectmax = indirect×（1 + pct %） ， indirectmin = indirect×（1—pct%）。那么可以得到如下结论：

即（LOFmax—LOFmin）/（direct/indirect）仅依赖于pct值，上面的关系可以用图6-11解释。如果把上式坐标看作是pct%为自变量的函数，不妨记为f（x）=4x/（1—x 2 ），那么f（x）的导数为：

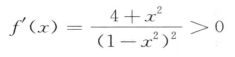
所以f（x）为x的单调递增函数，即等式左边根据pct的增加而增加。

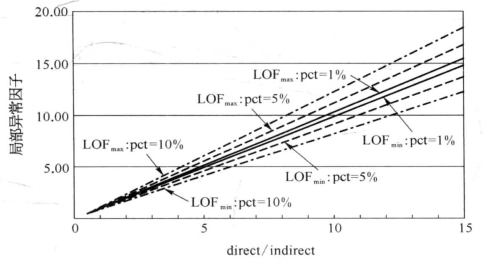
图6-11　LOF的上下界之差与direct/indirect依赖于pct

给出了上面的结论后，还留下这样一个问题：什么时候这些界就不再是紧凑的？下面的定理6.2给出了那些MinPts-邻域属于多个簇的对象p的局部异常因子的上下界，定理中首先对p的MinPts-邻域进行了划分。

定理6.2：令p是数据库中的一个对象，1 ≤ MinPts ≤| D |，且C1，C2， …，Cn是NMinPts （p）的一个划分，即NMinPts（ p）=C1∪C2∪…∪Cn ∪｛p｝，其中Ci∩Cj=φ， Ci≠φ1≤i， j≤n， i≠j。令ξi = | Ci | / | NMinPts（ p） |，表示Ci中的点在N MinPts（ p）中的百分比。符号的定义分别类似于directmin（ p） ， directmax（p），indirectmin（p）和indirectmax（ p），只是需要限制在簇Ci中。则下面不等式成立：

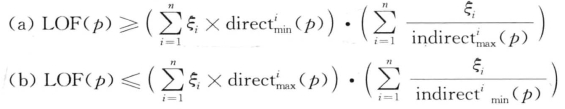
证明：这里证明第一个不等式，第二个同理可得。

由（p）的定义可得：

则有：

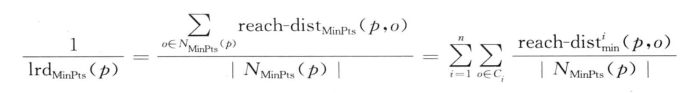
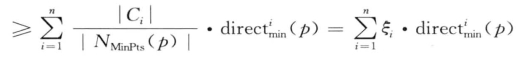
又由（p）的定义可得：

则有：

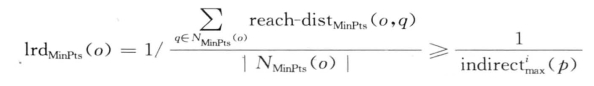
所以，

第二个不等式同理可证。

图6-12解释了定理6.2，这里MinPts =6，对象p的6-最近邻中有3个对象来自簇C1，其余3个来自簇C2。根据定理6.2， LOFmin =（0.5×d1min +0.5×d2min ）/（0.5/i1max+0.5/i2max），d1min和d2min分别表示p到C1和C2中6个对象的最小可达距离；i1max和i2max则表示q和q的6-最近邻之间的最大可达距离，q是p到簇C1和C2各自的6-邻域。出于简化目的，图6-5中没有给出的示例。

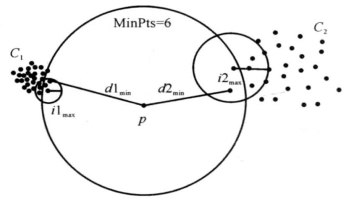
图6-12　定理6.2的图示

5）参数MINPTS的影响

前面分析了LOF的特性。对于在一个簇内部深处的对象，其LOF接近于1；对于其他对象，确定了LOF的上下边界，这取决于MinPts-邻域是否来自多个分簇。这些结论都是基于一个已经给定的MinPts值，下面讨论不同的MinPts对于LOF值的影响，并且讨论在计算LOF过程中如何选择合适的MinPts。

试验结果表明，当MinPts变化时，LOF值并不随之线性变化。为MinPts定义一个变化区间，用MinPtsLB和MinPtsUB分别表示这个区间的上下边界。

首先考虑MinPtsLB。一般，当MinPtsLB取值大于10时，能够有效地去除那些无用的距离变化值。此外，需要考虑对象p和簇C中多个对象之间的关系。如果C中对象的数目少于MinPtsLB，则C中每一个对象的MinPts-邻域会包含对象p，反之亦然。根据定理6.1，p和C中所有对象的LOF值都非常接近，这使得区分p与这些对象变得非常困难。另一方面，如果C中对象的数目多于MinPtsLB，则在C的内部深处对象的MinPts-最近邻居将不会包含p，但是CC的某些对象却被包含在p的邻居中。因此，依赖于p到C的距离和C自身的密度，对象p的LOF值可能不同于C中对象。一般而言MinPtsLB被认为是一个簇（如C）必须包含对象的最小数目，这时的MinPtsLB使得其他对象（如p）相对于这个簇成为局部异常点。这个MinPtsLB的取值可能依赖于应用，对于大多数情况，MinPtsLB取值在10到20之间比较好。

接下来考虑上界MinPtsUB。令C为一个由“近邻”对象组成的簇，则MinPtsUB会被认为是C中潜在的局部异常点对象的最大基数。“近邻”的含义是，directmin 、 directmax ，indirectmin和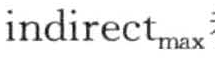都非常接近。此时，如果MinPts值超过了MinPtsUB，则定理1会使得C中所有对象的LOF都接近于1。因此，MinPtsUB应该选择“近邻”对象的最大数目，这些对象可能是局部异常点。

确定了MinPtsLB和MinPtsUB，可以在这个区间中计算每一个对象的LOF值。根据一个特定区间中LOF的最大值，可以用启发式的过程排列所有对象。也就是说，对象p的排列基于：max｛ LOFMinPts（p） | MinPtsLB≤MinPts≤MinPtsUB｝。

对该区间中所有对象的LOF值排列后，就可以确定有明显异常特征的对象，也可以采用其他的聚集函数如最小值、均值，而不仅仅局限于求最大值。例如利用均值能够平滑对象的异常特征。

6）局部异常因子（LOF）的计算

前面给出了局部异常因子的定义和性质，下面介绍LOF的计算。最简单但时间代价较高的办法是：

第一步：先产生所有点的MinPts-邻域（同时得到MinPts-距离），并计算到其中每个点的距离，并把计算的结果存入一个物化的数据库M中。

根据数据维数不同，可以采用不同策略：对低维数据，可以利用基于网格的方法来作kNN查询，整个计算时间为O（n）；对中维或中高维数据，必须采用索引结构如X-树、TV -树等，使得作kNN查询的时间为O（logn ），整个计算时间为O（nlogn）；对特高维数据，索引结构不再有效，时间复杂度提高到O（n2）。

第二步：利用物化的数据库M，计算每个点的局部异常因子。在该步计算中，需要扫描数据库两次，第一遍扫描，计算每个点的局部可达密度。第二遍计算出每个点的局部异常因子。该步的时间复杂度为O（n）。