基于距离的异常分析算法优化方案

1） DB （pct ， d）-异常［2］

定义6.3（DB（pct， d）-异常）：如果数据集D中一个对象p满足下列性质：数据集D中至少有pct%的对象与p的距离大于距离d，即集合｛q ∈ D | d（p， q） ≤ d｝的基数（集合中点或对象的个数）小于或等于D的大小的（1—pct%），则对象p称为相对于pct和d的异常，简称DB（pct， d）-异常。

其中d（p， q）表示p与q间的距离函数。

算法符号说明：设n是数据集D中的对象的数目，每个对象具有相同的k个属性（即数据维数为k）。 M是一个异常点的d-邻域内对象的最大数目，即M= n（1—pct%）。

本节介绍三种基于距离的DB（pct， d）-异常分析算法：基于索引的算法、嵌套-循环的算法和基于单元的算法。

（1）基于索引的算法（index-based）。算法采用多维索引结构（如R树或k-d树），检查每个对象O在半径d范围内的邻居。当对象O的M+1个邻居在d-邻域被发现，则停止搜索，O被确定为非异常点；否则，O是异常点。

这个算法在最坏情况下的复杂度为O（k×n2） （其中，k是维数，n是数据集合中对象的数目）。当k增加时，基于索引的算法具有良好的扩展性。但是，复杂度估算分析只考虑了搜索时间，而构造索引的任务本身是计算密集的，在一定程度上限制了基于索引的算法的应用。

（2）嵌套-循环（nested-loop）算法。嵌套-循环算法（图6-1）将内存的缓冲空间分为两半，数据集合分为若干个逻辑块，通过选择逻辑块装入每个缓冲区域的顺序，来改善I/O的效率。

算法将数据集读入缓冲空间，然后计算每对对象之间的距离，对每一个第一块缓冲区中的对象t，计算t的d-邻域对象个数count，直到count值超过M，则停止。算法的详细过程如下：

图6-1　嵌套-循环算法

算法举例：假设数据集四个逻辑块记为A、 B、C、D，每块含有数据集的1/4。根据算法按照以下顺序装入缓冲区间并进行比较：

①A与A，然后与B、C、D，该过程需读入4块数据。

② D与D（D不需再读入），然后与A（不需再读入）、B、 C，该过程需读入2块数据。

③ C与C，然后与D、 A、 B，该过程需读入2块数据。

④B与B，然后与C、 A、 D，该过程需读入2块数据。

因此该例中总共需读入10块数据，即需扫描数据集10/4=2.5遍。

嵌套-循环算法和基于索引的算法有相同的计算复杂度O（kn2 ），但它避免了索引结构的构建，并试图最小化I/O的次数。

（3）基于单元（cell-based）的方法。基于单元的算法不是逐个对象地对异常点计数，而是逐个单元地进行计数。

基本思想是把数据空间划分为边长等于的单元，每个单元有两个包围层，第一层的厚度是一个单元，第二层的厚度是［其中d是相对于DB（pct， d）-异常定义中的距离d］。

对一个给定的单元，累计三个计数：单元中对象的数目，单元和第一层中对象的数目（cell_+_1_layer_count），以及单元和两个层次中的对象的数目（cel l_+_2_layer_count ）。

然后按照以下方式确定异常点：

①当cell_+_1_layer_count≤ M时，在当前单元中的对象o被认为是异常点；否则，下一步的考察时，可以排除该单元中的所有对象，因为它们不可能是异常点。

②当cell_+_2_layer_count≤M时，单元中的所有对象都是异常点；否则，单元中的某些对象可能是异常点，为了探测这些异常点，对对象逐个进行处理。对单元中的每个对象o，检查它第二层中的对象，只有那些d-邻域内有不超过M个点的对象是异常点（一个对象的d-邻域由这个对象的单元、它第一层的全部和它第二层的部分组成）。

为简便起见，先以二维单元结构和整个数据库驻留内存为例详细介绍算法的设计思想和步骤，然后再推广到k维。

数据集中对象为二维情况下单元结构与性质（即k=2的情况）：

将数据空间划分为边长l等于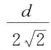的单元，行x和列y的交叉处单元记为Cx，y。Cx，y的第一层L1邻域是Cx，y的最近邻居单元，定义如下：

L1 （Cx， y） = ｛Cu，v | u=x±1， v=y±1， Cu，v≠Cx， y｝

除处于边界的单元外，一般每个单元都有8个L1邻域。

以下两个性质是发现异常点非常有用的规则：

性质6.1：在相同单元内的任何一对对象间的距离最大为

性质6.2：如果Cu，v是Cx，y的一个L1邻域，则任何一个对象P∈ Cu，v与任何一个对象Q∈ Cx，y之间的距离最大为d。

从性质6.1中发现，同一个单元中对角线长度最大，即；性质6.2则说明两个单元中的任意一对对象之间的距离不会超过单元对角线长度的2倍。Cx，y的第二层L2邻域是Cx，y的3个单元范围内的其他单元，即：

一般的，除处于或邻近边界的单元外，每个单元有72一32 =40个L2邻域。第一层L1的厚度是1个单元，第二层L2的厚度是2个单元。按照该方法选择的L2满足性质6.3：

性质6.3：如果Cu，v≠Cx，y既不是Cx，y的邻域L1也不是邻域L2，那么任何一个对象P∈Cu，v和任何一个对象Q∈Cx，y之间的距离一定大于d。

这是因为L1和L2的总厚度为3个单元，P和Q之间的距离必定超过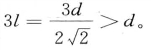

性质6.4：

（a）如果在Cx，y中对象个数超过M，则单元Cx，y中没有对象是异常点。

（b）如果在Cx，y∪L1（Cxx， y）中对象个数超过M，则单元Cx，y中没有对象是异常点。

（c）如果在Cx， y∪L1 （Cx， y）∪L2（Cx，y）中对象个数小于等于M，则单元Cx，y中的每个对象都是异常点。

数据集中对象具有二维属性，且完全驻留内存的数据集中检测DB（pct，d）-异常的具体算法FindAllOutsM如图6-2所示：

图6-2　FindAllOutsM算法

步骤2）将每个对象量化到它们相应的单元中；根据性质6.4（a），步骤3）将包含元组个数大于M的所有单元标记为red；由性质6.4（b），步骤4）将red单元的L1邻域单元标记为pink，因为它们不包含异常点；步骤5） b，将其他满足性质6.4（b）的单元也标记为pink 。最后步骤5） cii，标识满足性质6.4（c）的单元。

性质6.1～6.4有助于利用基于逐个单元的方法来识别异常点和非异常点，而不是基于逐个对象的方法。对于不满足上述性质6.4（a）～6.4（c）的单元，需要借助于逐个对象的方法，这些单元记为white单元（Cw）。步骤5） ciii，为判断在对象P∈Cw的d-邻域中有多少个位于Cw邻域L2单元中的对象Q，需要将对象P与Q进行比较。当d-邻域中的对象数量大于M时，P被认为是非异常点。在检查完所有的对象Q后，如果数量仍小于M，则P被认为是异常点。

二维情况下的复杂度分析：步骤1）时间复杂度O（m），其中m是单元总数（mN）；步骤2）和步骤3）时间复杂度分别是O（N）和O（m）；因为出现在red单元中的对象最小数目是M+ 1，因此步骤4）时间复杂度为O［N/（M+1）］；步骤5），在最坏情况下，即前面的步骤中没有单元被标记为red或pink，且每个单元都要执行步骤5）c，如果没有单元被标记，那么每个单元最多包含M个对象，因此步骤5）c中，单元中的40L2邻域的每个对象都要求检查M个对象，复杂度是O（40M2 ），因此步骤5）的时间复杂度是O（mM2）。

根据定义M= N（1—p），步骤5）的时间复杂度即O［mN2（1—p）2］，实际上，p是非常接近1的数，尤其是对于大数据集，因此复杂度可约估计为O（m），因此二维情况下算法FindAllOutsM的复杂度是O（m+N）。

上面的算法思想和算法都是针对二维情况，下面把它一般化到更高维的情况，即维数k由2到k＞2的情况，算法FindAllOutsM要求变化到k维单元结构，即数据空间需被划分为边长等于的单元以保证性质6.1和性质6.2。每个单元有两个层围绕它。第一层的厚度是一个单元。此时层1的定义如下：

为保证性质6.3，L2邻域的定义也被修改以概化到高维。由于，设层2厚度为x，则层1和层2厚度之后是x+1。为保证性质6.3，即要求（x+1）l＞d，因此选择x为个单元。即第二层的厚度是个单元。 （Cx1， …，xk）的邻域L2定义为：

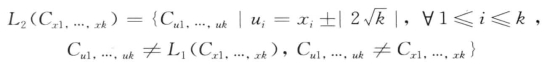
根据上面的定义保证了高维情况下单元满足上述4个性质。

高维情况下算法的思想和步骤同k = 2时。这里不再赘述。高维情况下复杂度分析：步骤1）～4）在k＞2的情况下是相同的，步骤5）的复杂度是约等于O（ck），其中c是依赖于单元数目的常数，k是维数。因此算法的复杂度是O（ck+N），另外，这里介绍的基于单元的算法是简化了的基于数据集驻留内存的算法，关于处理基于数据集驻留磁盘的扩展算法版本，有兴趣的读者请参见相关文献。

在基于DB（pct， d）-异常的算法中，基于单元区域的算法复杂度2与n呈线性关系，而与k呈指数关系。基于索引的算法和嵌套-循环的算法复杂度都是O（kN）。然而基于索引的算法由于建立索引的开销大，因此简单索引算法基本上没有竞争性；当k≤4时，基于单元区域的算法在N越大时优越性越明显。而当k≥5之后，嵌套-循环算法开始显现出优势。基于单元的算法，其复杂度与n线性相关，而与k指数相关［O（ck+n），其中c是依赖于单元数目的常数］。

基于距离的异常分析算法拓宽了多个标准分布的不一致检验的思想，避免了过多的计算。对于k维数据集的任何k都适用，不同于基于深度的方法，基于距离的异常分析算法不限定于较小的值k。但该方法要求用户设置参数pct和d，寻找这些参数的合适设置可能涉及多次的试探和错误。这种需要用户拥有相当的领域知识，并且进行人工干预算法的方法并不理想，下一小节介绍改进的基于距离的异常分析算法。

2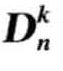） -异常分析算法［3］

上面介绍的方法中，输入参数pet与d很难确定，并且对于不同参数pct和d结果有很大的不稳定性，需要用户反复输入pct和d进行测试，以确定一个满意解。于是一种基于距离异常的新定义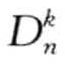被提出，下表为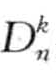异常检测算法中所用到的符号及其描述。

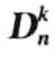异常检测算法中的符号及描述表(www.xing528.com)

用Dk（p）表示点p和它的第k个最近邻的距离，对某个点p根据它的Dk（p）进行排序，就得到下面的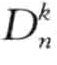异常的定义：

定义6.4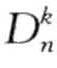（异常）：给定δ维空间中包含N个点的数据集，参数n和k（自然数），如果满足Dk（p′） ＞ Dk（p）的点p不超过n—1个，即|｛p′ ∈ D |Dk（p′）＞Dk（p）｝ ≤n—1，那么称p为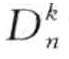异常。

如果根据数据点的Dk（p）距离，对数据点进行排序，在该排序中的前n个点则被认为是异常。这里两点间距离可以采用任意的Minkwinski距离Lp标准，如L1 （“manhattan”）或L2（ “Euclidean”）。在其他特定应用领域（如文本文档），也可以采用其他非标准度量距离函数，这样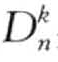异常定义更加通用。

该算法使用的一个关键技术是使用一个数据集的最小边界矩形MBR（ minimum bounding rectangle）来近似估计数据点。通过对每个MBR中的点p计算Dk（p）的上、下边界，可以判定是否包含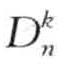异常，以及裁剪不可能包含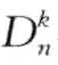异常的MBR。

下面将给出两个MBR之间的最小和最大距离的定义，用于计算MBR边界；给出点和MBR之间的最小和最大距离，用于辅助异常分析。

这里使用欧几里得距离的平方代替欧几里得距离作为距离度量标准，以降低计算代价。

dist（p， q）表示两数据点p和q之间的距离，［p1 ， p2 ， …， pδ］表示δ维空间中的数据点p，对角线上的两个端点：r=［r1， r2，…， rδ］和r′=［r1， r2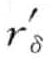，…， ］表示δ维矩形R（其中rii≤ 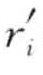，对任意1 ≤i ≤δ）， MINDIST（p， R）来表示点p和矩形R的最小距离，即R′中的每一个点与p的距离至少为MINDIST（p， R），如图6-3所示。

定义6.5：

用MAXDIST（p， R）表示点p到矩形R之间的最大距离，即R中的点与p的距离不超过超过MAXDIST（p， R）的距离，MAXDIST（p， R）可以计算如下：

定义6.6：

设R与S是两个MBR，其主对角线的端点分别是r、r′及s、s′，下面定义两个矩形R（r，r′）和S（s，s′）之间的最大和最小距离。

R与S之间的最小距离定义为MINDIST（R，S），R中的每个点至少在从S中任何一个点到MINDIST（R，S）的距离之内。

定义6.7：

两个MBR（R和S）间的最大距离：

定义6.8：

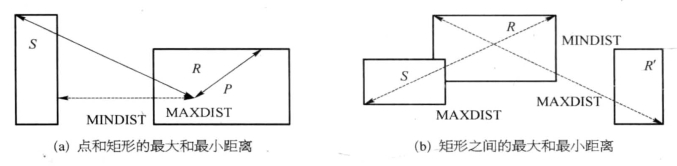
图6-3　点和矩形O以及矩形之间的距离

（1）嵌套-循环连接（nested-loop join）。循环嵌套算法的思想比较简单，对每个数据点p，计算它第k个最近邻的距离Dk（p），把具有极大Dk值的前n个点作为异常。在计算Dk（p）时，算法扫描整个数据库，可以先设置一个链表存放p的k个最近邻，然后对数据库中的每个点q计算dist（p， q），如果dist（p， q）小于p与链表中某个最近邻的距离，那么就把p放入链表（如果链表中的数据点超过k个，则把与p距离最远的那个点删除）。

算法每次处理一个点p需要扫描数据库N次（N为数据点数）。可以在对数据库进行一遍扫描时同时处理p1，…， pm点，同时计算它们的Dk（p）值以降低I/O负载，每次从磁盘读入点q时，可以同时对p1，…，pm作上面的检测，此时只需扫描数据库N/m次。

（2）基于索引连接（index-based Join）。即使利用I/O优化，循环嵌套方法的计算代价仍是昂贵的，特别是在数据点的维数较大时尤其如此。通过使用空间索引如R*-树可使距离计算工作量大大减少。

通过一些修剪简化减少计算点之间的距离：假设已经从整个数据集的一个子集中计算了点p的Dk（p），这个值显然是p真正的Dk（p）的上界，如果R*-树上一个点的MBR和p的距离超过当前的Dk（p），那么以这个点为根节点的子树里所有的点不可能是p的k最近邻。这个过程修剪了所有包含与p的k最近邻无关的点的子树。

另外，根据定义只计算前n个异常，还可以利用以下的修剪规则来优化计算Dk（p）。假设在基于索引算法中的每一步，都保存已计算好的前n个异常（暂时的），记为这些异常的Dk值的最小值。如果在计算某个点p的Dk（p）值时，发现Dk（ p）小于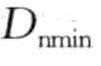，则可以判定p不是异常，这是因为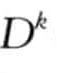（p）是随着检查的点数的增加而递减的，因此p不可能是前n个异常。在下面的nested-loop算法中将应用到该优化过程。

图6-4是用于计算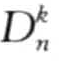异常的算法computOutliersIndex。该算法调用过程getKthNeighborDist（图6-5）作为子过程。

算法computOutliersIndex中第一步和第二步，首先将点插入到R*-树索引中（除R*-树外，其他索引结构也可使用）。R*-树用于计算每个点的k最近邻。此外，堆outHeap用于保存具有最大Dk值的n个点，并以升序排列以保证具有最小Dk值的点在堆的顶部，然后将具有最小Dk值的点（即堆顶部的点）保存到变量minDkDist中，作为getKthNeighborDist子过程的参数。算法中将outHeap初始化为空，minDkDist置0。

图6-4　computOutliersIndex算法

图6-5　getKthNeighborDist过程

第6至14步的循环调用getKthNeighborDist子过程。如果输入点的Dk值在前n个值中，将该点插入out Heap中。如果堆的大小超过n，则删除具有最小Dk值的点，并且更新minDkDi st值。

过程getKthNeighborDist建立链表结构nodeList（初始时为R*-树的根节点root）用于计算R*-树中的点p的Dk（p）。链表nodeList中的节点以到p的MINDIST的升序存储。每次迭代（5～24步循环）中，检查节点链表中的首节点。

如果节点为叶节点，算法处理叶节点中的对象点的过程时，借助堆nearHeap存储在被检查点中p的k最近邻点，并以降序排列。p.DkDist存储p到被检查点的Dk值（当k个点都被检查，p.DkDist值为∞）。第9～10步，如果任意一点q到p的距离小于p.DkDist，则将q插入nearHeap中。如果nearHeap中点的个数大于k，则删除nearHeap顶端的首节点，更新p.DkDist。如果p.Dkdist值小于minDkDist，则p不是异常点。因此，过程getKthNeighborDist第13步终止p的Dk值计算，并且返回。通过这种方法，getKthNeighborDist避免了不必要的非候选异常点的计算。

另一方面，如果在nodeList链表的首节点是内部节点，则将该节点的子节点添加到nodeList中。第18～19步，根据MINDIST值对nodeList排序。最后的21～23步，删除与p的距离超过p.DkDist的节点。包含在这些节点中的对象点显然是不在p的k最近邻中，可以被忽略。

（3）基于划分（Partition-Based）的算法。上述两种算法的缺陷是计算代价高，因为必须对每个点p来计算Dk（p），但异常检测的主要目标是找到前n个异常，而一般这个n值是比较小的，所以应该尽量避免计算其他那些点的Dk（p）。

基于划分的算法的基本思想是：如果某个点的Dk（ p）比较小的话，那么不可能是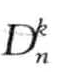异常。算法先对原始数据集进行划分，然后估计每个划分的Dk（p）的上、下界，如果能判定某个划分不可能包含异常，则可以直接把其删除；然后再从剩下的划分（候选划分）来计算异常。

下面是基于划分算法的基本步骤：

①利用聚类算法划分数据集。

②计算每个划分上、下界。

③判定候选划分是否包含异常。

④从候选划分的点中计算异常。

这里的第一步是划分数据集，将数据空间划分为单元（cell）然后将每个单元作为一个划分对于高维空间是不实际的，因为随着维数增加，单元的数量呈指数增长，对于4维以上的空间该方法效率很低。为使得相对较近的数据点分配在单独的划分中，采用聚类算法对数据集进行划分，每一个簇作为单独的一个划分。现有的许多聚类算法可以用来划分数据集，如BIRCH。然后用数据点的最小边界矩形来表示该划分，且最小边界矩形可能互相重叠。

需要注意的是，这里使用的聚类算法目的是为了高效地获得期望划分的启发式算法，而并不是用于计算异常。已经知道大多数聚类算法（包括BIRCH）也能执行异常检测，然而用聚类算法进行异常检测的异常并不精确，而更多的是在聚类过程中认为需要标识出来的孤立点。

第二步计算每个划分P中点的Dk值的上、下界。为了识别候选划分，需要计算划分P的Dk上下界P.lower和P.upper，满足下列性质：对P中的每个点p∈P，P.lower ≤Dk（p）≤P.upper。划分P的上下界P.lower/P.upper的计算可通过查找具有MINDIST/MAXDIST的划分P的最近的l个划分P1，…，Pl，且l个划分中的点的数目至少是k。

具体的算法如下：过程computeLowerUpper用于计算划分P的P.lower和P.upper（图6-6）。输入参数是包含所有划分的索引结构的根节点和minDkDist。该过程被计算候选划分的computCandidatePartit ions（图6-7）调用。过程computCandidatePartitions的思想是如果划分P的P.upper小于minDkDist（ 异常点Dk的下界），则该划分不包含异常，对该划分P的边界计算可以立即停止。

图6-6　计算划分的Lower、UpperBounds

图6-7　在划分集合PSet中计算候选划分的过程

过程computeLowerUpper与基于索引算法中的得到k-最近邻的过程getKthNeighborDist类似。把划分存储在两个堆lowerHeap和upperHeap中，分别以与P的MINDIST和MAXDIST的距离递减顺序存储，即MINDIST和MAXDIST值大的在堆的上面。

第三步是基于划分的算法中最重要的一步，确定可能包含异常的候选划分，把其余的划分删除。首先利用前一步计算的解来估计minDkDist异常的Dk值的下界，如果划分P满足P.upper≥minDkDist， P就成为候选划分。下界minDkDist使用划分的P.lower值用以下方法计算：假设P1，…，P1为P.lower最大的几个划分，并且至少包含n个数据点，那么minDkDist=min｛Pi.lower： 1≤i≤l｝为异常的Dk的下界。

图6-7给出了在划分集合PSet中计算候选划分的过程。这些分区存放在主存索引中，调用过程computeLowerUpper计算每个分区的上下界。但是，该过程并不是在计算所有分区的上下界后计算minDkDist值，而是计算在堆part Heap中存储的具有最大P.lower且包含至少n个对象点的分区。这些分区是以P.lower值的升序存储在partHeap堆中的，因此minDkDist即为part Heap堆中的顶端P.lower值。然后将minDkDist值作为参数传递给子过程computeLowerUpper（如图6-7第6步），这样，当分区P的P.upper值小于minDkDist时，即可提前停止P边界的计算。如果分区P的P.lower值比当前minDkDist值大时，将P插入堆part Heap中，并更新相应的minDkDist值（第8～13步）。

在循环的第17～22步，计算候选分区集合candSet。对于每个候选分区P，可能包含分区P中某个对象点的k个最近邻的分区Q插入到P.neighbors中（注意P.neighbors包含P）。

最后一步从候选划分中计算异常，如果划分中的所有数据点和它们的邻域能放入主存，那么可以把所有点装入主存空间索引。然后利用前面的基于索引的算法来计算异常。

但是当上面的条件不成立时，必须批处理来处理候选划分。在每一个批处理任务中，选取可以放入主存的一些划分和它们的邻域来处理。

最后的过程就是利用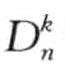异常定义得到最后的结果—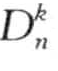—异常。