基于神经网络的分类算法：后向传播算法BP算法优化

前馈神经网络是神经元（单元）以层次方式排列而成的神经网络，每层由多个节点（神经元）组成，同层之间的节点（神经元）互不相连，相邻两层的节点（神经元）之间两两相连，前一层节点（神经元）的输出即为后一层节点（神经元）的输入。这种网络最初被称为多层感知器网络，之后，研究者提出了在这种网络上修改权值的BP算法（后向传播，back propagation）。 BP算法成为前馈神经网络学习算法中最常用的一种算法。

BP神经网络模型的特点是：各层神经元仅与相邻层神经元之间有连接；各层内神经元之间无任何连接；各层神经元之间无反馈连接。

后向传播学习算法的基本思想是，通过不断处理训练样本集，并计算输出层的结果及其与期望结果（每个样本已知类别）之间的误差，对于每个训练样本，不断修改权重以使网络输出与实际类别之间的均方差最小。将该误差向输入层逐层逆向传播给各节点，依次计算出各连接节点的参考误差，并据此调节各连接权值，使网络适应输出端误差到连接权值的映射。

具体步骤如下：

（1）初始化权：将可调参数（网络的权和阈值）初始化为较小的随机数（例如，由—1.0到1.0，或由—0.5到0.5）。

（2）对每个输入样本X作如下计算：

①向前传播输入：计算隐藏层和输出层每个单元j的净输入和输出。

首先，训练样本提供给网络的输入层。对于输入层的单元j的输出Oj等于它的输入Ij，即Oj=Ij。然后根据单元的输入是连接它的前一层单元的输出，隐藏层和输出层的每个单元的净输入用其输入的线性组合计算。

对给定隐藏层或输出层单元j，到单元j的净输入Ij是连接该单元的每个输入乘以其对应的权，然后求和，即

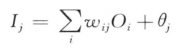
其中，wij是由上一层的单元i到单元j的连接权重；Oi是上一层的单元i的输出；而θj是单元j的偏差值。偏差值作为一个阈值，用来控制相应单元的活动程度。

隐藏层和输出层的每个单元接受一个净输入，然后利用一个激活函数对它进行运算。

给定单元j，它的净输入为Ij，则单元j的输出Oj用下式计算：

②计算后向传播误差：通过更新权和偏置以反映网络预测的误差，向后传播误差。

对于输出层单元j，误差Errj用式5-19计算：

其中，Oj是单元j的实际输出，而Tj是j基于给定训练样本的已知类标号的真正输出，Oj（1—Oj）是logistic函数的导数。

为计算隐藏层单元j的误差，考虑下一层中连接j的单元的误差加权和，隐藏层单元j的误差是Errj=Oj（1—Oj）∑kErrk ×wkj

其中，wkj是由下一较高层中单元k到单元j的连接权，而Errk是单元k的误差。

③权值修正。权值修正目的是反映传播的误差，修正按如下公式：

Δwij = （l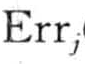Oi

wij = 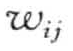+ Δ wij

其中，Δwij是权wij的变化，l是学习率，取值范围通常在0和1之间，一个经验规则是间学习率设置为1/t（t是已经对训练样本集迭代的次数）。

偏置由下式更新：

Δθj=（l） Errj

θj=θj +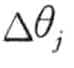

权值修正可以是每处理一个样本就更新，也可以是在处理完训练集中的所有样本之后再修正，通常前者产生的结果更准确，在实践中也应用更常用。

（3）判断误差是否收敛到所要求的精度，若满足，则结束，否则输入下一轮样本，转向（2）继续学习。

后向传播具体算法如图5-14所示：

图5-14　后向传播算法

说明：算法停止条件可以是：在批处理方式时，所获得的所有Δwij小于指定的阈值；被错误分类的样本占总样本数的比例小于指定的阈值；执行了指定次数的处理循环。

例5.8：一个多层前馈神经网络，通过后向传播算法学习的样本计算。设学习率为0.9。表5-8给出网络的初始权值和偏置值以及第一个训练样本X=｛1， 0， 1｝（类标号为1）。

表5-8　一个多层前馈神经网络例以及示例网络的初始权值和偏差

首先将样本提供给网络，计算每个单元的净输入和输出（表5-9）：

单元4：纯输入I4 = （w14 × 1 + w24 × 0 + w34 × 1） +（—0.4） = （0.2—0.5） +（—0.4）=—0.7，输出O4 = 1/（1+e-0.7） = 0.322；

单元5：纯输入I5=—0.3+0+0.2+0.2 = 0.1，输出O4 = 1/（1+e-0.1） = 0.525；

单元6：纯输入I6 = （ —0.3×0.33）+（—0.2×0.52）+0.1=—0.105，输出O6 =1/（1+e0.105） =0.474

然后计算每个单元的误差，并后向传播（表5-10）。

单元6：误差Err6 = O6 × （1—O6）×（T6—O6） = 0.474 × （1—0.474）×（1—0.474） =0.1311

单元5：误差Err5 = O5×（1—O5） × ［（Err6×w56）］=0.525×（1—0.525）×［（0.1311×—0.2）］=—0.006 5

单元4：误差Err4 = O4×（1—O4） × ［（Err6×w46）］= 0.322 ×（1—0.322）×［（0.1311×—0.3）］=—0.008 7

表5-9　净输入和输出的计算表

表5-10　计算每个节点的误差

(www.xing528.com)

权和偏置的更新见表5-11。

Δw46 =l×Err6 ×O4 =0.9×0.1311×0.322=0.03799

w46 = w46+Δw46=—0.3 + 0.03799=—0.26201

同理求得w56 ，w14 ， …

Δθ6 = l×Err6 = 0.9×0.1311 = 0.11799

θ6 =θ6+Δθ6 =0.1+0.11799=0.21799

同理求得θ4，θ5。

表5-11　计算权和偏置的更新

神经网络的主要缺点是用加权链接单元的网络表示的知识很难被入理解。在经过神经网络构造和训练得到一个好的神经网络后，为将神经网络中隐藏的知识以一种易于理解的方式明确表达出来，一个重要的工作是从神经网络中抽取规则。

由神经网络提取规则的第一步通常是网络剪枝。通过剪去对训练网络影响最小的加权链简化网络结构，例如，如果删除一个加权链不导致网络的分类精确度下降，则应当删除该加权链。一旦训练网络已被剪枝，然后可以使用一些方法进行链、单元或激活值的聚类。例如，使用聚类发现给定训练的两层神经网络中每个隐藏单元的共同激活值集合（图5-15）。分析每个隐藏单元的这些激活值，导出涉及这些激活值与对应输出单元值组合的规则。类似地，研究输入值和激活值的集合，导出描述输入和隐藏单元层联系的规则。最后，两个规则的集合可以结合在一起，形成IF-THEN规则。其他算法可能导出其他形式的规则，包括M-of-N规则，具有M-of-N测试的判定树、模糊规则和有穷自动机等。

图5-15　隐藏单元的共同激活值集合

下面给出一个例子，作为规则提取算法过程的解释。

通过对每个隐藏层节点的激活值通过聚类做离散化，得到每个隐藏层节点的激活值（cluster activation values）集合：

即各隐藏层的节点数目分别是3，2，3，计算每个组合情况，得到18种输出，见表5-12。

表5-12　输出组合

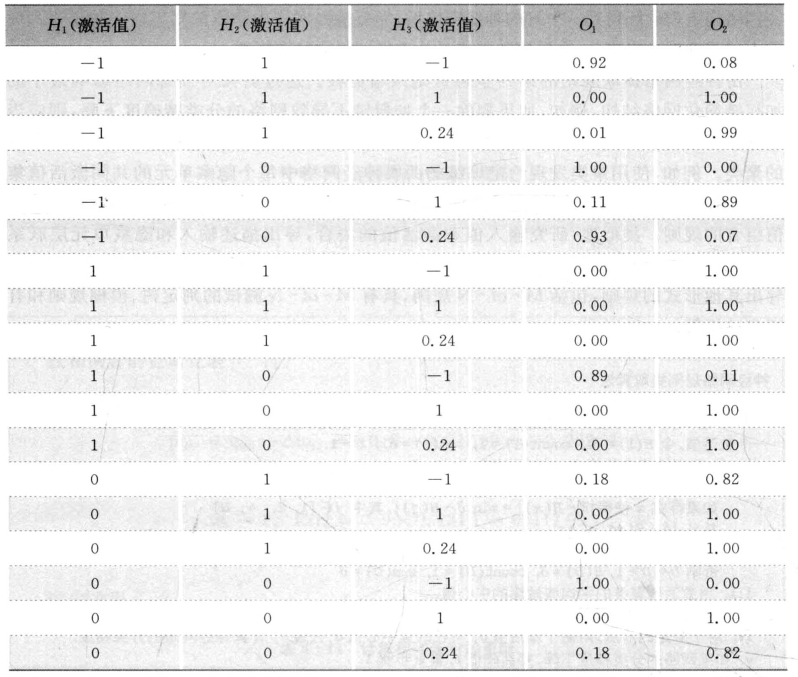
结合表5-12，可得到隐藏层到输出层的规则：

R11： H2 = 0 ， H3=—1C1=1，C2=0

R12 ： H1=—1， H2 = 1， H3=—1C1=1，C2=0

R13 ： H1=—1， H2 = 0， H3 =0.24C1 = 1， C2 = 0

其余情况C1= 0，C2=1

求输入层到隐藏层的规则：

从隐藏层到输出层的规则结果集看出，对于隐藏层节点1，只出现了激活值1，没有出现0和—1的情况，

R21 ： I5 = 1H1=—1

R22 ： I1 = I5 = I6 = 0， I7 = 1H1=—1

对于隐藏层节点2，只出现了激活值0，1

R23： I2 = 1H2 = 1

R24： I7 = 1H2=1

R25 ： I2 = I7 = 0H2 = 0

对于隐藏层节点3，只出现了激活值—1，0.24，没有出现1

R26 ： I5 = 0H3=—1

R27： I4 = I6 = 1H3=—1

R28： I3 = I5 = 1， I7 = 0H3 = 0.24

R29 ： I4 = 0 ， I5 = I6 = 1H3= 0.24

由输入层到隐藏层的规则以及隐藏层到输出层的规则，可以求出神经网络对应的分类规则：

用R25 ，R26 ，R27代替R11有

I2 = I7 = 0 ， I5 = 0C1 = 1， C2 = 0

I2 = I7 = 0， I4 = I6 1C1 = 1， C2 = 0

用R21 ，R22 ，R23 ，R24 ，R26 ，R27代替R12有

I4 = I5 = I6=1C1=1，C2=0

I1 = I5 = I6 = 0， I7 = 1C1 = 1， C2 = 0

用R21 ，R22 ，R25 ，R28 ，R29代替R13有

I2 = I7 = 0 ， I3 = I5 = 1C1 = 1， C2 = 0

图5-16表示用IF-THEN-ELSE表示的神经网络提取的规则：

图5-16　由训练神经网络提取规则