基于决策树的分类算法：ID3与C4.5

前面一小节对决策树的基本原理和过程做了详细的介绍，这一小节介绍两种经典的决策树构造算法：ID3算法和C4.5算法。

给定一个训练样本集，每个样本具有相同的结构，由若干个成对的“属性-值”对构成。

例5.5：考察影响打高尔夫球的天气条件的记录，类别属性表示“是否适合运动”。非类别属性有：天气、温度、湿度及风况（表5-2）。

表5-2　打高尔夫球的天气条件属性

训练数据如下（表5-3）：

表5-3　打高尔夫球的天气条件训练数据

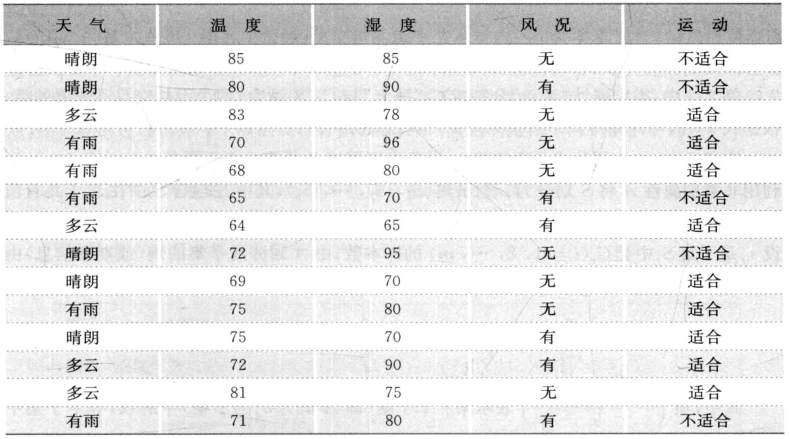
1） ID3算法

ID3算法的核心问题是选取在树的每个节点要测试的属性。所选的属性应该是最有助于分类数据的属性，ID3算法使用信息增益标准从候选属性中选择属性。

ID3算法基于信息论，下面给出一些信息论的相关概念：

定义5.6（自信息量）：根据人们的实践经验，一个事件给予人们信息量的多少，与这一事件发生的概率大小有关：一个小概率事件的发生，给予人们的信息量多；相反，一个大概率事件的出现，给予人们的信息量少。用I（A） =—log2p （p表示事件A发生的概率）来度量事件A给出的信息量，称为事件A的自信息量。

熵是信息论中广泛使用的一个度量标准，刻画了任意样本的纯度（purity），用于度量样本的均一性。

定义5.7（信息熵）：若一次试验有n个可能结果（事件），它们出现的概率分布P=（p1 ， p2 ， …， pn），用Entropy（P）信息熵度量一次试验所给出的平均信息量，计算公式为

例如，若P为（0.5，0.5），则Entropy（ P）等于1；若P为（0.67，0.33），则Entropy（P）为0.92；若P为（1，0），则Entropy（P）为0。

定义5.8（给定的样本分类所需的期望信息）：设S是s个数据样本的集合，假定类别属性具有m个不同值，定义m个不同类Ci（i = 1，2，…，m）， si是类Ci中的样本数（即|Ci| ），pi是任意样本属于Ci的概率，并用si/s估计，对一个给定的样本分类所需的期望信息由式5-6给出：

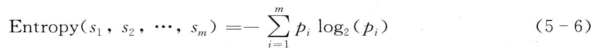
例5.5中，类别属性“运动”分割成C1“适合”与C2“不适合”两个不相交且不遗漏的类，根据式5-2，可计算得：Entropy（s1，s2） = Entropy（9/14，5/14） = 0.94。

定义5.9（由A划分成子集的熵）：设非类别属性A具有v个不同值｛a1， a2，…， av｝，利用非类别属性A将S划分为v个子集｛S1， S2， …，Sv｝；其中Sj包含S中在A上具有值aj的样本。若A选作测试属性，则这些子集对应于由包含集合S的节点生长出来的分支。设sij是子集Sj中类Ci（i=1，2，…，m）的样本数，由A划分成子集的熵（或期望信息）由式5-7给出：

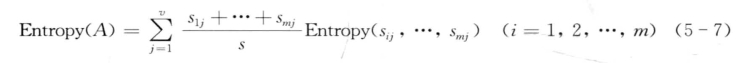
其中，项表示第j个子集（即A值为aj的子集）中的权，等于子集中的样本个数除以S中的样本总数。

对于给定的子集Si，

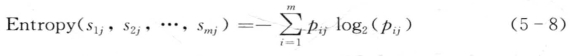
其中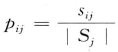，是Sj中的样本属于类Ci的概率。

例5.5中，对于属性“天气”有：

定义5.10（信息增益）：是指两个信息量之间的差值，其中一个信息量是识别一个S的元素所需信息量，另一个信息量是属性A的值已经得到以后识别一个S的元素所需信息量，即信息增益与属性A相关。信息增益定义为：

例5.5中，对于属性“天气”，有：

Gain（天气，S） = Entropy（s1 ， s2）—Entropy（天气）=0.94—0.694 = 0.246

如果改为考虑属性“风况”，计算Ent ropy（风况）值为0.892， Gain（风况，S） = Entropy（s1 ， s2）—Entropy（风况）=0.048，因此属性天气比属性风向提供了更高的信息收益，取得的信息量更大。

ID3的基本思想：构造决策树，决策树的每个节点对应一个非类别属性，每条边对应该属性的每个可能值。以信息熵的下降速度作为选取测试属性的标准，即所选的测试属性是从根到当前节点的路径上尚未被考虑的具有最高信息增益的属性。对于非终端的后继节点，用相同的过程选择一个新的属性分割训练样本，直到满足以下两个条件中的任一个：

（1）所有的属性已经被这条路径包括。

（2）与这节点关联的所有训练样本都具有相同的目标属性值。

ID3算法的代码如图5-6所示。

下面给出一个ID3算法的例子：

图5-6　用于建立决策树模型的ID3算法。

类别属性“运动”有两个不同值（即｛适合，不适合｝），得到两个不同的类（m=2）。设类C1对应于（适合），类C2对应于（不适合）。类C1有9个样本，类C2有5个样本。利用式5-2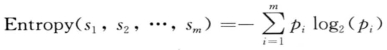：，计算对给定样本分类所需的期望信息：

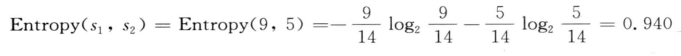
下一步计算每个属性的熵。从属性“天气”开始，观察“天气”的每个样本值的“适合”和“不适合”分布。对每个分布计算期望信息。

对于天气为“晴朗”： s11 = 2 s21 = 3 Entropy（s11 ， s21 ） = 0.971

对于天气为“多云”：s12 = 4 s22 = 0 Entropy（s12 ， s22） = 0

对于天气为“有雨”：s13 = 3 s23 = 2 Entropy（s13 ， s23） = 0.971

应用式计算得，

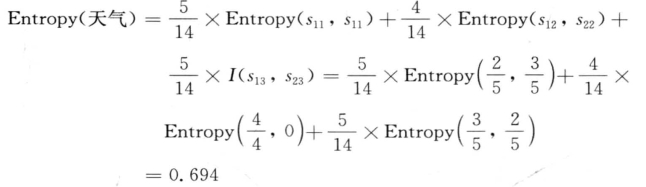
因此，这种划分的信息增益是(www.xing528.com)

Gain（天气，S） = Entropy（s1 ， s2）—Entropy（天气）= 0.94—0.694 = 0.246

类似的，Gain（风况，S） =0.048， Gain（温度）=0.029， Gain（湿度）=0.151。

得到如图5-7所示的决策树：

图5-7　例5.5的决策树

2） C4.5算法

ID3算法被限制为取离散值的属性：学习到的决策树要预测的目标属性必须是离散的；树的决策结点的属性也必须是离散的。C4.5算法对原始的ID3算法进行了扩充，它除了拥有ID3算法的功能外，还增加了：

①使用增益比率的概念。

②合并具有连续值的属性。

③处理缺少属性值的训练样本。

④通过使用不同的修剪技术以避免树的不平衡。

⑤ k次迭代交叉验证。

⑥规则的产生。

下面主要介绍以下三个部分：

（1）使用增益比率（gain ratio）。信息增益偏袒具有较多值的属性，太多的可能值必然把训练样本分割成非常小的空间，相对训练样本，将会有非常高的信息增益，特别地，当属性的每条记录的值都不一样，那么Entropy（A， S） =0，于是Gain（A， S）最大。例如，考虑属性‘日期’（Date），它有大量的可能值（如2004年11月10日），如果把该属性加到例5.5的表5-3中，则它在所有属性中将具有最大的信息增益，因为单独的Date属性就可以完全预测训练数据的目标属性，于是这个属性会被选作树的根结点的决策属性，生成一棵深度为1但却非常宽的树，这棵树可以理想地分类训练数据，但这个决策树对分析后来的数据性能将相当差，这样的决策树不是一个好的分类器。

为了避免这个不足的情况，选用其他度量而不是信息增益来选择决策属性。一个可选的度量标准是增益比率。增益比率通过加入分裂信息（split information）来惩罚类似Date的具有较多值的属性。

定义5.11（分裂信息）：分裂信息是数据样本集合S关于属性A的各值的熵，用于衡量属性分裂数据的广度和均匀性，由式5-10计算：

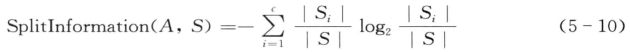
其中，S1到Sc是含有c个值的属性A分割S而形成的c个样本子集。

定义5.12（增益比率）：增益比率度量由信息增益和分裂信息度量共同定义，由式5-11计算：

分裂信息SplitInformation（A， S）是根据类别属性A的值分隔S的信息量，它阻碍选择值均匀分布的属性，例如，考虑一个含有n个样本的集合被属性A彻底分割，则分裂信息值为log2 n；一个布尔属性B分割同样的n个实例，如果恰好平分两半，那么分裂信息是1。如果属性A和B产生同样的信息增益，那么根据增益比率度量，显然属性B具有更高的增益比率。

在例5.5中，由式5-6计算得，SplitInformation（天气，S）为：

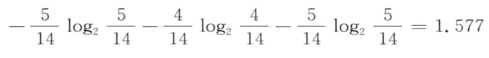
因此，属性天气的增益比率为0.246/1.577=0.156。

而SplitInfo（风况，S）为：

因此，属性风况的增益比率为0.048/0.985 = 0.049。

使用增益比率代替增益来选择属性时，产生的一个实际问题是，如果某个属性对于S的所有样本有几乎同样的值，使|Si|≈|S|，则分母分裂信息值可能为0或非常小，将导致增益比率无定义或增益比率非常大。为避免选择这种属性，可以采用一些启发式规则，比如先计算每个属性的增益，然后仅对增益高于平均值的属性应用增益比率测试。

（2）处理连续值属性。ID3算法最初的定义假设属性值是离散值，但在实际环境中，存在大量连续型属性，可以按下面的方法处理连续范围属性：

①把连续值属性的值域分割为离散的区间集合。例如，对于连续值的属性A，可创建一个新的基于阈值的布尔属性ABool，如果A＜c，那么ABool为真，否则为假。

但这里存在的问题是如何选取最佳阈值c，下面介绍一种最简单的合适阈值选取方法——候选阈值是相应的连续属性A值之间的中间值。

在表5-4中，对于连续值属性“温度”，候选的阈值可以是： （48+60）/2和（80+90）/2，然后计算候选属性（温度＞54）和（温度＞85）的信息增益，选择最好的，如（温度＞54）。

表5-4　阈值选取方法

③假设属性A有连续的属性值，考察训练集上这个属性的值，依照升序排列依次为v1， v2 ， … ， vm。对于每个值vj （j = 1， 2，…， m），将A的记录值划分为两部分：一部分落入在vj的范围内（小于或等于vj ），另一部分则大于vj。针对每个划分分别计算增益或增益率，然后选择出最大化增益的分块方式。

在例5.5中，对于湿度属性，通过考察每个划分的信息，发现最佳分割点是75，因此这个属性的划分定为｛≤75，＞75｝。

（3）处理缺少属性值的训练样本。在某些情况下，数据集中的数据还可能缺少某些属性的某些值。例如，在医学领域希望根据多项化验指标分析患者的结果，然而可能仅有部分患者具有验血结果，而部分患者缺少验血结果，这种情况下，经常需要根据此属性（验血结果）值已知的其他实例来估计缺少的属性值。

下面介绍处理缺少属性值的训练样本的几个策略：

假定＜x， C（x）＞是S中的一个训练样本，并且属性A的值A（x）未知。处理缺少属性值的一种策略是赋给它节点n的训练样本中该属性的最常见值，或赋给它节点n的被分裂为C（x）的训练样本中该属性最常见的值。

另一种复杂的策略是为属性A的每个可能值赋予一个概率，而不是简单地将最常见的值赋给A（x）。例如，给定一个布尔属性A，如果节点n包含6个已知A=1和4个A=0的样本，那么A（x）=1的概率是0.6， A（x） =0的概率是0.4。于是，实例x的60%被分配到A=1的分支，40%被分配另一个分支。这些片段样本（fractional examples）的目的是计算信息增益。另外，如果有第二个缺少值的属性必须被测试，这些样本可以在后继的树分支中进一步细分。

在例5.5中，设共有14个训练样本集，其中一个样本的天气属性有未知值。已知天气属性的其他13个样本分布如表5-5所示：

表5-5　训练样本集

未知值的样本概率在其属性值对应P（晴朗）为5/13，P（多云）为3/13，P（有雨）为5/13。沿着路径往下传递的样本数量为：天气=晴朗是5+5/13，天气=多云是3+3/13，天气=有雨是5+3/13，它的分类样本为5+5/13+3+3/13+5+5/13=14。

3）两种算法的评价

ID3算法是经典的决策树分类算法，C4.5对ID3进行了一定程度的扩展，增加了对连续性属性的支持，降低了对训练样本数据质量的要求。但两者的局限性也是明显的，ID3和C4.5算法中，由于每个离散型属性必须分成多叉树，每个子节点表示一个属性值，这使得属性被过度细分，不能表现出精确的分类结果；此外，C4.5算法对于连续属性值简单地一分为二的处理方式，也显得不够细致，例如，如果连续属性在某几个区间呈现出聚集特性，C4.5算法无法精确识别。同时，ID3/C4.5不具备良好的可伸缩性，当数据量较小时，他们是很有效的，但是当算法用于处理大规模训练集（例如上百万条样本数据）时，决策树的构造过程将会慢得无法忍受，算法的有效性和可伸缩性成为瓶颈。