基于神经网络的优化技术

神经网络是分类分析中的重要技术之一，基于神经网络的分类方法可以通过提供的训练样本及样本所属的类别对神经网络的权值进行调整，从而使该神经网络具有能够预测输入样本的正确类标号以进行分类的能力。

神经网络是一组连接的输入/输出单元，其中每个连接都与一个权相连。

在神经网络中，前馈神经网络是一个重要的组成部分。图5-4展示了一个简单的三层神经网络，它是一个多层前馈（multilayer feed-forward）神经网络，包含输入层（input layer）、隐藏层（hidden layer）和输出层（output layer），层之间的连接线表示这三层通过可修改的权相连接。输入对应于对每个训练样本度量的属性，提供给输入层的单元；这些单元的加权输出依次提供给称为隐藏层的单元（第二层）；该隐藏层加权输出输入到另一隐藏层；如此下去；隐藏层的数量是任意的，最后一个隐藏层的加权输出作为构成输出层的单元的输入。输出层发布给定样本的网络预测。隐藏层和输出层的单元，可称为输出单元。图5-4中所示的多层神经网络具有两层输出单元，称为两层神经网络；包含两个隐藏层的网络称为三层神经网络，等等。该图中因为权都不回送到输入单元或前一层的输出单元，称此网络是前馈的。若每个单元都向下一层的每个单元提供输入，则称网络是全连接的。

图5-4　一个简单的三层神经网络

神经网络模型主要由三方面的要素决定：一是神经元的计算特性；二是网络的拓扑结构；三是连接权值的学习规则。

1）神经元模型

神经元是神经网络的基本计算单元，是用人工方法模拟生物神经元而形成的模型，是对生物神经元的模拟与简化。它一般是多输入、单输出的非线性单元（如图5-5是一个完整的神经元结构）。

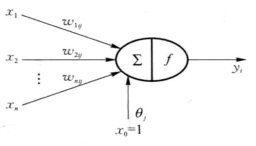
图5-5　神经元模型

神经元模型可以描述为：

其中，xj（j=1， 2，…， n）为输入信号（从其他神经元传来的输入信号）， θj是该神经元的阈值，wij表示从神经元i到神经元j的连接权值。

神经元的输出是各个输入的加权和的函数f（xi），这一函数被称为神经元的激活函数（activation function）。激活函数用符号表现单元代表的神经元的激活功能，将一个较大的输入值域到较小的区间0和1。常用的三种非线性激活函数有中心限幅、阶跃函数和Sigmoid函数等。

如：f（x）为阶跃函数，则(www.xing528.com)

S型函数，通常是在（0，1）或（—1，1）内连续取值的单调可微分函数，常用指数等一类曲线表示：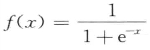

2）神经网络拓扑

神经网络是由大量的神经元连接而成的网络，神经网络拓扑结构形式多样，主要可以分为以下几类：

（1）前向神经网络。神经元分层排列，各个神经元只接受前一层的输入，并输出到下一层，没有反馈，如图5-4所示。

（2）反馈神经网络。神经元具有广泛的反馈连接，系统通过一个动态过程达到希望的状态。

（3）自组织网络。神经元按照某种次序排列，通过相邻神经元的互相作用完成一定的功能，也称为竞争神经网络。

在开始训练神经网络之前，需要确定网络拓扑，必须处理以下几个主要问题：

（1）输入层单元数（属性个数）：类似于决定某个属性为分支属性问题。

（2）隐藏层个数：最简单情况下，常常只有一个隐藏层。

（3）隐藏层单元数：使用神经网络算法时，隐藏层的最佳单元数的选择是非常困难的，也没有明确的规则。如果隐藏层单元个数太少，可能无法学习目标函数；如果隐藏层单元个数太多，可能出现过适应问题。神经网络的结构设计是一个不断试错的过程。

（4）输出层单元数：与类别个数有关。

（5）权的初值选择：将影响结果的准确性。一旦网络经过训练，并且其准确率不能被接受，则通常用不同的网络拓扑或使用不同的初始权值，重复训练过程。

（6）训练样本中每个属性值的处理：对训练样本中每个属性值进行规范化有助于加快学习过程。通常，将输入值规范化，使得其值落入0.0和1.0之间。离散值属性可以重新编码，使得每个域值对应一个输入单元。例如，属性A的定义域为（a0， a1， a2），则可以分配三个输入单元表示A，即用I0、I1、I2作为输入单元。每个单元初始化为0。如果A=a0，则置I0为1；如果A=a1，则置I1为1；如此下去。一个输出单元可以用来表示两个类（值1代表一个类，值0代表一个类）。但如果类别多于两个时，则每个类使用一个输出单元。

3）网络权值

神经网络的连接权值的确定一般有两种方式：一是通过设计计算确定，即所谓的死记式学习；二是网络按一定的规则通过学习（训练）得到。大多数神经网络使用后一种方法确定其网络权值。