介绍k-means和k-medoids算法的划分方法

已经知道，给定一个包含n个样本的数据集，划分方法是将数据分为k个划分（k≤n），每个划分表示一个簇，同时满足：

①每个簇至少包含一个样本。

②每个样本必须属于且仅属于一个簇。

下面详细介绍两种最常用的启发式方法：k-平均（k-means）算法和k-中心点（k -medoids）算法。

1）基于质心的k-means聚类算法

k-means算法（图4-11）是基于质心的方法，即相似度计算是根据一个簇中对象的平均值（簇的质心）进行的，目标是找到数据的k个划分使得准则函数（见3.2.4）收敛（k -means算法中簇的数量k是在算法运行前确定的）。具体步骤如下：

①选择一个含有随机样本的k个簇的初始划分，计算这些簇的质心。

②根据欧氏距离把剩余的每个样本分配到距离它最近的簇质心的一个簇。

③计算被分配到每个簇的样本的平均值，作为新的簇的质心。

④重复步骤②和③，直到k个簇的质心点不再发生变化或准则函数收敛。

图4-11　k-means算法

例4.5：如图4-12所示，坐标表示5个点｛X1， X2， X3， X4， X5｝作为一个聚类分析的二维样本：X1=（0， 2）， X2=（0， 0），X3=（1.5， 0）， X4=（5， 0）， X5=（5， 2）。假设要求的簇的数量k=2，选用平方误差准则作为衡量聚类划分准则。

图4-12　聚类分析的5个二维样本

第1步，由样本的随机分布形成两个簇：

C1=｛X1， X2， X4｝和C2=｛X3， X5｝；

这两个簇的质心M1和M2是：

M1=｛（0+0+5）/3， （2+0+0）/3｝=｛1.66，0.66｝；

M2=｛（1.5+5）/2，（0+2）/2｝ =｛3.25，1.00｝ ；

样本初始随机分布之后，方差是：

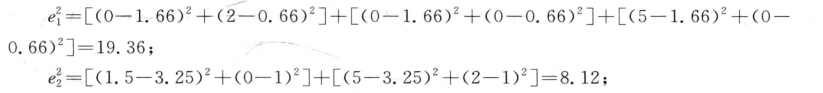
误差平方和是：

第2步，取距离其中一个质心（M1或M2）最小的距离分配所有样本，簇内样本的重新分布如下：

d（ M1 ， X1 ）=（1.662+1.342）1/2=2.14和d（ M2 ， X1 ） =3.40X1 ∈ C1 ；

d（M1， X2）=1.79和d（ M2 ， X2） = 3.40X2 ∈ C1

d（M1， X3）=0.83和d（M2， X3） =2.01X3 ∈- C1

d（M1， X4）=3.41和d（M2， X4）=2.01X4 ∈- C2

d（M1 ， X5）=3.60和d（M2， X5）=2.01X5∈C2

新簇C1=｛X1， X2， X3｝和C2=｛X4， X5｝

第3步，计算新的质心：

M1=｛0.5， 0.67｝； M2=｛5.0， 1.0｝。

相应的类内方差及误差平方和分别是：

可以看出第一次迭代后，误差平方和显著减小（从值27.48到6.17）。在这个简单的例子中，第一次迭代同时也是最后一次迭代，因为如果继续分析新中心和样本间的距离，样本将会全部分给同样的簇，不将重新分配，算法停止。

（1） k-means算法时间和空间复杂度。

①时间复杂度与数据集的大小是线性关系：O（nkl），其中n是样本数量，k是簇的数量，l是算法收敛时已迭代的次数（通常k和l预先给定）。

②空间复杂度是O（k+n）。

③算法不依赖样本顺序：给定一个初始簇分布，无论样本顺序如何，聚类结束后生成的簇都一样。

（2） k-means算法的局限性。

①在使用迭代的划分聚类算法时，缺少一个有关可应用于选择初始划分的最佳方向、更新分区、调整簇数和停止准则等方面的指导，因此，k-means算法要求用户必须事先给出要生成的簇的数目。

②由于k-means算法通过计算簇的平均值来使准则函数最小化，算法只有在簇的平均值被定义的情况下才能使用，这可能不适用于某些应用，如涉及有类别属性的数据。

（k-means算法对噪声和异常点非常敏感，因为即使是少数这样的数据对平均值的影响也相当大，因此算法必须在预处理时清除异常点，另外需要进行后处理，包括合并相互接近的簇、清除小的簇（因为它们可能表示异常点的集合）、分割可能导致错误的松散的簇。

（3） k-means算法的变体（k-modes， k-prototypes）。为克服k-means算法的局限性，提出了许多k-means算法的变体，这些变体的不同在于初始k均值的选择、相似度的计算和簇均值的计算策略等方面。

①初始点的选择不同聚类的结果也不相同（图4-13），因此，在初始点选取上有很多变体算法。(www.xing528.com)

图4-13　初始点的选择不同对聚类结果的不同

②基于误差准则在许多应用中不适用，如：大小很不相同的簇或具有凹状的簇。

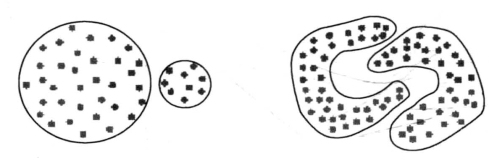
图4-14　误差准则不同处理不同形状的簇

③k-means被限定在欧氏空间中，但k-means的变体可被用于其他类型的数据。

k-means算法使用的限制条件常常是针对数值型数据。它的一个变体k-prototypes算法可以针对数值与离散两种混合类型的数据进行聚类，在k-prototypes算法中定义了一个对数值和离散两种属性都计算的相异度度量：sn+γsc（sn是在数值属性上由欧几里得距离的平方定义的相似度度量，sc是在离散属性上由两个样本之间离散数据的不匹配数量所定义的相似度度量，γ是一个避免两个属性失衡的权重）。

k-modes方法是k-prototypes算法的一个简化，用于对离散属性数据聚类的快速聚类算法，在保留了k-means算法效率的同时将k-means的应用范围扩大到离散数据，算法用簇的模替代k-means算法中的均值，采用基于频率的方法来修改簇的模，使用新的相异度度量处理样本，由于不存在sc，因此在k-modes算法中权重y不再需要。该算法的最大优点是对大数据集具有扩充性。

2）基于有代表性的对象的k-中心点（k-medoids）方法

针对k-means算法对孤立点敏感这一缺陷，提出了k-中心点方法。它不是采用簇中样本的平均值为簇的代表，而是选用簇中位置最中心的样本对象，即中心点（medoids）为簇的代表。因此，k-中心点方法对于噪声和异常点没有k-means方法敏感，且它与样本访问的顺序无关，而且不会随着数据点的平移和正交变换改变，适用于距离相似度且没有欧氏空间的限制。

k-medoids聚类算法的基本策略：不采用簇中样本的平均值作为参照点，选用簇中位置最中心的样本——中心点作为参照点。原则是基于最小化所有样本与其参照点之间的相似度之和。

k-medoids具体步骤：

①为每个簇随意选择一个代表样本Oj。

②根据剩余样本与代表样本的距离将剩余样本分配给最近的一个簇。

③反复地用非代表样本Orandom来替代代表样本，以改进聚类的质量。聚类结果的质量用代价函数来估算（代价函数是一个用来度量样本与其参照样本之间的平均相似度的度量函数）。

判定一个非代表样本Orandom是否是当前一个代表样本Oj的好的替代，考虑以下四种情况：

图4-15　非代表样本Orandom是否是当前一个代表样本Oj的好的替代四种情况

对于每一个非中心对象p，

第一种情况：p当前隶属于中心对象Oj。如果Oj被Orandom所代替作为中心点，且p离一个Oi最近，i≠j，那么p被重新分配给Oi；

第二种情况：p当前隶属于中心对象Oj。如果Oj被Orandom所代替作为中心点，且p离Orandom最近，那么p被重新分配给Orandom；

第三种情况：p当前隶属于中心对象Oi， i≠j。如果Oj被Orandom所代替作为中心点，而p仍然离Oi最近，那么对象的隶属不发生变化；

第四种情况：p当前隶属于中心对象Oi， i≠j。如果Oj被Orandom所代替作为中心点，且p离Orandom最近，那么p被重新分配给Orandom。

下面介绍一种典型的k-中心点算法PAM（Partitioning Around Medoids——围绕中心点划分）。

（1） PAM算法基本步骤：

①为找到k个簇，PAM方法为每个簇选择一个代表样本，即中心点。

②选定中心点后，其余样本被分配给与它最相似的中心点，更确切地说，若Oj是非代表对象，而Oi是一个中心点，若d（Oj， Oi）=minOed（Oj， Oe），则Oj属于Oi所代表的簇，这里d（Oj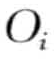， ）表示样本Oj和Oi的距离，minOe表示与所有中心点Oe的最小距离。

③簇的质量用样本与簇的中心点的平均距离来度量。

为了寻找k个中心点，PAM首先任意选择k个样本，然后每次用非代表样本Oh来代替代表对象Oi以改进聚类的质量。为了计算替代的效果，PAM将为所有非代表样本Oj计算Cjih，根据Oj属于的簇，Cj ih由下面等式中的一个决定：

第一种情况：假设Oj当前属于Oi所代表的簇。Oj， 2是离Oj第二相似的中心点。而且，与Oh相比Oj与Oj， 2更相似，即d（Oj， Oh）≥d（Oj， Oj，2）。因此，若Oh代替Oi成了中心点，Oj将属于由Oj，2代表的簇。那么，关于Oj的交换代价为：

这个等式将得到一个非负的Cjih，表示用Oh代替Oi是一个非负的代价。

第二种情况：假设Oj当前属于Oi所代表的簇。但是与Oh相比，Oj与Oj， 2相似度要小，即d（Oj， Oh）＜d（Oj， Oj，2），因此，若Oh代替Oi成了中心点，Oj将属于由Oh代表的簇。那么，关于Oj的交换代价为：

与式3-29不同的是，Cjih可以是正的也可以是负的，这要看Oi与Oh相比，哪个与Oj更相似。

第三种情况：假设Oj当前不属于Oi所代表的簇，而是属于由Oj，2代表的簇。而且，与Oh相比，Oj与Oj， 2更相似，即d（Oj， Oh）≥d（Oj， Oj， 2）。因此，若Oh代替Oi成了中心点，Oj将留在由Oj，2代表的簇。即交换代价为：

第四种情况：假设Oj当前属于由Oj， 2代表的簇。但是与Oh相比，Oj与Oj， 2相似度要小，即d（Oj， Oh）＜d（Oj， Oj，2）。因此，若Oh代替Oi成了中心点，Oj将属于由Oh代表的簇。那么，关于Oj的交换代价为：

这个等式得到的值总是负数。

综合以上四种情况，用Oh代替Oi总的代价和TCih为：

（2） PAM算法评价：PAM算法对小的数据集合非常有效，但对中等和大数据集没有良好的可伸缩性。在算法的第2，3步中，共有k×（n—k）对Oi， Oh。每一对计算TCih时，需要检查（n—k）个非代表对象。那么第2，3步的时间复杂度为O（k（n—k）2），而这只是一次循环的时间复杂度。因此，明显可以看出若n和k很大的话，PAM的代价将非常大。为了处理较大的数据集合，于是出现了CLARA算法作为PAM算法的补充。

CLARA不像PAM算法那样为整个数据集找出代表对象，而是选择数据集的一小部分作为数据的样本，然后对这些数据样本应用PAM方法来找到样本的中心点。如果样本是以非常随机的方式选取的，那么从这些样本中得出的中心点很可能与从整个数据集合中得到的中心点非常相似。为了得到更好的近似，CLARA将抽取数据集合的多个样本，对每个样本应用PAM算法，返回最好的聚类结果作为输出。在这里，评价聚类质量的度量是计算整个数据集中所有对象的平均相异度，而不仅是样本中的对象。

CLARA算法处理大数据集的执行结果是令人满意的。PAM每次循环的时间复杂度是O（k（n—k）2），而CLARA是对样本应用PAM算法，每次循环的时间复杂度为O（k（40 +k）2+k（n—k））。由此可以看出，处理大数据集时，CLARA算法比PAM算法迅速。