基于MapReduce的序列模式挖掘算法优化策略

无论是基于支持度框架的序列模式挖掘算法或是基于效用值框架的高效用序列模式挖掘算法，当面对大规模数据集的输入时，算法的运行效率会严重下降，并且在大数据环境下，算法无法在单机上完成挖掘的任务。面对大数据环境和单机性能瓶颈的问题，目前已有一些使用MapReduce框架实现的基于支持度框架的序列模式挖掘算法的研究成果（参见http://mahout.apache.org/users/misc/parallel-frequent-pattern-mining.html ）［12］。下面介绍MapReduce框架实现基于效用值框架的高效用序列模式挖掘算法。该方法采用效用矩阵、随机映射策略和基于领域知识的剪枝策略。效用矩阵用于过滤无用的单项序列、产生序列候选项；随机映射策略用于均衡计算量；基于领域知识的剪枝策略用于过滤序列候选项。

效用矩阵将q-序列以矩阵形式存储，通过对矩阵序列化和压缩的操作降低存储空间；此外，效用矩阵还可用于过滤无用的单项序列并产生序列候选项。表3-21为q-序列＜［（b， 2）（e， 2）］［（a， 7）（d， 3）］［（a， 4）（b， 1）（e， 2）］＞的效用矩阵。其中表3-21中（0，50）表示q-itemset 1中没有项a，剩余效用值为50。

表3-21　q-序列效用矩阵

根据效用矩阵，给出单项序列效用值上界与松弛率的定义。

定义3.36（单项序列效用值上界）：若序列t只含项i，那序列t的可用效用值表示为uremai（nt）=∑s∈s（ u res（t i ，s） + u（ i ，q） ），urest（i ， s）为项i对q-序列s的最大剩余效用值，u（i， q）为取得最大剩余效用值时，项i的效用值，uremain（ t ）为单项序列t效用值的上界。

定义3.37（松弛率）：给定效用值的阈值ξ，当且仅当uremain（t） ≥u·ξ， u ≥1时，称单项序列t为可用的单项序列，u称为松弛率。当u = 1时，若不是以t为起始的序列模式，那么这些序列模式结果不可能是高效用序列模式。

在MapReduce过程中，采用效用矩阵可快速提取可用的单项序列。利用可用的单项序列集合，过滤q-序列数据库中的单项序列，避免无用的单项序列产生候选项时带来系统资源的消耗和算法效率的降低。候选项的产生可以通过效用矩阵、项集内拼接和序列间拼接完成。

随机映射策略以均衡每一个分组中的序列数，防止单个分组计算资源消耗过大，充分利用集群的计算能力为目的。基于Random（K）的随机分配算法为每一个q-序列s分配键值，均衡地将q-序列数据库S中所有的q-序列进行分组，均衡集群中节点的任务数量。合理地分配分组中q-序列s的数量，不仅可以加快算法执行效率，同时还可以防止单个计算节点出现内存溢出的现象。

1）剪枝策略

（1）基于序列结构复杂度的剪枝：在拼接的过程中，拼接效用值高且剩余效用值高的前M个项。

序列候选项的结构复杂度和尺度与q-序列相关。复杂的q-序列会产生很多的序列候选项，降低查询的效率，同时结构复杂的序列候选项得出的序列模式不易于解释。因此基于实际应用中结构简单的模式易于解释的领域经验，通过控制M的大小来控制序列模式结构的复杂度。

（2）基于q-序列的尺度的剪枝：若候选项的尺度达到N，则停止拼接。

当给定一个q-序列数据库S，最大尺度为L。挖掘所有尺度小于等于L的候选项集合为CL，则CL的容量为|CL |，所需时间为TL；挖掘所有尺度小于等于N的候选项集合为CN，则CN的容量为|CN |，所需时间为TN。因为TN ＜ TL，令λ=| CL|—| CN|/|CL|，若λ＜β， β∈ （0， 1）成立，则称N为算法可接受的序列模式长度，其中λ为算法的模式丢失率，β为算法的容忍率。该剪枝策略以牺牲覆盖率的方式来换取时间效率的提升。

这两种剪枝策略组合起看，通过限制条件来挖掘特定的序列模式，并且序列模式结果集是可接受的。(www.xing528.com)

2）算法并行化

基于序列效用值的定义可知，序列t的效用值与q-序列数据库里每个q-序列s有关，若序列t匹配到q-子序列s′，取umax（s′），最后累加得到序列t的umax（t）。

这种批处理式的计算模式非常适合使用MapReduce框架。整个过程采用逆向实现，q-序列s使用效用矩阵产生序列候选项，得到所有的q-子序列s′和umax（s′）， q-子序列s′反向替代序列t，累加所有的um（ax s′），得到umax（t）。图3-31中给定输入q-序列数据库S，经过三次MapReduce过程并行计算高效用序列模式，最后将结果输出。

（1）步骤1：可用的单项序列生成：将S分片，每个Map将输入的q-序列s作为value，构建value的效用矩阵，得出每个单项序列t的urest（ i， s）+u（i， q）后以键值对形式输出。在Reduce端，输入为＜t， List ＜ urest（i， s） + u（i， q）＞＞，合并List中的值，得到序列t的可用效用值，若大于阈值ξ，则输出该单项序列t。具体算法步骤如图3-32所示。

（2）步骤2：候选项生成：将S分片，每个Map将输入的q-序列s作为value，用随机映射策略确定s的键值作为Map输出的键，s作为输出的值；这样Reduce端得到的输入为＜outkey， List＜s＞＞，之后Reduce端利用可用单项序列的信息，结合UtilityMatrix（s）的方法可生成相应经过剪枝后的候选项＜s′，umax（s′）＞的集合，最后合并输出到文件系统。具体算法步骤如图3-33所示。

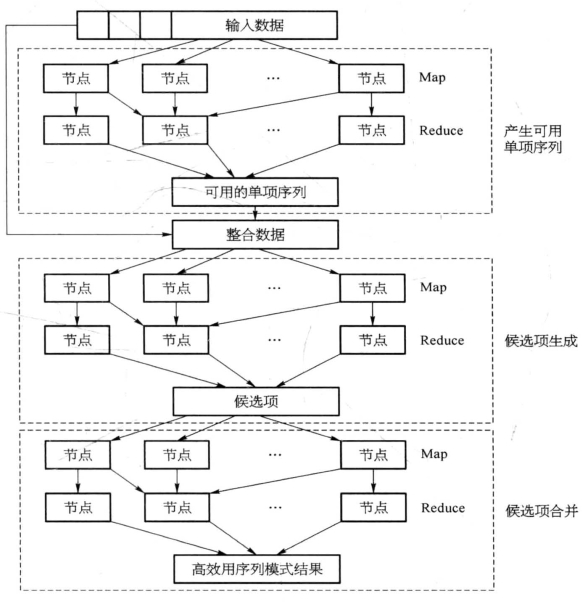
图3-31　基于MapReduce的高效用序列模式挖掘算法框架图

图3-32　步骤1可用单项序列生成算法

图3-33　步骤2候选项生成算法

（3）步骤3：合并候选项：步骤2中S生成了很多候选项，候选项可表示为＜t， utility＞，每个Map以此为输入，经过Map处理后形成输出＜t， List＜utility＞＞作为Reduce端的输入。根据umax（ t ）式子，输出结果以＜t， umax（t） ＞的形式写入文件系统。具体算法步骤如图3-34所示。

图3-34　步骤3合并候选项算法