前面章节已经介绍的基础算法(Apriori算法、FP-Growth算法、PrefixSpan算法等)是基于支持度框架的,即算法输出的模式是依据模式出现的频繁程度是否超过一定支持度阈值的。这种基于支持度框架的频繁模式(序列模式)挖掘方法忽略了模式的其他信息,在一些应用(尤其是商业领域)中可用性和可解释性方面都存在一定的局限。例如,表3-19中的项a, b,c等,表示某个电子商务网站销售的商品,第二行对应的数字2,5,4等,表示对应商品a,b,c等的利润(或价格)。表3-20表示购买这些商品的客户的交易序列。对于商家而言,他们不仅关注哪些商品被频繁购买了,还关注这些商品被一起购买产生的利润。因此,仅仅看商品是否频繁购买是不够的,需要引入一个“效用”(utility)的概念,例如,表3-20中,交易序列2中的e和a两种商品的组合<ea>的utility是{(6×1+1×2),(6×1+2×2)}={8, 10},<ea>在整个数据库里的utility是{{ },{8,10},{ },{16,10},{15, 7}}。我们在每个序列中选择最高的utility,那么<ea>的最高utility是10+16+15=41。如果这个值超过阈值,那<ea>作为输出模式,这样的结果反映了该商品组合所带来的总利润。本节介绍基于效用值的序列模式挖掘算法USpan[9]。
表3-19 单项利润表

表3-20 客户交易序列数据库

下面先给出相关的定义:
定义3.28(权重函数):每个项ik都有一个权重函数p(ik),即效用值。
定义3.29(q-项与q-项集):有序对(i, q),其中i∈I,q表示量(quality),称(i, q)为q-项;l=[(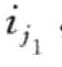 , q1), (
, q1), (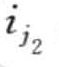 ,q2 ),…(
,q2 ),…(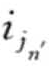 ′,
′,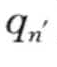 ],称l为q-项集(I为所有项的集合)。′
],称l为q-项集(I为所有项的集合)。′
定义3.30(q-序列与q-序列数据库): s = < l1 , l2 , …, lm >,称s为q-序列;S是元组〈sid, s〉的集合,成为q-序列数据库,其中sid表示序列编号,s表示一个q-序列。
定义3.31(q-项集包含与q-序列包含):给定两个q-项集la=[(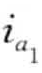 1 ,
1 , 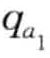 ),(
),( 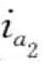 ,
,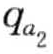 ),…(
),…(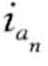 ,
,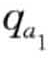 )]和lb=[(
)]和lb=[(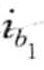 ,
,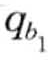 ) , (
) , ( ,
, 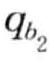 ),…(
),…(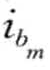 bm,
bm,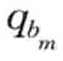 )],当且仅当存在一
)],当且仅当存在一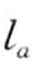 组整数1≤j1≤… ≤jn≤m,使得
组整数1≤j1≤… ≤jn≤m,使得 =
=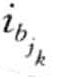 ∧
∧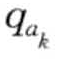 =
=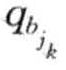 , 1 ≤ k ≤n,称l
, 1 ≤ k ≤n,称l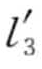 b包含la,记为
b包含la,记为 lb。
lb。
给定两个q-序列s=<l1, l2, l3, …, lm>和s′=<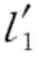 ,
, 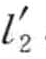 , , …,
, , …, 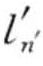 ′>,当且仅当存在一组整数1 ≤ j1 ≤ …≤ jn ≤ n′使得
′>,当且仅当存在一组整数1 ≤ j1 ≤ …≤ jn ≤ n′使得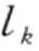
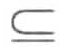
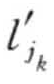 , 1 ≤ k ≤ n,称s′包含s,记为s
, 1 ≤ k ≤ n,称s′包含s,记为s s′ 。
s′ 。
定义3.32(匹配):给定一个q-序列s=< (s1, q1)(s2, q3)…(sn, qn ) >和一个序列t =〈t1t2…tm〉,当且仅当n = m且sk=tk, 1≤k≤n,称s匹配t,记t~s。
定义3.33(q-项、q-项集、q-序列与q-序列数据库的效用值)
记u(i,q) = 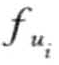 (p(i), q)为(i, q)的效用值,称为q-项效用值;(https://www.xing528.com)
(p(i), q)为(i, q)的效用值,称为q-项效用值;(https://www.xing528.com)

其中定义3.33中的函数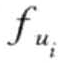 ,
, ,
,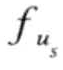 ,
,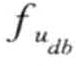 与应用相关,一般均为领域专家给出。
与应用相关,一般均为领域专家给出。
定义3.34(序列效用值):给定q-序列数据库S,序列t的效用值记为![]()
![]() ,其中
,其中![]()
定义3.35(高效用值序列模式):给定一个序列t,由于在一个q-序列s中可能会匹配多个s′,即有多个效用值u(s′),取最大值作为t关于s的效用值。若给定效用值的阈值ξ,当且仅当umax(t)≥ζ时 ,称序列t为高效用值序列模式。
其中umax(t)可以表示为![]()
USpan算法由Lexicographic Q-sequence Tree(LQS-Tree)[11]、两种拼接策略和两种剪枝策略组成:
(1) LQS-Tree主要用于构建和组织q-序列和它的效用值列表。
(2)拼接策略分为项集内拼接(I-Concatenated)和序列间拼接(S-Concatenated),如序列<(ab)>的项集内拼接为<(abc) >,序列间拼接为<(ab)c >。
(3)剪枝策略分为宽度剪枝(Width Pruning)和深度剪枝(Depth Pruning),宽度剪枝依据促进规则进行剪枝,LQS-Tree中一个节点,若节点拼接了新项不能促进效用值的增长,那么就不允许拼接,深度剪枝依据节点和拼接的新项的效用值的上界来限制,LQS-Tree在深度方向的增长。
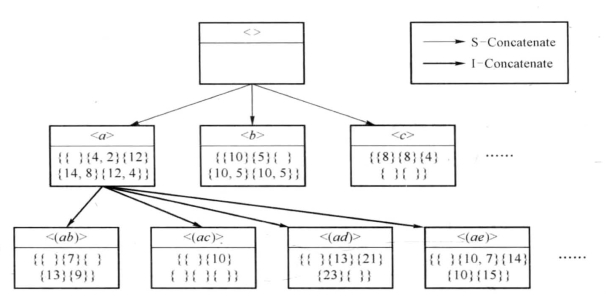
图3-29 LQS-Tree和拼接方式示意图[9]
根据图3-29可以发现,如果不使用剪枝策略,那么基于LQS-Tree和两种拼接方式的方法,会将q-序列数据库中的记录生成一棵庞大的LQS-Tree,导致搜索空间指数级的膨胀,算法效率严重下降。因此加入剪枝策略后,USpan算法如图3-30所示(更详细的介绍参见文献[10])。

图3-30 USpan算法
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




