序列模式挖掘算法优化探究

序列数据挖掘可以在一个序列中进行也可以在多序列中进行。序列数据常常表现为时间序列和空间序列两种形式，但本质上，两者是一致的，只是表示形式上两者分别由时间点或空间点及其对应的值组成。为统一时间点和空间点的表示以达到两者从形式和本质上都是统一的，引入一个新属性“序”，用以表示序列中元素对应的时间点或空间点，由此，将序列数据源定义如下：

定义3.19（单序列，single sequence）：单序列是一个包含n个形如（序，值） （ order，value）这样的偶对元素依照一定顺序排列的集合，记作：＜（X1，Y1），（X2，Y2）， …，（Xn，Yn）＞。其中， （Xi，Yi） （1≤i≤n）是序列中的元素，称为序元；Xi （1≤i≤n）是序元的序（order），表示时间或空间信息；Yi（1≤i≤n）是序元的值（value），特别的，Yi可以是多个对象的情况，甚至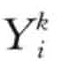还可以是复杂对象。

例3.10：某一客户在一段时间内使用信用卡的消费序列：＜（6月1日，预订机票）， （6月2日，预订酒店），（6月3日，租车服务）＞是一个单序列，“6月1日”等表示序元的序，机票、酒店等表示序元的值，值（“机票”）又可对应复杂对象：｛票价，时间，出发地点，目的地｝。

定义3.20（M-序列，multiple sequences）： M条同类的单序列组成的有限序列集，称为M-序列，记为：

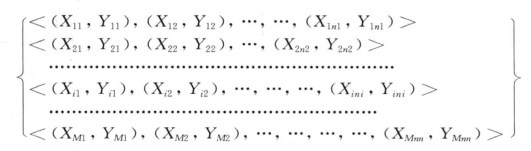
其中，Xini为相同类型的序；Yini为同类型的值，i表示M-序列中的第i条序列，ni表示第i条序列具有ni个元素，即其长度为ni（1≤i≤M，M是正整数），特别地，当M=1时，M序列退化为单序列；当M＞1时，它表示多序列。由于M-序列中各单序列长度不一定相等，因此，第i条序列的长度ni可以同于或不同于第j条序列的长度nj。

注意，在上下文清楚的情况下，序“Xini”也可省略。

定义3.21（子序列，subsequence）：一条单序列T=＜（x1，t1），（x2，t2），…，（xm，tm）＞是M-序列中某一单序列S= ＜（Xi1，Yi1） ， （Xi2， Yi2），…，… ，… ，（Xini，Yini）＞的子序列（m≤ni），满足下面条件：对于每一个j， 1≤j≤m—1，有xj＜x（j+1），且对于每一个j，1≤j ≤m，存在1≤l1 ＜l2＜…＜ln≤m，使得t1Yil1，t2Yil2 ， …，tmYilm，则称序列T为S的子序列，S为T的超序列。

定义3.22（序列模式，sequential pattern）：满足一定出现频率（用户指定的阈值）的子序列称为序列模式。

定义3.23（M-序列模式挖掘，M-sequences sequential pattern mining）：在M-序列中找出满足一定出现频率的所有子序列（即找出所有序列模式）的过程称为M-序列模式挖掘。

序列模式挖掘过程一般包括以下几个阶段：排序阶段、发现频繁项集阶段、转换阶段、序列阶段以及最大阶段（基于多支持度的序列模式挖掘过程也包括类似的阶段，在后面的介绍中将略去其中某些阶段，重点集中在序列阶段挖掘算法的介绍）。

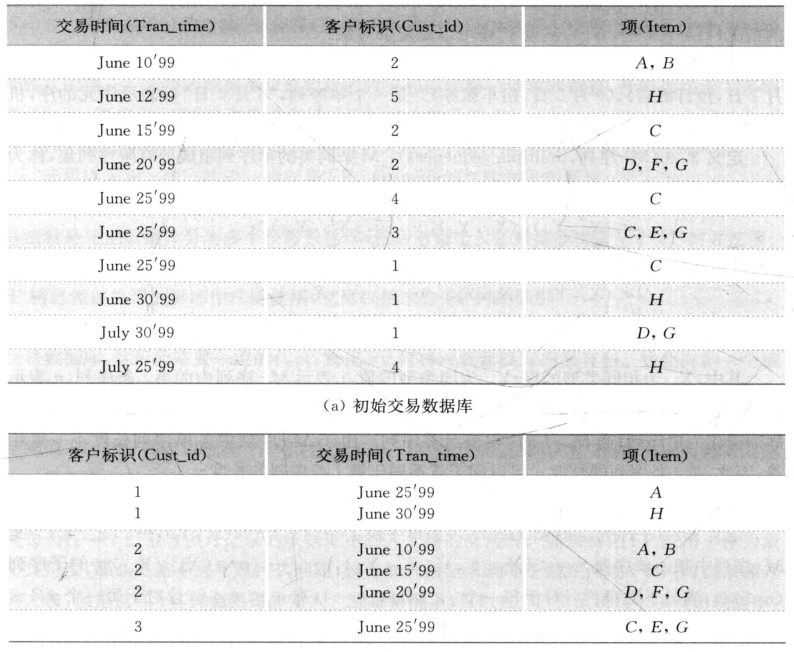
（1）排序阶段。利用客户标识作为主关键字、交易发生的时间作为次关键字对初始交易数据库（见表3-7a）排序得到按关键字排序后的数据库（见表3-7b），并将原始的交易数据库转换成客户序列的数据库（见表3-7c）。

表3-7　排序阶段数据库

（续表）

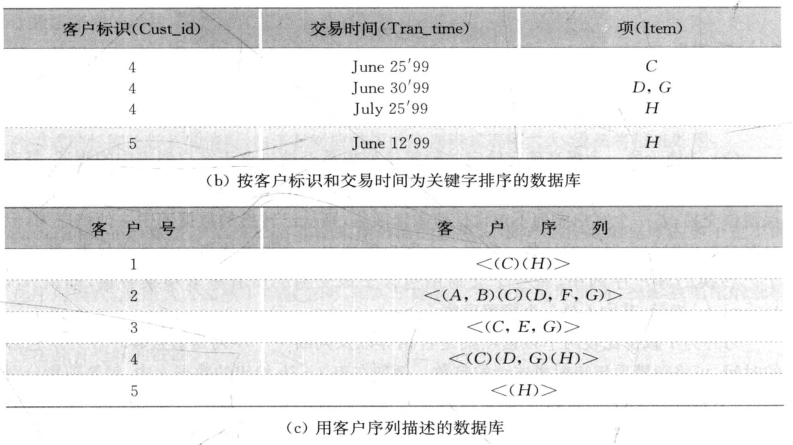
（2）发现频繁项集阶段。基于单支持度定义的序列模式挖掘算法主要考虑模式在每一序列中出现与否，子序列T的支持度定义为在多序列中包含T的序列数，即若子序列T在多序列的某一序列中出现则加1，否则不变。在这种支持度定义下，序列模式挖掘的是被包含在足够多条序列中的模式，而不考虑子序列在每一序列中重复出现的次数。

如果一单序列S（或子序列）不包含在任何其他单序列之中，则称该单序列（或子序列）为极大序列（或极大序列模式）。注意，序列模式挖掘除了发现极大序列模式外，另外还有挖掘闭合序列模式的［5］，以及针对极大和闭合两类模式平衡问题的研究（既考虑模式也考虑支持度的平衡）［6］。

表3-6c中，设最小支持度阈值为25%（也就是最小支持2个客户），存在＜（C）（H）＞和＜（C）（D， G）＞两个序列模式，因为它们在那些满足支持度阈值的序列中是极大的。序列模式＜（C）（H）＞被客户1和客户4所支持。客户4在项C和项H之间购买了项＜（D）（G）＞，但仍然支持模式＜（C） （H） ＞，这是因为所找的模式并不需要一定连续。序列模式＜（C）（ D， G）＞被客户2和客户4所支持。虽然客户2在购买项D和项G的同时购买了F，但仍然支持这个模式，因为（D， G）是（D， F， G）的一个子集。

序列＜（A， B）（C）＞是一个低于最小支持度阈值的模式，它只被客户2所支持。而序列＜（C）＞，＜（D）＞，＜（G）＞，＜（H）＞，＜（C）（D）＞，＜（C）（G）＞以及＜（D， G）＞虽然具有最小支持度，但它们不是极大的，因为它们包含在＜（C）（H）＞或＜（C） （D， G）＞中。最后得到表3-8的结果（因为比较频繁项集耗时一定，形成单独的数据库可以减少检查一个序列是否被包含于一个客户序列中的时间）。

表3-8　序列模式集合

（3）转换阶段。为提高确定给定的频繁序列集是否被包含于客户列表中的测试，需对每一个客户序列进行转换。如果一个交易不包含任何频繁项集，则在已转换的序列中不应保留该交易；若一个客户序列不包含任何频繁项集，则从已转换的数据库中去掉该序列，但总客户数仍对包含对它的计数。最终一个客户序列由一个频繁项集的序列来代表，即在一个已转换的客户序列中，每一个交易用包含于该交易的所有频繁项集替换，即由｛l1，l2，… ，ln｝表示，其中li是一个频繁项集。

另外为了减少比较两个频繁项集是否相等以及判断一个序列是否被客户序列所包含的时间，可将频繁项集映射成连续的整数。例如在表3-7b给出的数据库中，频繁项集分别是（C）、（D）、（G）、（D， G）和（H），可以将其分别映射为连续的整数1、2、3、4和5。经过映射以后，可以将频繁项集按一个实体的形式进行处理，使得比较和处理更加方便高效。将客户序列数据库转换如表3-9所示。例如，在对ID号为2的客户序列进行转换的时候，交易（A， B）被剔除了，因为它并没有包含任何频繁项集；交易（D， F， G）则被频繁项集的集合｛（D），（G），（D， G）｝代替。

表3-9　转换后的数据库

（4）序列阶段。在这一阶段，要利用已得到的频繁项集的集合来找到所有的频繁序列。目前已有多种方法实现频繁序列的挖掘，包括类Apriori的序列挖掘模式挖掘的三种算法—A—prioriAl l、AprioriSome和DynamicSome算法［7］。AprioriAll算法多次遍历数据库，在每一次遍历中，利用上一次遍历产生的频繁序列来产生候选序列，并在遍历过程中计算它们的支持度。在遍历的最后，候选序列的支持度用来决定其是否为频繁序列（剔除低于支持度阈值的候选序列）。该算法由于需要计数许多非极大序列，因而性能较差。AprioriSome算法与DynamicSome算法都针对AprioriAll算法的缺点做了适度的优化，这两个算法都分成多个阶段分别计算，从而减少非极大序列的计数，但是由于同时增加了对非频繁序列的计数，因此并不能显著地提高算法的性能。

又如引入时间与概念层次约束的GSP（generalized sequential patterns）算法，更加灵活地挖掘各种序列模式［8］。GSP算法存在的主要问题有三个：第一，如果序列数据库的规模比较大，则有可能会产生大量的候选序列模式；第二，需要对序列数据库进行循环扫描：第三，对于序列模式的长度比较长的情况，由于其对应的短的序列模式规模太大，算法将很难处理。

上述这些算法都是基于类Apriori算法。由于需要频繁扫描数据库并且计算大量的候选序列，因此整体效率都不高。之后研究者提出了PrefixSpan（ prefix-project sequential pattern mining）算法，PrefixSpan算法采用分治的思想，不断产生序列数据库的多个更小的投影数据库，然后在各个投影数据库上进行序列模式挖掘。PrefixSpan算法不需要产生候选序列模式，从而大大缩减了检索空间，相对于原始的序列数据库而言，投影数据库的规模不断减小，PrefixSpan算法的主要开销在于投影数据库的构造。该算法比各种类Apriori算法具有更好的性能。

后面将给出上述几种主要算法的详细描述。

（5）最大阶段。在频繁序列中发现极大序列（一般算法为减少对非最大序列计数过程时间的耗费将最大阶段算法与序列阶段混合在一起）。假定在序列阶段已经找到所有频繁序列的集合S后，下述算法（图3-18）可以用来找出极大序列（定义最长序列的长度为n）：

图3-18　发现极大序列算法

前面已经介绍了Apriori性质，这个性质同样可用于序列模式挖掘［7，8］：若长度为k的序列模式是非频繁的，其超集（长度为k+1）不可能是频繁的。因此，序列模式的方法之一也是采用类Apriori算法的变种，但所考虑的参数设置和约束有所不同。类Apriori算法的基本流程是：对数据库进行多次遍历，第一次扫描序列数据库，生成长度为1的频繁子序列。每次遍历中，将前一次生成的序列模式作为下一次的种子集合（seed set），利用这个种子集合生成新的潜在模式，即候选序列（candidate sequences），并计算这些候选序列的支持度，再将支持度大于等于最小支持度阈值的候选序列作为下一次的种子集合，算法反复进行，直到不再产生新的序列模式。

所使用的算法有两种不同的计数策略—c—ount-all和count-some。count-all方法对所有频繁序列计数，包括非极大序列，这些非极大序列在最大化阶段将被删除。AprioriAll算法基于count-all策略寻找频繁序列。AprioriSome与DynamicSome算法基于countsome策略——由于仅关心极大序列，如果先计数更长的序列，则可以避免计数那些被包含在更长序列里的短序列。

另一种挖掘序列模式的方法是基于数据库投影的序列模式增长计数，类似于无候选生成的频繁模式挖掘的频繁模式增长（FP-Growth）算法。

1） AprioriAll算法详述

AprioriAll算法在每一次数据库遍历中，利用上一次遍历得到的频繁序列来产生候选序列，并在遍历过程中计算它们的支持度。在遍历的最后，删除低于最小支持度阈值的候选序列，得到频繁序列。在第一次遍历时，频繁项集阶段的输出被用来初始化频繁1-序列的集合。

寻找频繁序列的AprioriAll算法流程如图3-19所示。

图3-19　AprioriAll算法

算法中Lk代表所有长度为k的频繁序列组成的集合，Ck代表长度为k的候选序列组成的集合。

在上述算法中，从Lk-1生成新的候选序列Ck过程由apriori-generate函数实现，函数apriori-generate将所有的长度为“k-1”的频繁序列的集合Lk—1作为参数，包括两个步骤：

第一步，对Lk—1做自连接，如图3-20示：

图3-20　Lk-1做自连接

第二步，对于c∈Ck，如果存在c的长度为“k—1”的子序列不包含于Lk—1之中，则删除c。

一个频繁序列的任何子序列都必须满足最小支持度，因此，若用所有可能的频繁项集来扩充Lk—1中的每一个序列，然后删除那些所有不在Lk-1中的长度为“k—1”的子序列，将得到一个在Lk中的序列的超集，即CkLk 。

在表3-10所示，考察第一列中显示的L3，当由它生成C4时，在自连接结束后，得到第二列所示的结果，进一步删除那些子序列不在L3中的序列，第三列显示的序列将被保留。例如序列＜1243＞由于它有一个子序列＜243＞不在L3中，所以被删除。

表3-10　候选序列生成过程

下面来看一个AprioriAll算法的具体实例。考察表3-11所示的由客户序列组成的数据库，在这里没有给出源数据库的形式。客户序列以转换的形式出现，每一笔交易都被其包含的频繁项集所取代，频繁项集则映射为整数。最小支持度定义为40%（即至少支持两个客户序列）。对数据库的第一次遍历在频繁项集阶段进行。图3-21显示了每次遍历最后阶段所得到的频繁序列和它们的支持度。最后得到的极大序列为＜1234＞、＜135＞和＜4 5＞ 。

表3-11　客户序列

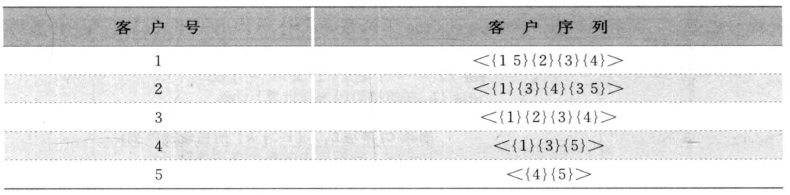
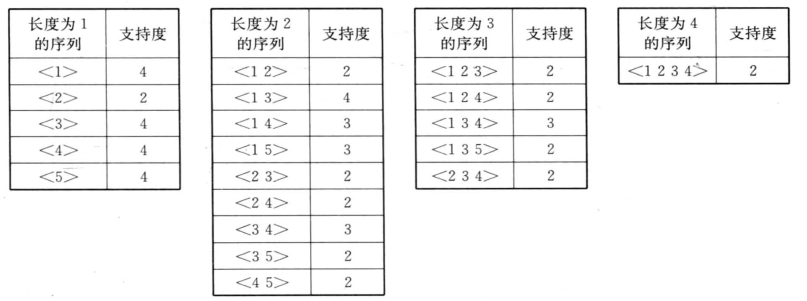
图3-21　频繁序列的产生

2） AprioriSome算法详述

AprioriSome是一种基于count-some策略的频繁序列发现算法。AprioriSome算法分为两个阶段：前推阶段（forward phase），寻找具有一定长度的所有频繁序列；回溯阶段（backward phase），寻找所有剩余的频繁序列。具体算法如图3-22所示：

图3-22　AprioriSome算法

在前推阶段中，只对特定长度的序列进行计数（即扫描数据库计算支持度）。next函数（图3-23）用于确定前推阶段应该对哪些序列进行计数。比如，前推阶段只对长度为1，2，4和6的序列计数，而长度为3和5的序列则在回溯阶段中计数。一种极端情形是next（k） =k+1（k为最后一次计数的候选序列的长度），在这种情况下AprioriSome算法退化为AprioriAll算法。此时虽然所有非极大序列都将被计数，但是由于每个Ck都是由Lk—1而不是Ck—1生成的，因此Ck的规模较小；而对另一种极端的情形，比如next（ k） =100k，这时几乎没有非极大序列被计算，但由于每个Ck都是由Ck-1生成（Ck-1较Lk-1大很多），因此Ck的规模将会很大。

选择的next函数应该对这两种情况折中以获得较好的性能。一种可能的next函数如下所示，其中hitk定义为频繁k-序列和候选k-序列个数之比，即|Lk|/|Ck|。

图3-23　next函数

在回溯阶段，对那些在前推阶段没有计数的序列进行计数，因为需要的是极大序列，所以可以删除那些包含在其他频繁序列中的候选序列（即Ck中的某些项）。同时可以删除那些虽然在前推阶段已经被计数，但是也包含于其他频繁序列中的序列（即Lk中的某些项）。

下面来看一个AprioriSome算法的实例，数据库如表3-11所示，取next（k） =2k。

在频繁项集阶段得到L1（图3-21），然后，遍历数据库对C2计数得到L2（图3-21），以L2作为输入参数调用apriori-generate函数产生C3，如表3-12所示。此时，不对C3计数，因此也不产生L3。下一步以C3作为参数调用apriori-generate直接产生C4，在经过计数与删除后，得到的结果与图3-21中L4相同。当试图产生C5时结果为空。

表3-12　候选3-序列

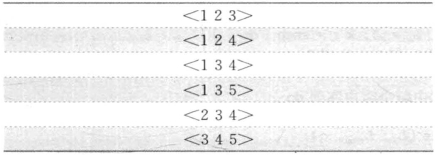
前推阶段完成后，进行回溯。L4中的序列不被删除，因为没有更长的序列了（即它不是其他序列的子序列）。在前推阶段没有对C3中序列的支持度计数。删除C3中那些是L4（＜1234＞）的子序列的序列之后，得到剩下的两个序列＜135＞和＜345＞。这两个序列计数后发现＜135＞是一个长度为3的最大频繁序列。下一步，除了＜45＞以外L2中所有的序列都被删除，因为它们都包含于某一个更长的序列中。同样的道理，L1中所有的序列都被删除了。

可以发现，对应AprioriAll算法对六个3序列计数，AprioriSome只对两个3序列计数，在AprioriAll算法中不计数的序列，AprioriSome算法也不对其计数。但在通常情况下，AprioriSome将某些小候选序列计数而AprioriAll不对其计数。例如从C3产生的C4就比从L3产生的C4大。

3） DynamicSome算法详述

DynamicSome算法虽然与AprioriSome算法基于相同的思想，即都是通过对序列采用分阶段计数策略来减少计算量，但与AprioriSome算法相比仍有较大的不同。DynamicSome算法分为四个阶段，用大于1的整型变量step来决定哪些候选项被计数。在初始化阶段，对所有C1， C2 ，…，Cstep计数生成L1，L2，…，Lstep。在前推阶段通过序列连接计算出所有的Ln·step（n=2，3，…），注意在这一阶段并没有计算任何Ck，这与AprioriSome算法是不同的。算法的回溯阶段调与AprioriSome算法相同，但是由于前推阶段没有计算任何Ck，因增加一个调整阶段用于生成候选序列。例如，在前推阶段计算出了L3和L6，计算L9时为空；由于此时没有任何候选集生成，于是调用调整阶段生成C7、 C8；随后在回溯阶段删除C7、C8中的非极大序列并依次对C7、C8进行计数。需要注意的是，在初始化阶段和调整阶段，算法使用与AprioriAll算法相同的候选项集生成方法；而在前推阶段使用otf-generate函数生成候选集。各个阶段的详细算法如图3-24（略去回溯阶段）所示。

图3-24　DynamicSome算法

前推阶段使用的otf-generate函数的输入参数为Lk、 Lj和客户序列c，根据这三个参数生成包含在c中的长度为（k+j）的候选序列。函数的思想是如果有两个序列sk ∈ Lk和sj∈Lj，当sk 、sj都包含于c中且不相互重叠，可以认为＜sk·sj＞是一个长度为（k+j）的候选序列。函数的具体实现如图3-25所示。

图3-25　otf-generate函数(www.xing528.com)

例如，假定otf-generate函数接受的三个参数为L2、L2和c，其中L2如图3-21中所示，c为＜｛1｝｛2｝｛3 7｝｛4｝＞。经过计算函数得到的序列及对应的end和start值如表3-13所示。最后连接的结果为＜1234＞。

表3-13　end和start值

上述的三种算法能有效地挖掘序列模式，AprioriAll算法采用count-all的计数策略，不可避免地要计数许多非极大序列；AprioriSome和DynamicSome算法虽然可以减少非极大序列的计数，但同时增加了对非频繁序列的计数。因此在性能AprioriAl l与AprioriSome算法上整体相差不多，而DynamicSome算法由于在前推阶段要计算大量的候选序列，因而性能稍差，这主要由otf-generate函数所决定。

但是，类Apriori算法过程中可能生成大量的候选序列，如有1000个频繁序列，长度为1，（＜a1＞＜a2＞…＜a1000＞），类Apriori算法需要生成的候选序列总数可达到10002 +1000×999/2；此外，类Apriori算法需要多遍扫描数据库：序列长度每次增长都需要扫描数据库，如要发现序列模式｛（abc）（abc）（abc） （abc）（abc）｝，算法需要扫描15遍数据库；类Apriori算法在生成长度较长的序列模式时效率较低：序列模式越长，所需要生成的序列就越多，例如，数据库中含有一个长度为100的单序列＜a1a2 …a100 ＞，最小支持度取1，则需要生成的候选序列，长度为2的有100×100+100×99/2=14950，长度为3的有，总数量超过

综上，类Apriori算法的瓶颈在于逐步生成和检验候选序列的过程，然而在许多应用中，如DNA分析、股票序列分析等，发现大量的序列模式和长序列模式是很常见的，因此，需要掌握更有效、伸缩性更好的方法。

下面介绍两种不需产生候选的伸缩性更好的基于单支持度定义的序列模式挖掘算法。

1） FreeSpan算法（Frequent pattern projected Sequential pattern mining）详述［9］

FreeSpan频繁模式投影的序列模式挖掘算法的基本思想是，反复使用频繁序列把序列数据库转换成更小的投影数据库。处理过程中，把检验的数据和频繁序列分区，确保每次检验后序列数据库都变小。

表3-14　例3.11序列数据库S

例3.11：序列数据库S如表3-14前两列所示，最小支持度设为2。第一次遍历序列数据库S，得出每个项的支持度计数，找到频繁项集L1，即长度为1的序列模式。频繁项按支持度降序排列形成频繁项列表，记为f_list：

f_list=＜b： 5，c： 4，a： 3，d： 3，e： 3，f： 3＞，其中b： 5表示（项：支持度）。

根据f_list， S的序列模式可被分为不相交的六个子集：①只包含项f；②包含项e，但不包含项f；③包含项d，但不包含项e和f；④以此类推……

然后，构造频繁项矩阵F计算由f list中的项生成的长度为2的序列出现的频率。对于f_list（i1， i2，…，in），F是一个三角矩阵F［j， k］（1≤j≤m，1≤k≤j）。其中F［j，j］（1≤j≤m）仅有一个计数值，而其他每个F［j，k］（1≤j≤m，1≤k≤j）有三个计数值： （A，B，C），其中A是ik在ij后出现的计数（即包含序列＜ijik＞），B是ik在ij前出现的计数（即包含序列＜ikij＞） ，C表示ik， ij同时出现的计数（即包含序列＜（ikij ）＞） 。

f_list中有六项，生成一个6×6三角频繁项矩阵（图3-26），各计数器初始化为0。第二次扫描填充矩阵。

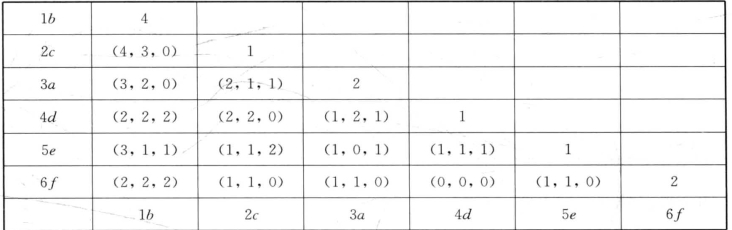
图3-26　F矩阵

例3.12：第一个序列＜（bd）cb（ac）＞，可知＜bc＞与＜cb＞出现，但＜（bc）＞不出现，因此F［b，c］=（1，1，0）；对于F［b， d］=（0，1，1），因为＜（bd）＞与＜db＞出现但＜bd＞不出现；以此类推，完全扫描序列数据库第二遍后得到图3-26。

对于项集X， X的投影数据库是含有X中所有项的序列的集合，其中，非频繁项以及在fl_ist中X后的项被删除。同样的，对于序列模式α，α的投影数据库是含有α的序列集的子序列，非频繁项及α后的项也被删除。

循环项模式标记形如，其中$…$表示两种形式＜…＞：仅查找指定顺序序列；｛…｝查找任何有序序列。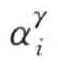有两种表示形式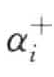： ： αi出现多次；αi ：αi没有重复出现（其中αi和αi中至少一个重复出现）。

投影数据库标记形如｝，其中$…$表示同上，｛bp，…，bq｝表示在子序列挖掘过程中与合在一起生成长度更长的序列模式的频繁项集。

根据以上设定，由频繁项矩阵生成长度为2的序列模式和投影数据库再产生长度为3以及更长的序列模式。步骤如下：

（1）生成长度为2的序列模式：如果计数值不小于最小支持度阈值，则输出相应的频繁模式。

（2）对每一行j在循环项模式上生成标记。

（3）对每一行j在投影数据库中生成标记。

标记生成后，可以不再考虑矩阵。基于从矩阵生成的标记，可以再次扫描数据库以生成循环项模式和投影数据库。下次过程递归挖掘每个更小的投影数据库。本例第三次数据库扫描得到循环项集模式（表3-15）。

表3-15　第三次数据库扫描得到循环项集模式

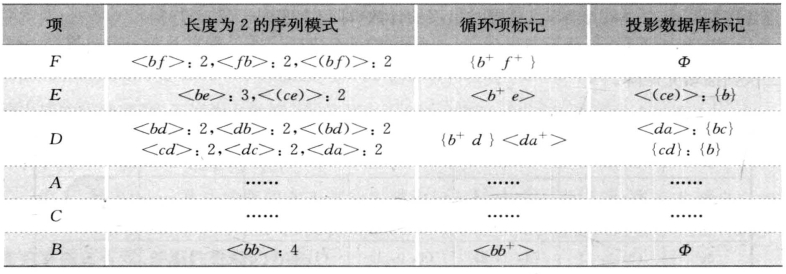
四个投影数据库如表3-16所示。

表3-16　四个投影数据库

（1）当投影数据库中的标记仅含三项，则所得的相关序列模式仅需扫描投影数据库即可得到。

（2）若超过三项，则构造频繁项矩阵并递归调用上述步骤。

FreeSpan算法如图3-27所示。

图3-27　FreeSpan算法

2） PrefixSpan算法详述

PrefixSpan（通过前缀投影挖掘序列模式）算法基本思想：序列数据库投影时，并不考虑所有可能出现的频繁子序列，而是基于频繁前缀，因为所有的频繁子序列都可以通过生成频繁前缀找到，不需要生成候选序列。

例3.13：有序列数据库，如表3-17所示。假设序列元素中的项以字母序排列。如序列标识为10的序列记作＜a（abc）（ac）d（cf）＞，而不写成＜a （bac）（ca） d （fc） ＞，根据这个约定，每个序列就有了唯一的表达形式。

表3-17　序列数据库

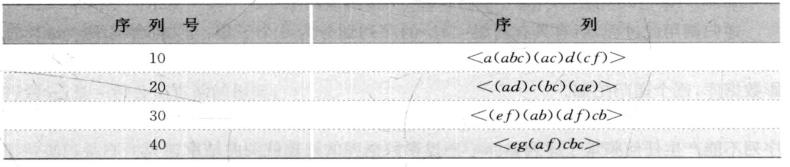
定义3.24（前缀）：给定序列α=＜e1， e2，…，en＞，β=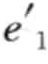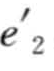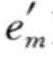＜，…， ＞（m≤n）。β为α的前缀，当且仅当中的所有项按字母序排列在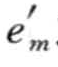之后。

定义3.25（关于前缀的投影）：给定序列α和β，其中β是α的子序列，即βα。 α的子序列α′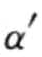（ α ）， α′被称为α关于前缀β的投影，当且仅当①β是α′的前缀；②不存在α的超集α″（即α′ 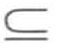α″， α′ ≠α″），使得α″是α的子序列并且β是α的前缀。

α′ =＜e1e2…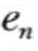＞是α关于前缀β = ＜ e1e2…em—1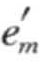＞的投影（m≤n）。γ=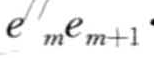＜…en＞是α关于前缀β的后缀，写作γ = α/β，其中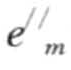， = （em—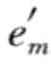），也可以记为α=β·γ。

如果β不是α的子序列，则α关于β的投影和后缀都为空。

例如，＜a＞，＜aa＞，＜a（ab）＞，＜a（abc）＞是序列＜a（abc）（ac）d（cf）＞的前缀，但是＜ab＞，＜a（bc）＞不是前缀。＜（abc）（ac）d（cf）＞是序列＜a（abc）（ac）d（cf）＞关于前缀＜a＞的后缀。＜（_bc）（ac）d（cf）＞是关于前缀＜aa＞的后缀。＜（_c）（ac）d（cf）＞是序列关于前缀＜ab＞的后缀。

序列数据库同表3-17的S，最小支持度为2，在序列数据库S中用前缀投影算法挖掘序列模式步骤如下：

步骤1：寻找长度为1的序列模式。第一次扫描序列数据库S，找到所有序列中的频繁项，每个频繁项即长度为1的序列。用“＜模式＞：计数”表达式表示模式及相关的支持数，得到＜a＞： 4，＜b＞ ： 4，＜c＞： 4，＜d＞： 3，＜e＞： 3，＜f ＞： 3。

步骤2：分割搜索空间。序列模式集可按6个前缀被划分为六个子集：包含前缀＜a＞的子集；……；包含前缀＜f＞的子集。

步骤3：寻找序列模式的子集。序列模式子集挖掘可以通过构建并递归挖掘投影数据库实现。最终发现的投影数据库和序列模式如表7-12中所示。挖掘过程解释如下：

首先，寻找具有前缀＜a＞的序列模式。只需要扫描含有＜a＞且＜a＞首先出现的序列。例如，对于序列＜（ef）（ab）（df）cb＞，挖掘具有前缀＜a＞序列模式时，只需考虑子序列＜（_b）（df）cb＞；又如：＜a（abc）（ac）d（cf）＞的子序列＜（abc）（ac）d（cf）＞需被考虑。

序列数据库S中包含＜a＞的序列被投影为关于＜a＞的＜a＞-投影数据库，由4个后缀序列组成：＜（abc）（ac）d（cf）＞，＜（_d）c（bc）（ae）＞，＜（_b）（df）cb＞，＜（_f）cbc＞。扫描＜a＞-投影数据库一遍，即可找到含有前缀＜a＞的长度为2的序列模式，包括：＜aa＞：2，＜ab＞： 4，＜（ab）＞： 2，＜ac＞： 4，＜ad＞： 2，＜af＞： 2。

递归调用此过程，所有具有前缀＜a＞的序列划分为6个子集：①包含前缀＜aa＞的子集；②包含前缀＜ab＞的子集；……；⑥包含前缀＜af＞的子集。这些子集通过建立投影数据库，逐个递归挖掘。

＜aa＞-投影数据库只包括一个非空（后缀）子序列：＜（_bc）（ac）d（cf）＞。由于一个序列不能产生任何频繁子序列，＜aa＞-投影数据库的处理就到此结束。

＜ab＞-投影数据库包含三个非空后缀子序列：＜（_c） （ac） d（ cf） ＞， ＜（_c）a＞，＜c＞。挖掘＜ab＞-投影数据库，返回4个序列模式：＜（_c）＞， ＜（_c）a＞， ＜a＞， ＜c＞（即＜a（bc）＞，＜a（bc）a＞，＜aba＞，＜abc＞）。

＜（ab）＞-投影数据库只包括两个非空（后缀）子序列：＜（_c）（ac）d（cf）＞，＜（df）cb＞，包含前缀＜（ab）＞的序列模式有：＜c＞，＜d＞，＜f＞，＜dc＞。

＜ac＞-，＜ad＞-，＜a f＞-投影数据库可以用相同的方法建立，挖掘找到的序列模式如表3-18所示。

同样的，也能找到前缀＜b＞-，＜c＞-，＜d＞-，＜e＞-，＜f＞-投影数据库，然后递归进行挖掘。结果显示如表3-18所示。

表3-18　投影数据库和序列模式

（续表）

引理3.5（ 分区）：设α是长度为l的序列模式（l≥0），｛β1， β2， …， βm｝是具有前缀α的所有长度为（l+1）的序列模式。包含前缀α的所有序列模式的集合，除α本身外，可被划分为m个不相交的子集。第j个子集（1≤j≤m）是含有前缀βj的序列模式。设Φ为所有序列数据库的默认序列模式。

基于引理3.5， PrefixSpan把问题分为递归的问题。即序列模式的每个子集必要时进行划分，是一种分而自治的框架。

定义3.26（投影数据库，projected database）：设α是序列数据库S中的序列模式，α-投影数据库是序列数据库S中关于前缀α的序列的后缀序列集合，记为S|α。

定义3.27（投影数据库的支持度计数）：设α是序列数据库S中的序列模式，β是具有前缀α的序列。β在α-投影数据库S|α的支持度计数是在投影数据库S|α中γ满足β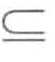α·γ的序列γ的数量，β记为supports|α（β ）。

注意：supports|α（）≤supports|α（β /α，例）：supports（ ＜（ad）＞） =1，然而，＜（ad）＞/＜a＞ = ＜d＞， support s|＜a＞s（＜d＞）= 3。

引理3.6（投影数据库）设α、β是序列数据库S中两个的序列模式，α是β的前缀。

（1） S |β =（S |α） |β。

（2）对于任何具有前缀α的序列γ， supports（ γ） = supports | α（ γ） 。

（3） α—投影数据库的大小不会超过S的大小。

基于上面的定义和定理，PrefixSpan算法如图3-28所示：

3）算法PrefixSpan

图3-28　PrefixSpan算法