挖掘量化关联规则的方法与技巧

描述量化（或数值型）属性之间的关系的规则称为量化关联规则。

例3.6（图3-5） ：如表People，具有三个属性：Age、 NumCars、 Married。前两个为量化属性，第三个为类别属性。可以得到一条量化关联规则，如（Age=“30，…，39”） ∧（Married=Yes）（NumCars=2）。

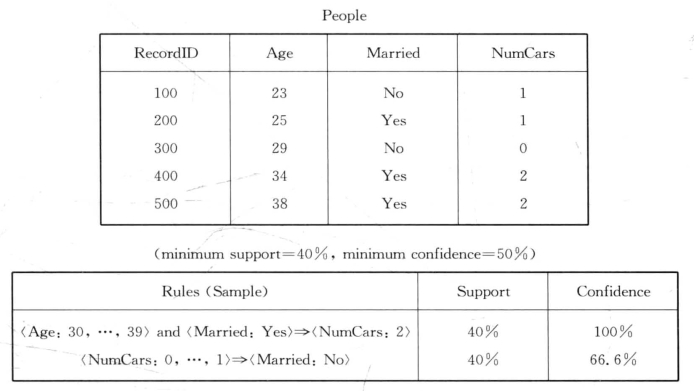
图3-5　量化关联规则示例

挖掘量化关联规则常用的方法是将连续数据离散化，从而把量化关联规则的问题转换成布尔型关联规则的问题进行讨论。

当全部属性取值数量都是有限的时候，如上例中属性“汽车数量（NumCars） ”（0，1，2），只需将每个属性值映射为一个布尔型的值即可，这种映射是直观的，对应（attribute= value）表示若attribute在原始记录中有值为value，则其布尔值为1，否则为0；当属性的取值范围很宽时（即量化属性值域很大时），则需将其分为若干个区间，然后将每个区间映射为一个布尔型属性，如“年龄（age） ”，则分为两个区间（20，…， 29）和（30，…，39），于是对应记录（Age=23），有“Age： 20，…，29=1”，而“Age： 30，…，39=0”。图3-5映射为布尔型关联规则问题后，如图3-6所示，然后用布尔关联规则挖掘算法进行挖掘。

图3-6　映射为布尔型关联规则问题

图3-7说明了由图3-5中的具有离散属性的原始数据中挖掘量化关联规则的分解步骤，最终得出合适的量化关联规则。

图3-7　量化关联规则问题分解示例

量化关联规则挖掘步骤：

第一步，决定每个量化属性的划分数量。

（1）对每个类别属性，将属性值映射到连续的整数集上，如属性Married，具有两个值“Yes”和“No”，将其分别映射到“1”和“2”。

（2）对每个量化属性，没有划分为对应区间的，将值映射到满足预先定义值序的连续整数上；若已划分区间的量化属性，将值映射到连续整数上（按预先定义的值序）。

第二步，为每个量化和类别属性计算支持度。注：对量化属性，当其支持度小于最小值支持度阈值时，可将邻接值合并，至此，找到所有具有最小支持度频繁1项集。(www.xing528.com)

第三步，采用类似简单关联规则挖掘算法生成频繁项集（如类Apriori算法的生成候选，包括自连接和子集剪枝，产生长度更长的频繁项集）。

第四步，采用关联规则挖掘第二个步骤（由频繁项集到关联规则的生成）得到相应的量化关联规则。

例3.7：如表People。量化关联规则挖掘过程如下：

将Age属性划分为四个区间，如图3-7b所示，则图3-7a可映射为图3-7c。

将区间映射为连续整数值，如图3-7d所示，则图3-7a可映射为图3-7e。

假设min_sup= 40%， min_conf=50%。

图3-7f给出了一些频繁项集，图3-7g给出了一些量化关联规则。

图3-7g和3-7f用原始表中的值替换映射的值。

可以发现，＜Age： 20，…， 29＞对应＜20，…， 24＞和＜25，…， 29＞区间的连接，即量化属性的更好的划分区间可以在必要时连接合并邻接区间。

通过前面的描述和例子，概括地说，处理量化属性的具体方法有以下几种：

（1）量化属性根据数据的分布分成了一些布尔属性。每个布尔属性都表示一个量化属性的区间，落在其中则为1，反之为0。这种分法是动态的。得出的规则常被称为布尔量化关联规则，如图3-5到图3-6的映射。

（2）使用预定义的概念分层对量化属性进行离散化。离散化在挖掘之前，区间是由用户预先定义的，如年龄的概念分层可以分为区间，“20，…， 29”、“30，…， 39”、“40，…， 49”等替换原来的数值。得出的规则称为静态量化关联规则，如图3-7b所示。

（3）量化属性被分成一些能体现它含义的区间。这种方法考虑数据之间的距离因素。得出的规则称基于距离的量化关联规则。

量化属性进行映射时的难点主要在于可能存在以下两个问题：

（1）最小支持度问题：如果量化属性区间数量（或属性未被划分为区间时的值）太大，则任何单个区间的支持度都将会较低。因此，缺乏大区间使得包含该属性的规则由于低于最小支持度而无法发现。即当区间范围太窄时，可能使每个区间对应的属性的支持度很低，而出现“最小支持度问题”。

（2）最小置信度问题：当区间范围太宽，可能使每个区间对应的属性的置信度很低，例图3-6中，（NumCars=0（Married= No），其置信度为100%，但若将NumCars的值0，1划分为同一区间，则规则（NumCars=0，…，1 （Married= No），其置信度为66%。