挖掘简单关联规则技巧大揭秘

1）第一种方法：基于Apriori性质有候选生成的Apriori算法

单维、单层、布尔型是最简单形式的关联规则，挖掘简单关联规则最有影响力的算法之一是使用候选项集寻找频繁项集算法——Apriori算法（详细算法请参见3.3.1节）。

首先给出一个重要的性质——Apriori性质：一个频繁项集的任何非空子集也一定是频繁项集（即如果长度为k的项集在数据库中是非频繁的，那么长度为k+1的项集在数据库中也不可能是频繁的）。

Apriori算法基本思想：使用逐层搜索的迭代方法，利用Apriori性质，反复的从长度为k的频繁项集中得到长度为k+1的候选项集，进一步由此产生长度为k+1的频繁项集。

算法需要对交易数据库进行多遍扫描，具体过程如下：在第一次扫描中，计算单个项的支持度，并且将超过最小支持度阈值的项作为频繁项集，在后续的每一次扫描中，利用上一轮扫描产生的频繁项集作为种子项集（seed set），产生候选项集，进一步确定频繁项集，并把它们作为下一次扫描的种子项集。这个过程一直进行，直到不能找到新的频繁项集。

由频繁（k—1）-项集（种子项集）产生频繁k-项集的迭代过程由连接和剪枝两个步骤实现。

（1）连接步：通过频繁（k—1）-项集与自己连接产生候选k-项集的集合。

（2）剪枝步：通过候选k-项集的集合确定频繁k-项集（利用Apriori性质压缩候选k-项集）。

一般情况，在扫描数据库的过程中对第一步产生的候选项集的支持度进行计数，扫描结束时，支持度大于指定最小支持度阈值的候选项集被确定为频繁项集。但由于候选项集是最终所得频繁项集的超集，其成员可能是频繁的也可能是不频繁的，若每次扫描数据库都通过计算候选项集中的支持度计数来确定频繁项集，则可能由于候选项集过大，造成计算量过大，为减少候选集的数量，压缩搜索空间，利用Apriori性质［任何非频繁的（k—1）-项集都不可能是频繁k-项集的子集性质］，判定候选项集中的候选项是否频繁，即使用判断标准：若一个候选k-项集的（k—1）-子集不在频繁（k—1）-项集中，则该候选也不可能是频繁的，从而可将其从k-项集的集合中删除，由此一定程度地减少了候选项集的数量，相应地减少计算支持度的次数。

例3.5：如表3-2中的交易数据库D。给出Apriori算法的实际计算过程，如图3-2所示。

在此，为简单起见，支持度用项集出现的次数表示，而不以百分比形式表示，本例中设最小支持度阈值为2。

其中Lk表示频繁k-项集，Ck表示候选k-项集。

候选1-项集C1中的各项集支持度均大于等于最小支持度阈值，于是频繁1-项集L1中包含所有C1中的项集。

频繁1-项集L1与L1进行自连接得到候选2-项集C2： ｛I1， I2 ｝、｛I1， I3｝、｛I1， I4｝、｛I1， I5｝、｛I2， I3｝、｛I2， I4 ｝、｛I2， I5｝、｛I3， I4｝、｛I3， I5｝、｛I4， I5｝，其子集均在L1中，不需剪枝，再对所有候选进行计数，｛I1， I4｝、｛I3， I4｝、｛I3， I5｝、｛I4， I5｝支持度小于最小支持度阈值，不是频繁2-项集，其余都是频繁的。

频繁2-项集L2与L2进行自连接得到候选3-项集C3： ｛I1， I2， I3｝、｛I1， I2， I5｝、｛I1， I3， I5｝、｛I1， I3， I4｝、｛I2， I3， I5｝、｛I2， I4， I5｝，但后面四个候选不可能是频繁的，因为｛I3， I5｝、｛I3， I4｝、｛I4， I5｝均不在L2中，将其剪枝，再对前两个候选进行计数，得到频繁3-项集L3。

图3-2　Apriori算法的计算过程

3-项集L3与L3进行自连接得到候选4-项集C4：｛I1，I2，I3，I5｝，但其子集｛I1， I3，I5｝不在L3中，将其剪枝。

最后由算法得出频繁项集为：｛I1： 6｝、｛I2： 7｝、｛I3： 6｝、｛I4： 2｝、｛I5： 2｝、｛I1， I2：4｝、｛I1， I3： 4｝、｛I1， I5： 2｝、｛I2， I3： 4｝、｛I2， I4： 2｝、｛I2， I5： 2｝、｛I1， I2， I3： 2｝、｛I1，I2， I5： 2｝，注，冒号（：）后表示各频繁项集的支持度。

2）第二种方法：不产生候选挖掘频繁项集

Apriori算法采用的“候选产生-检查”方法大幅度压缩了候选项集的大小，得到较好的性能，然而Apriori算法产生大量候选项集及对数据库的多次扫描也产生了大量的开销。

FP-Growth（频繁模式增长）算法是一种具有更好性能和伸缩性的频繁项集挖掘算法，其主要特点是不需要生成大量候选项集。算法采用分而治之的策略：第一次扫描交易数据库，与Apriori算法第一步相同，收集单个项的支持度，并且将超过最小支持度的项作为频繁项集（1-项集）；然后构造一个独特的、压缩的数据结构：频繁模式树（frequent-pattern tree，简记FP-Tree），用于存储关于频繁模式的关键信息；再将频繁模式树分化成一些条件库（一种特殊类型的投影数据库），每个条件库和一个频繁项相关，再对这些条件库分别进行挖掘。

定义3.18（频繁模式树）：一棵频繁模式树是一个如下定义的树结构（图3-3）：它有一个标记为“null”的根节点，其子节点是一系列的项前缀子树（item prefix subtree），还包括一个频繁项头表（frequent-item header table）。

（1）项前缀子树的每个节点由三个部分组成：项名（itemn-ame）、项计数（count）、节点链（node-link），项名表示节点所代表的项，项计数表示在这条路径上到达这个节点的交易的数量，节点链指向EP树中具有相同项名的下一个节点，如果不存在节点，则设为null 。

（2）频繁项头表的每个条目由两个部分组成：项名（itemn-ame）和节点链头（head of node-link），节点链头指向FP树中表示这个项名的第一个节点。

频繁模式树的设计与构造过程如下：(www.xing528.com)

在此不给出详细的算法描述及证明过程（详见3.3.4），仅用一个具体的例子来更形象地说明FP树的构造过程。假设有一个交易数据库D，如表3-3所示，设最小支持度阈值为3。

表3-3　交易数据库D

首先，第一次扫描数据库可以得到频繁项列FList： ＜（f：4）， （c：4），（a：3），（b：3），（m：3）， （p：3）＞（冒号以后的数字表示支持度）。每个项按照出现的次数降序排列，这个次序很重要，因为树的每条路径都符合这个次序。为了方便后面讨论，每个交易的频繁项都按照这种次序排列，如表3-3中第三列所示。

创建树的根结点，标记为null。然后开始第二次扫描数据库，并对每个交易创建一个分支。

扫描第一个交易时，得到树的第一个分支：＜ （f： 1）， （c： 1）， （a： 1）， （m： 1）， （p： 1） ＞。注意交易中的频繁项按照频繁项列FList的次序排列。扫描第二个交易，因为它的频繁项列为＜f，c，a，b，m＞，和已有的路径＜f，c，a，m，p＞共享了一个共同的前缀＜f，c， a＞，所以前缀中的每个节点计数都增加1；并且需要创建两个新节点，先创建新节点（b：1），作为已有节点（a： 2）的子节点，再创建新节点（m： 1），作为新节点（b： 1）的子节点。对第三个交易，因为它的频繁项列＜f，b＞和前缀子树f共享了节点＜f＞，所以f的计数加1，并且创建一个新节点（b： 1），作为节点（f： 3）的子节点。对第四个交易的扫描，得到树的第二个分支＜（c： 1），（b： 1），（p： 1）＞。对最后一个交易，因为它的频繁项列＜f，c，a，m，p＞和第一个交易相同，所以该路径上的每个节点计数都增加1。

为了方便树的遍历，建立项的头表，头表中的每个项通过节点链头指向该项在树中的出现位置。通过这个节点链，将具有相同项名的节点按序链接在一起。

扫描所有的交易后，最终得到一棵与节点链关联的树，即FP树构造完成，结果如图3-3所示。

图3-3　由表生成的FP树

当FP-树构造完成后，对数据库频繁项集的挖掘问题就转换成挖掘FP-树问题。

本节中FP-树的挖掘同样用一个具体的例子来说明（详细算法见3.3.4节）。如图3-3中所示的FP树，频繁模式根据FList（＜（f： 4），（c： 4），（a： 3），（b： 3），（m： 3），（p： 3）＞）可以被划分为若干个子集：包含p的模式，包含m但不包含p的模式， …，包含c但不包含a，b，m，p的模式，包含f但不包含c，a，b，m，p的模式等。于是挖掘过程首先对节点p，可以得到一个频繁模式（p： 3）和FP树中的两条路径：＜f： 4，c： 3，a： 3，m： 2，p： 2＞，＜c： 1， b： 1， p： 1＞。第一条路径表示串“（f，c，a，m，p）”在数据库中出现两次，尽管串＜f， c， a＞出现了三次，＜f＞出现了四次，但它们和p一起出现的次数是两次。因此考虑和p同时出现的串，可以得到符合条件的p前缀路径＜f： 2， c： 2， a： 2， m： 2＞。同样的，第二条路径表示串“（c， b， p）”在数据库的交易中只出现一次，p的前缀路径是＜c：1，b： 1＞。 p的这两条前缀路径｛（f： 2， c： 2， a： 2， m： 2），（c： 1， b： 1）｝组成了p的子模式库，称为条件模式库（conditional pattern base）（即在p存在时的子模式库）。在这个条件模式库上建立的FP树（称为p的条件FP树，conditional FP tree），只生成了一个分支（c： 3），因为其他支持度计数小于最小支持度计数（已设为3），如f的支持度为2。最后只得到一个频繁模式（c，p： 3）。至此，查找和p有关的频繁模式结束，得到两个频繁模式： （p： 3）和（cp： 3）（需要注意的是，一个模式是一个项集，在这里用一个串表示）。

对节点m，可以得到一个频繁模式（m： 3）和FP树中的两条路径：＜f： 4，c： 3，a： 3，m： 2＞， ＜f： 4， c： 3， a： 3， b： 1， m： 1＞。虽然p和m是一起出现的，但在这里分析时不需要考虑p，因为包含p的频繁模式已经在前面分析过。和前面分析过程类似，m的条件模式库为｛（f： 2， c： 2， a： 2），（f： 1， c： 1， a： 1， b： 1） ｝。在这之上构造FP树，得到m的条件FP树＜f： 3， c： 3， a： 3＞，是一个单独路径，然后对m的条件FP树进行递归挖掘，用mine （＜ f： 3， c： 3， a： 3＞| m）表示，过程如图3-4所示。

m的条件FP树挖掘过程包括三项： （a）， （c）， （f）。由此，除m本身外（即频繁模式m： 3），对于（a），得到第一个含有m的频繁模式：am ： 3，对应am的条件模式库为｛（fc：3）｝，再递归挖掘，即mine（＜f： 3， c： 3＞|am）；对于（c），得到第二个含有m的频繁模式：cm ： 3，对应cm的条件模式库为｛（f： 3）｝，再递归挖掘，即mine（＜f： 3＞|cm）；对于（f），得到第三个含有m的频繁模式：fm： 3，无对应条件模式库，不需递归挖掘。

再来看递归挖掘过程：mine（＜f： 3， c： 3＞ | am），生成两个模式cam ： 3和fam ： 3，以及一个条件模式库｛（f： 3） ｝ ，于是递归挖掘，即mine（＜f： 3＞ | cam），得到最长的模式fcam： 3；同样的，对于mine（＜f： 3＞ | cm），得到一个频繁模式fcm： 3。

因此，包含m的所有频繁模式的集合有：｛ （m： 3） ， （am： 3） ，（cm： 3），（fm： 3），（cam：3），（fam： 3），（fcam： 3），（fcm： 3）｝，如图3-4所示。

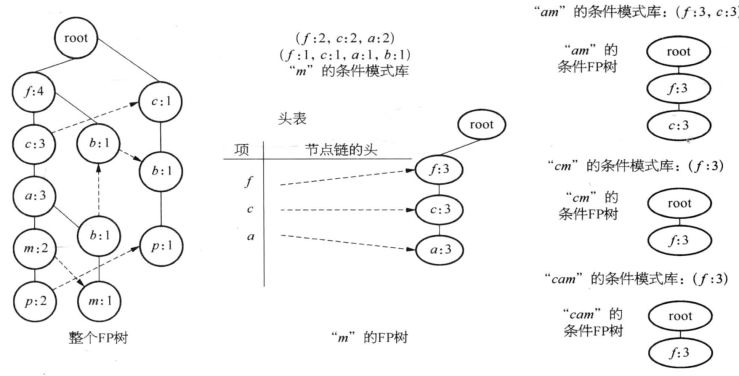
图3-4　“m”的条件FP树，即“FP树|m”

容易发现，对一个单独路径的FP树进行挖掘时，可以通过输出该路径上所有项的组合来实现。

类似的，由节点b可以得到（b： 3）和三条路径＜f： 4， c： 3， a： 3， b： 1＞， ＜f： 4， b：1＞， ＜c： 1， b： 1＞。因为b的条件模式库｛ （f： 1， c： 1， a： 1）， （f： 1），（c： 1）｝没有生成频繁项，挖掘结束。而由节点a得到一个频繁模式（a： 3）和一个子模式库｛ （f： 3，c： 3） ｝，这是一个单路径的FP树，因此，它的频繁模式集可以由组合得到。将它们和（a：3）相连，得到｛ （fa： 3）， （ca： 3）， （fca： 3） ｝。从节点c得到（c： 4）和一个子模式库｛ （f：3） ｝，得到一个与（C： 3）关联的频繁模式集｛ （fc： 3） ｝。而从节点f只得到（f： 4），它没有条件模式库。

条件模式库和条件FP树的生成可以见表3-4所示的说明。

表3-4　创建条件模式库来挖掘所有模式

算法采用基于分区的分治法，在相对于原始数据库要小很多的树上进行，避免了扫描庞大的数据库，有效地降低了搜索空间。另外，当原始数据量很大的时候，也可以结合划分的方法，使得一个FP-tree可以放入主存中。对比FP-Growth与Apriori的性能可以发现，FP-Growth比Apriori具有明显的性能提升，FP-growth对不同长度的模式都有很好的适应性，挖掘的模式越长，两个算法性能的差异越大。

用以上两种算法挖掘到频繁项集后，采用关联规则挖掘第二个步骤（由频繁项集到关联规则的生成）得到相应的简单关联规则。