纯电容电路的特性和应用

把电容器接到交流电源上，如果电容器的漏电电阻和分布电感可以忽略不计，这种电路叫作纯电容电路，如图3.3.9 所示。

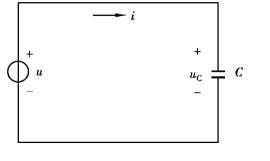
图3.3.9　纯电容电路

（1）电流、电压间数量关系

电容元件是储能元件，把从电路中吸收的能量转化为电场能储存起来，在一定条件下又放出能量送回电路。其电压与电流成正比，即

式中　UC——电容器两端电压的有效值，单位是伏[特]，符号为V；

　　　I——电路中的电流有效值，单位是安[培]，符号为A；

　　　XC——电容的电抗，简称容抗，单位是欧[姆]，符号为Ω。

上式叫纯电容电路的欧姆定律。容抗表示电容器对电路中的交流电流所呈现的阻碍作用。

将式（3.3.14）两端同时乘以，得

这说明纯电容电路中，电流、电压的最大值也服从欧姆定律。

理论和实验证明，容抗的大小与电源频率成反比，与电容器的电容成反比。容抗的公式为

式中　f——电源频率，单位是赫[兹]，符号为Hz；

　　　C——电容器的电容，单位是法[拉]，符号为F；

　　　XC——电容器的容抗，单位是欧[姆]，符号为Ω。

对直流电，它的频率f=0，则XC趋于无穷大，可视为断路。对交流电，当它的频率f 上升时，则容抗XC减小。故电容器具有通交流、阻直流的特点。

根据电容器的电容定义式C=，可以得到电荷量的变化与电容和电压变化的关系式：

则纯电容电路中的电流为

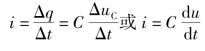
可根据上式，仿照纯电感电路电流、电压相位关系的分析方法，得出结论：纯电容电路中电流相位超前电压相位

设电容器两端的电压为

则电路中的电流为

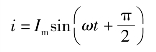
电流、电压的波形图和旋转矢量图分别如图3.3.10 和图3.3.11 所示。

（2）纯电容电路的功率

纯电容电路的瞬时功率等于电压瞬时值与电流瞬时值之积，即

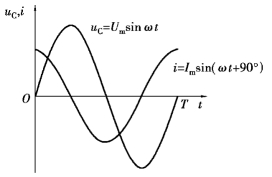
图3.3.10　纯电容电路电流、电压波形图(www.xing528.com)

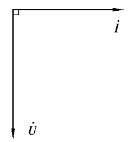
图3.3.11　纯电容电路电流、电压旋转矢量图

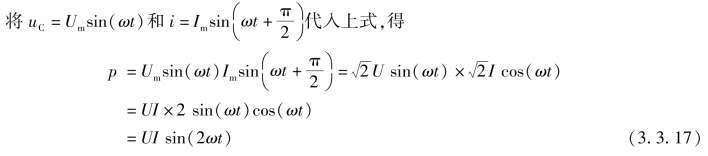
由上式可以看出，纯电容电路的瞬时功率P 是随时间按正弦规律变化的，它的频率为电压（或电流）频率的2 倍，振幅为UI，波形图如图3.3.12 所示。从图中可以看出，纯电容电路的有功功率为零，这说明纯电容电路不消耗电能。

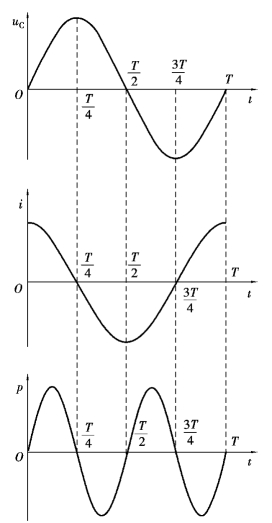
图3.3.12　纯电容电路功率曲线

同纯电感电路相似，虽然纯电容电路不消耗能量，但是电容器和电源之间进行着能量交换。在0～这两个周期内，由于电压uC 与电流i 同为正值或同为负值，瞬时功率p 为正值。由于电压的绝对值是增加的，电容器充电，电场能量增加。这说明在这两个周期内，电容器把电源提供的电能转换成电容器中的电场能量，电容器起负载的作用，相当于吸收能量。在T～T 这两个周期内，由于电压uC与电流i 一个为正值一个为负值，瞬时功率p 为负值。由于这时电压的绝对值减小，电容器放电，电场能量减少。电容器把原来储存的电场能量还给电源。为了表示电容器与电源能量交换的多少，把瞬时功率的最大值叫作纯电容电路的无功功率，即

式中　UC——电容器两端电压有效值，单位是伏[特]，符号为V；

　　　I——电路中电流有效值，单位是安[培]，符号为A；

　　　QC——容性无功功率，单位是乏，符号为var。

电容性无功功率的公式也写成

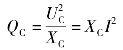
通过以上讨论，可以得出如下几点结论：

①在纯电容电路中，电流和电压是同频率的正弦量。

②电流i 与电压的变化率成正比，电流超前电压

③电流、电压最大值和有效值之间都服从欧姆定律。电压与电流瞬时值因相位相差

，但不服从欧姆定律，要特别注意：

④电容是储能元件，它不消耗电功率，电路的有功功率为零。无功功率等于电压有效值与电流有效值之积。

⑤平均功率（有功功率）P

结论：在正弦交流电路中，纯电容元件不消耗能量，只和电源进行能量交换（能量的吞吐）。

例3.3.3 已知：C=1 μF，求电容电路中的电流：电流有效值I、瞬时值i，画出电压、电流向量图。

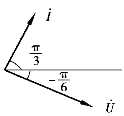
图3.3.13　向量图

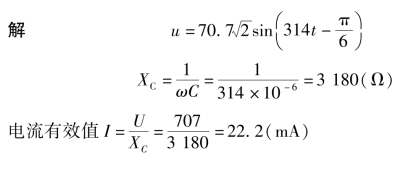
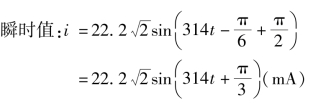
例3.3.4 设有一电容器，其电容C=38.5 μF，电阻可忽略不计，接于50 Hz、220 V 的电压上。

试求：该电容的容抗；电路中的电流I 及其与电压的相位差；电容的无功功率。若外加电压的数值不变，频率变为5 000 Hz，重求以上各项。

解 XC=1/（2πfC）=80 Ω；

电流有效值为I=U/XC=2.75 A，电流相位超前电压90°；

无功功率Q=UI=605 var；

当频率增大到原来的100 倍，容抗减小为原来的1/100；电流、无功功率增大到100 倍。