数控编程规则详解

数控编程中统一规定了机床坐标轴及其运动方向，是为了便于描述机床的运动，简化程序的编制，并使所编程序具有通用性。

1.坐标轴及运动方向

目前，国际标准化组织规定统一使用标准坐标系（ISO841），我国机械工业部也颁布了JB3051—1999《数控机床坐标系和运动方向的命名》的数控标准，它与ISO841标准等效。这些命名原则和规定是：

（1）刀具相对于静止的工件而运动的原则

为了使编程人员能够在不知道机床加工零件时是刀具移向工件，还是工件移向刀具的情况下，就可以根据零件图样确定工件的加工过程，特规定这—原则。

（2）标准坐标系的规定

标准坐标系也叫机床坐标系。在编制程序时，以该坐标系来规定运动的方向和距离。国际标准化组织（ISO）统一规定采用右手直角笛卡儿坐标系作为数控机床的标准坐标系，如图2-12所示。

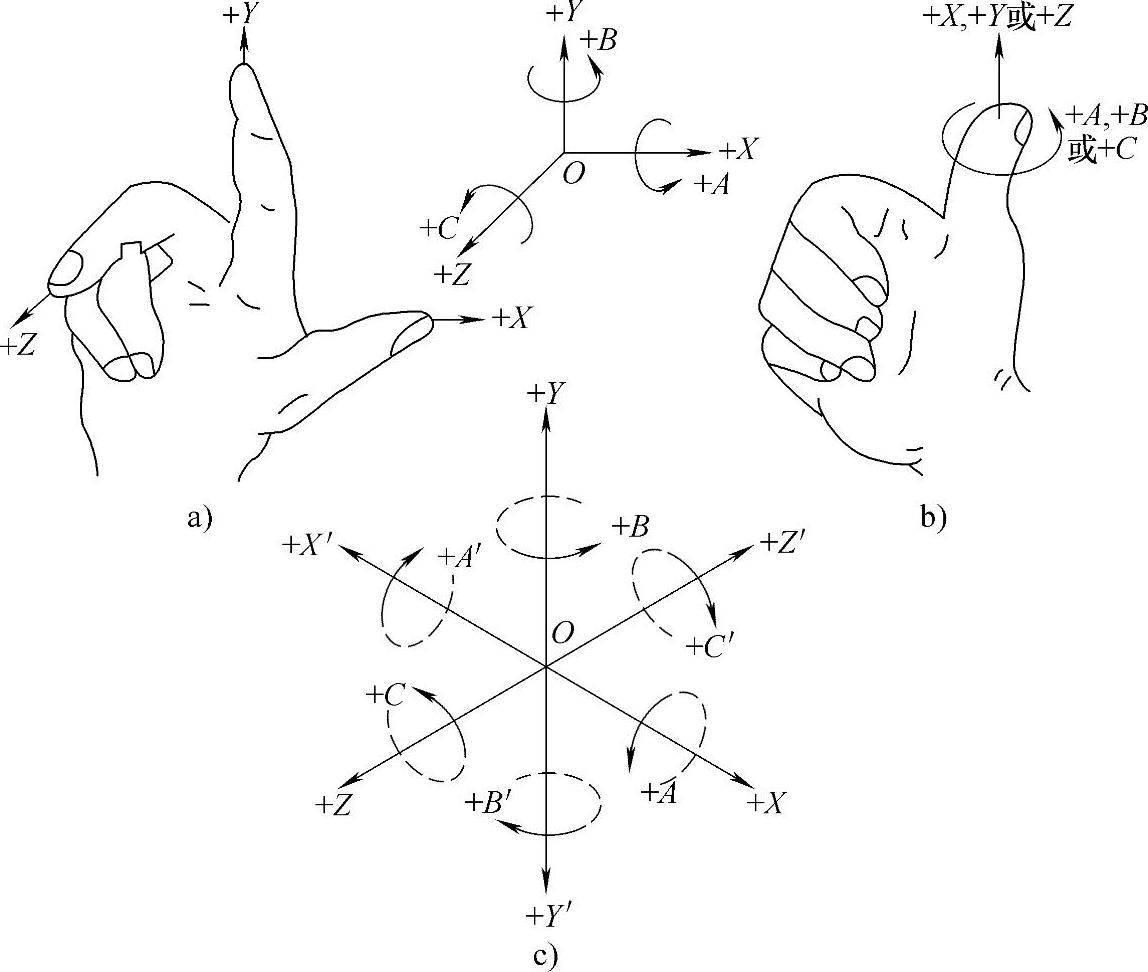
图2-12 右手直角笛卡儿坐标系

在图2-12中，大拇指的指向为X轴的正方向，食指的指向为Y轴的正方向，中指的指向为Z轴的正方向。该坐标系的各坐标轴与机床主要导轨相平行。—般来说，工件安装在机床上，要按机床的主要直线导轨找正工件。

通常在命名或编程时，在机床加工过程中，不论是刀具移动还是被加工工件移动，都一律假定被加工工件是相对静止的，刀具是移动的。所以，图2-12中的X、Y、Z、A、B、C的方向是指刀具相对移动的方向。

如果把刀具看成是相对静止的，工件是相对移动的，则用X′、Y′、Z′、A′、B′、C′的方向来表示工件相对移动的方向。由图2-12可见，X和X′、Y和Y′、Z和Z′等的方向是相反的。

（3）运动方向的确定

坐标轴定义顺序是先确定Z轴，然后确定X轴，最后确定Y轴。

JB3501-1999中规定：机床某一运动部件的运动正方向，是增大刀具和工件之间距离的方向。

①Z坐标的运动

Z坐标的运动由传递切削力的支轴决定，与机床主轴轴线平行或重合的坐标轴即为Z坐标。对于铣床、锤床、钻床等主轴带动刀具旋转的轴是Z轴；对于车床、磨床和其他加工旋转体的机床，主轴带动工件旋转，Z轴与主轴旋转中心重合，平行于床身导轨。

Z坐标的正方向为增大刀具与工件之间距离的方向。如在钻镗加工中，钻入或镗入工件的方向为Z坐标的负方向，退出方向为正方向。

②X坐标的运动

X坐标是水平的，是平行于工件的装夹表面，它是刀具或工件定位平面内运动的主要坐标。

对于工件做旋转运动的机床（如车床、磨床等），X坐标的方向平行于横向滑座，在工件的径向上，刀具远离工件的方向为X轴正方向。对于刀具做旋转运动的机床（如铣床、钻床等），若Z轴是水平的（主轴是卧式的），沿刀具、主轴后端向工件方向看，X轴的正方向指向后方；若Z轴为垂直的（主轴是立式的），则面对刀具、主轴向立柱方向看，新方向即为X轴的正方向。

③Y坐标的运动

Y坐标轴垂直于X和Z坐标轴。Y轴正方向根据X轴和Z轴的正方向，按右手笛卡儿直角坐标系来确定。

（4）旋转运动A、B和C

A、B、C分别为绕X、Y、Z轴转动的旋转轴，其方向根据右手螺旋法则来判定。

（5）其他坐标轴

一般靠近主轴的坐标系为第一坐标系，稍远的且分别与X、Y、Z轴平行的U、V、W坐标轴称为第二坐标系，如果再有分别与X、Y、Z坐标轴平行的轴，则称第二坐标系P、Q、R坐标轴。其他不平行于X、Y、Z坐标轴的，取名为D轴或E轴等。

（6）数控机床的坐标简图

图2-13～图2-24所示为几种常见数控机床的标准坐标系。

图2-13 数控车床

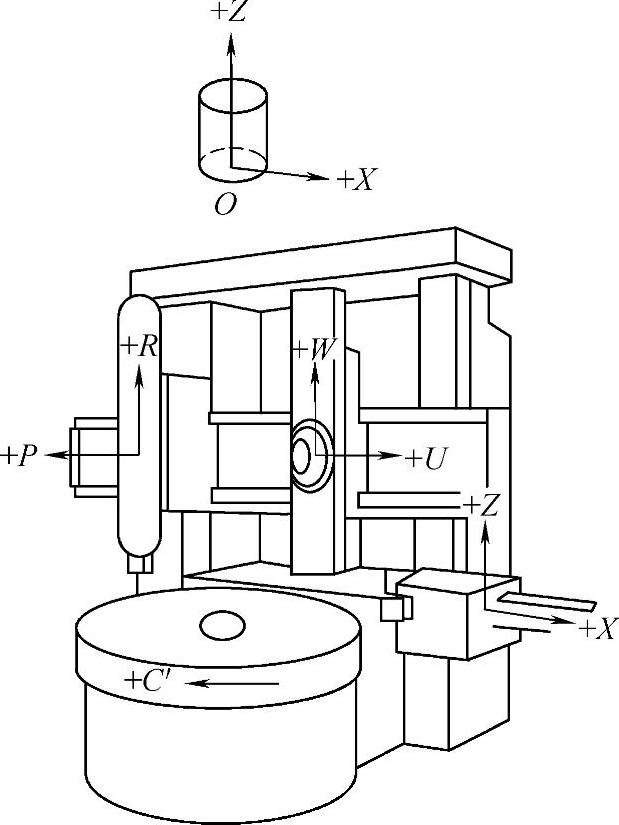
图2-14 数控双柱立式车床

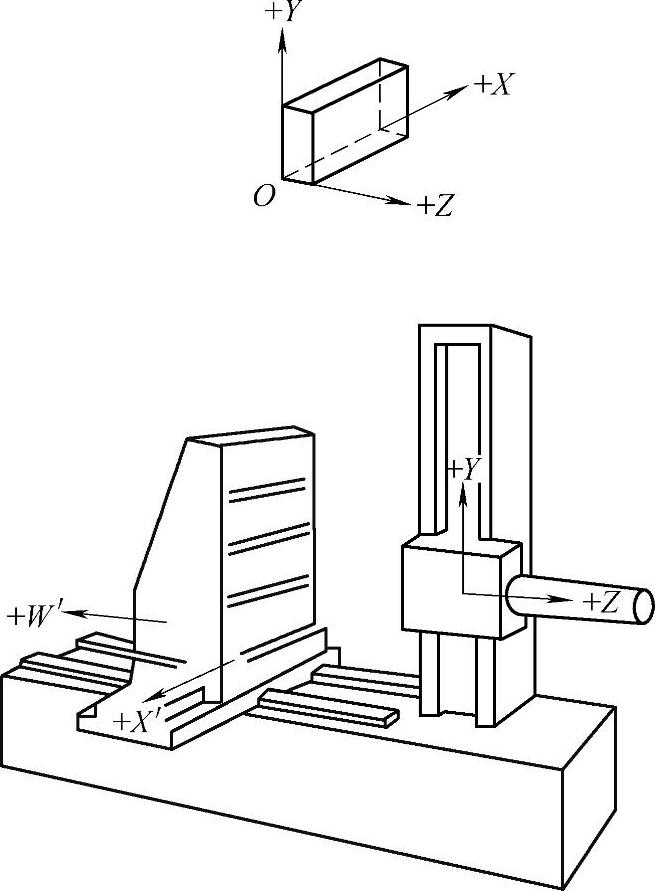
图2-15 数控卧式铣镗床

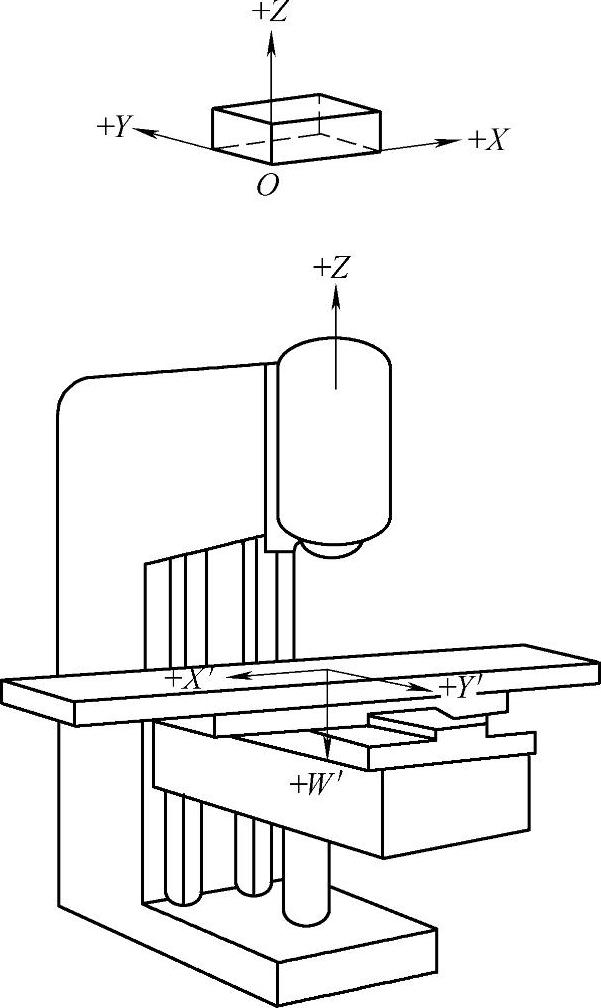
图2-16 数控立式升降台铣床

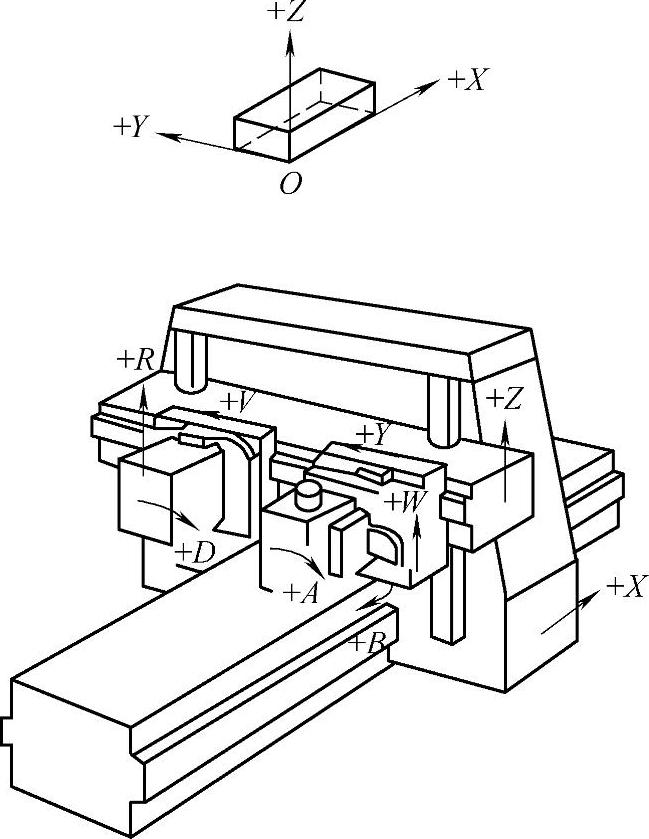
图2-17 龙门移动式数控铣床

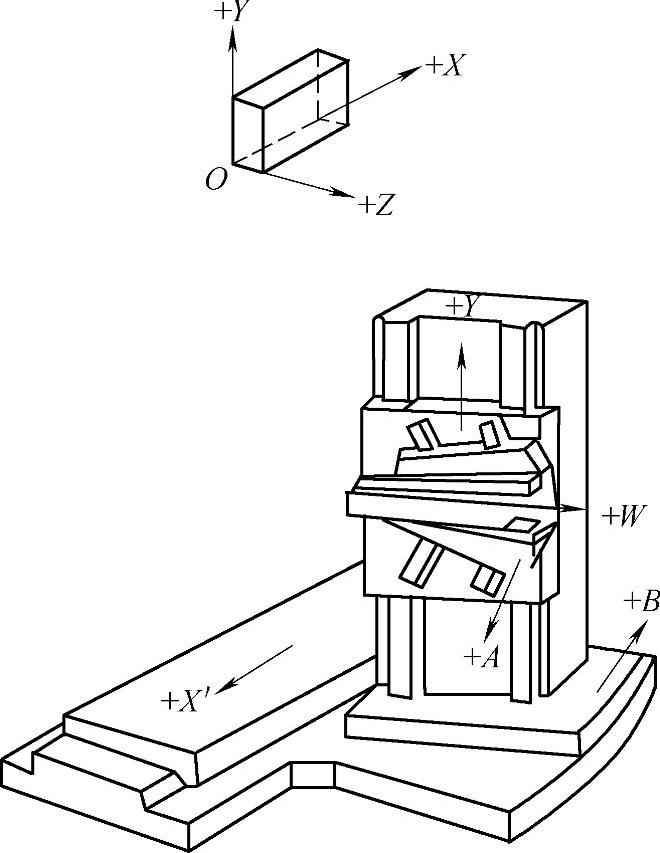
图2-18 五坐标工作台移动式数控铣床

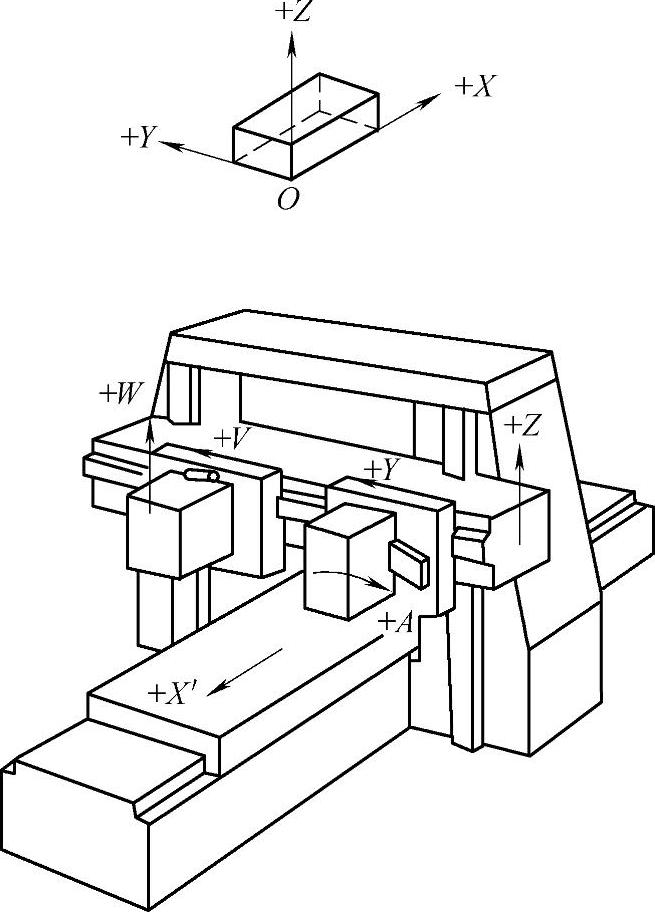
图2-19 数控龙门铣床

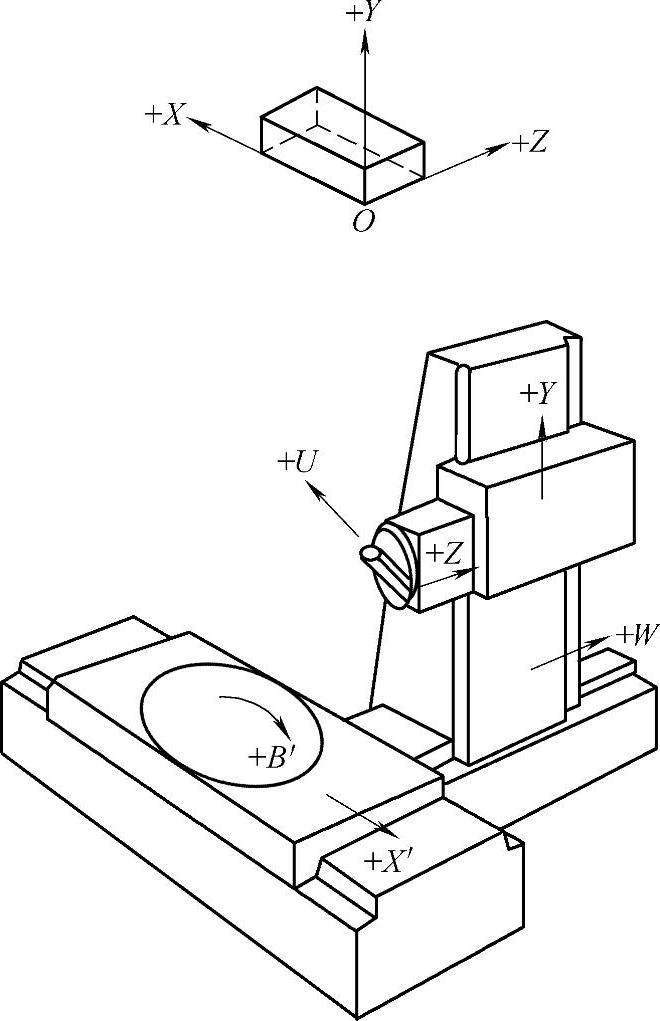
图2-20 数控卧式镗铣床

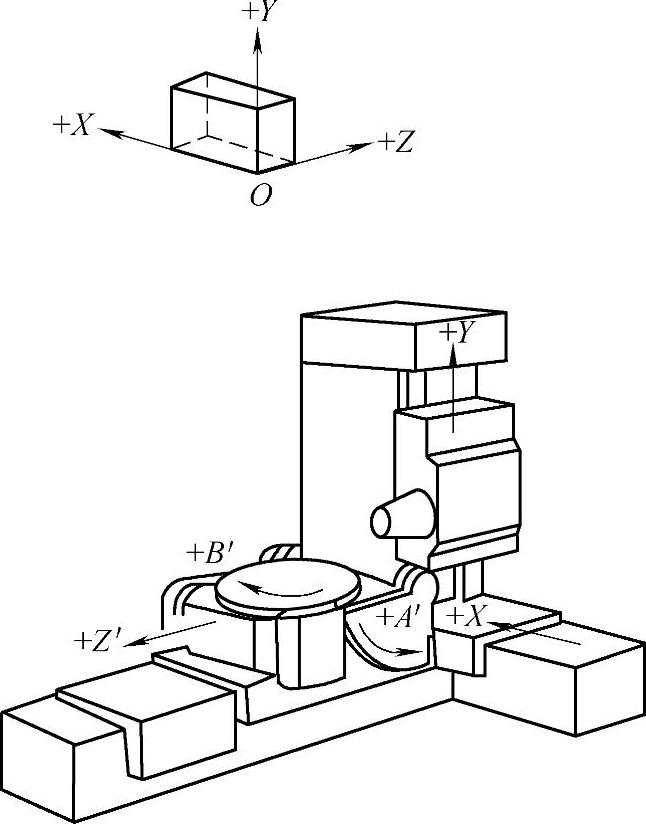
图2-21 五坐标摆动工作台数控铣床

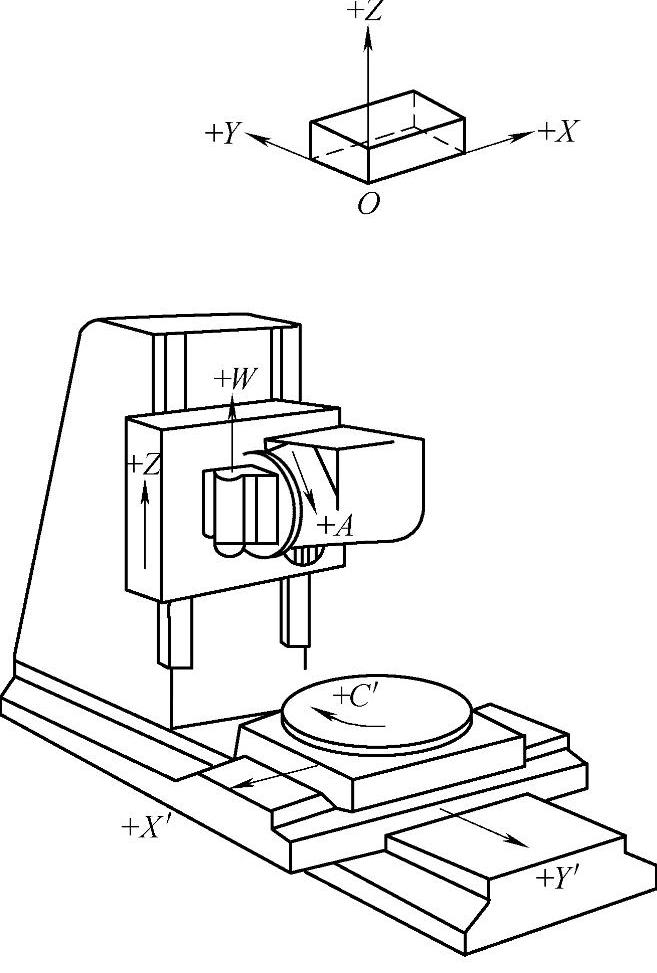
图2-22 五坐标摆动铣头式数控铣床

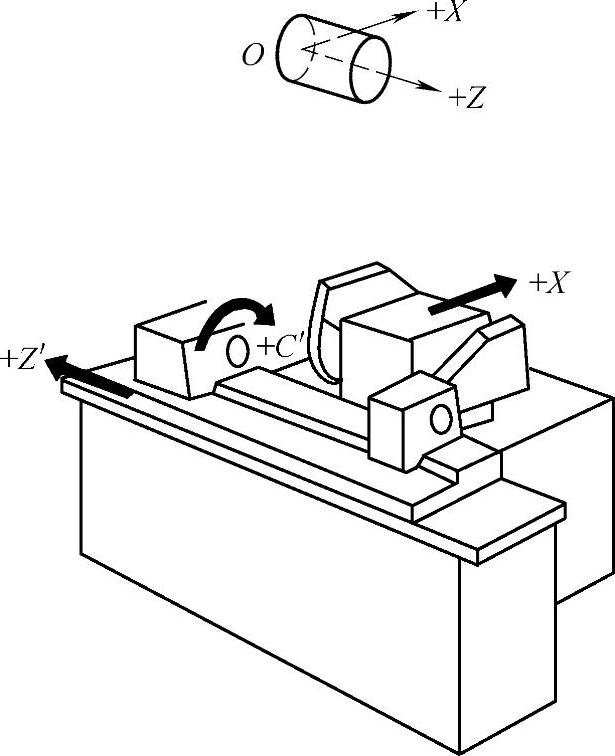
图2-23 数控外圆磨床

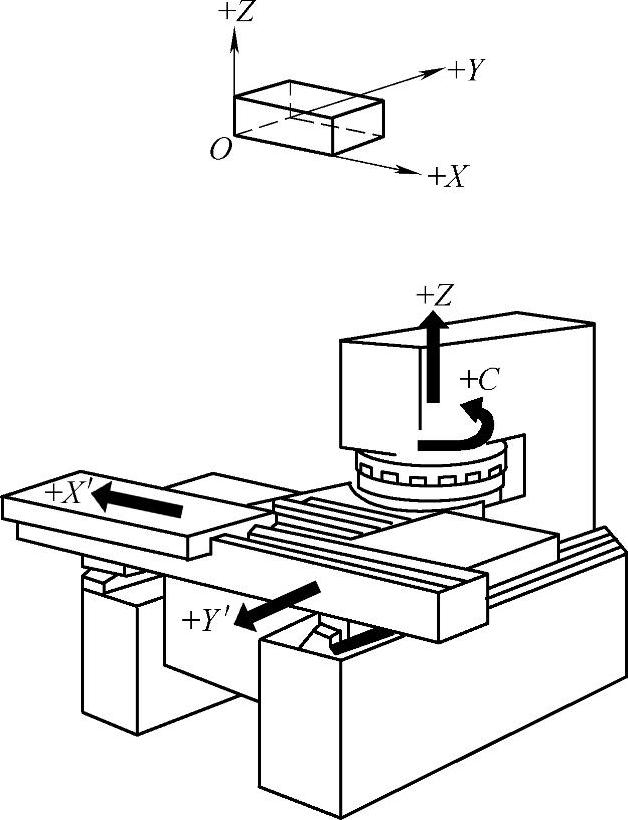
图2-24 数控转盘式冲床

2.坐标系原点

在确定坐标轴与运动方向之后，还需要进一步了解坐标系原点。

（1）机床原点

机床坐标系是机床固有的坐标系，机床坐标系的原点称为机床原点或机床零点，在机床经过设计、制造和调整后，这个原点便被确定下来，它是一个固定的点。在数控车床上，机床原点一般取在卡盘端面与主轴中心线的交点处。在数控铣床上，机床原点一般取在X，Y，Z坐标的正方向极限位置上，如图2-25所示。

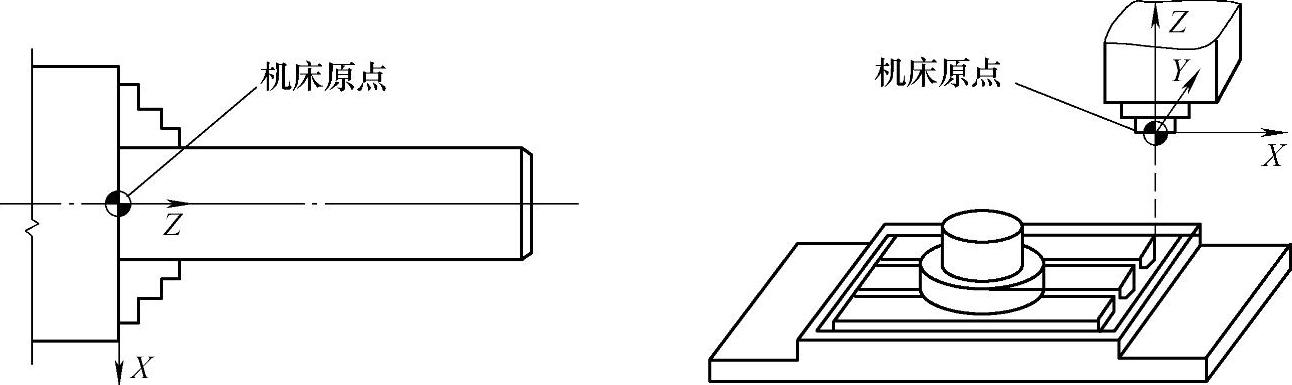
图2-25 数控车床、数控铣床的机床原点

（2）机床参考点

数控系统上电时并不知道机床原点在哪里。为了工作时正确地建立机床坐标系，通常在每个坐标轴的移动范围内设置一个机床参考点。机床参考点的位置是由机床制造厂家在每个进给轴上用限位开关精确调整好的。(www.xing528.com)

机床起动时，通常要进行参考点操作，建立机床坐标系；机床参考点可以与机床原点重合，也可以不重合，但参考点对机床原点的坐标必须是一个已知数。通过参数指定机床参考点到机床原点的距离，当机床回到参考点位置时，数控系统就知道了机床坐标系原点的位置。图2-26描述了数控车床参考点与机床原点的关系。

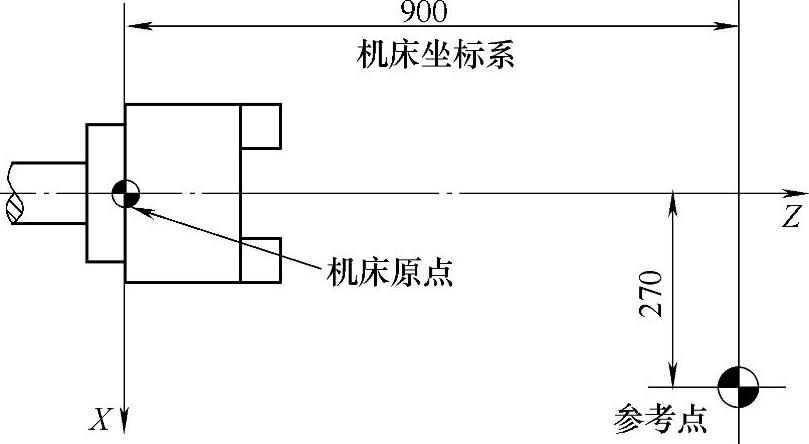
图2-26 数控车床参考点与机床原点的关系

3.工件坐标系

工件坐标系是编程人员在编程时使用的，由编程人员选择工件上的某一已知点为原点（也称程序原点）建立一个坐标系。确定工件坐标系时不必考虑工件毛坯在机床上的实际装夹位置，但工件坐标系中各轴的方向应该与所使用的数控机床相应的坐标轴方向一致。

工件坐标系原点的选择要尽量满足编程简单、尺寸换算少、引起的加工误差小等要求。一般情况下，在数控车床上加工的零件，编程人员往往将编程原点设在工件的右端面中心点上；在立式数控铣床上加工零件时，编程人员往往将Z₀设在工件的上表面，X₀、Y₀设在与零件的设计基准重合的地方，这样有利于在程序校验时借助判断坐标的正、负值，识别刀具当前所处的位置是离开了工件还是嵌入工件的实体内，同时减少了尺寸换算误差，使基点坐标容易计算。

4.编程尺寸的取值方法

零件图上标注几何点坐标位置的方法一般有两大类：绝对坐标取值和增量坐标取值。

绝对坐标取值是指零件以工件坐标系原点为基准给出的坐标值。

增量坐标取值是指零件上后一点的坐标相对于前一点的增量值。

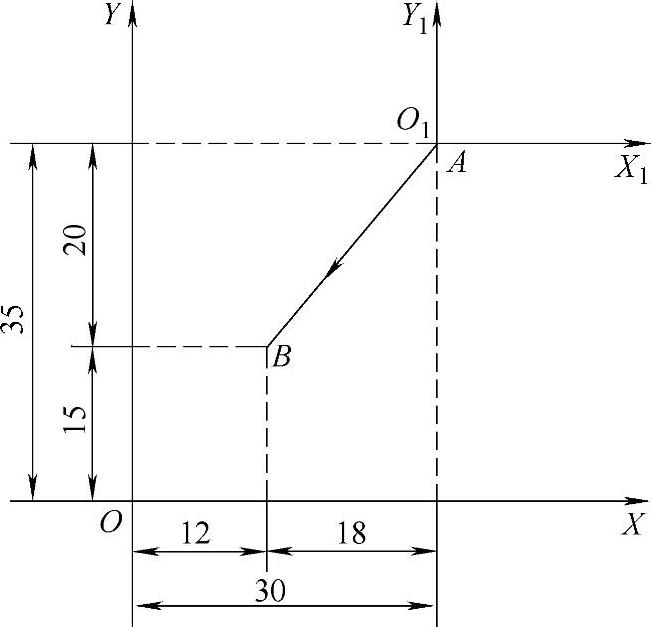
图2-27 绝对坐标与增量坐标

图2-27中，表示A→B运动方向的坐标，若以绝对坐标标记，O为工件坐标系原点，A点的坐标为（30，35）；B点的坐标为（12，15）。

若以增量坐标标记，图中A为刀具当前点，到B点的坐标值应表示为（-18，-20），其中负号表示B点相对于A点在X₁，Y₁轴的负向。

5.程序编制中的数值计算

根据零件图样，按照已确定的加工路线和允许的编程误差，计算出程序编制中所需要的各种基点或节点的坐标数值，这就是所谓的数值计算。零件程序编制过程中，除了点位加工这种简单的情况外，一般需经过繁琐、复杂的数值计算。为了提高工效，降低出错率，有效的途径是利用计算机辅助完成坐标数据的计算或直接采用自动编程。

（1）基点坐标的计算

数控机床一般只配置有直线和圆弧插补功能，因此，对于由直线和圆弧组成的轮廓编程时数值计算的主要任务是求各基点的坐标。

构成零件轮廓的不同几何直线的交点或切点称为总点。如直线与直线的交点、直线与圆弧的交点或切点、圆弧与圆弧的交点或切点等，基点可以直接作为运动轨迹的起点或终点。图2-28中的A，B，C，D，E，F，各点都是该零件轮廓上的基点。

基点坐标计算的主要内容有，每条运动轨迹（线段）的起点或终点、在选定坐标系中的坐标值、圆弧运动轨迹的圆心坐标值等。

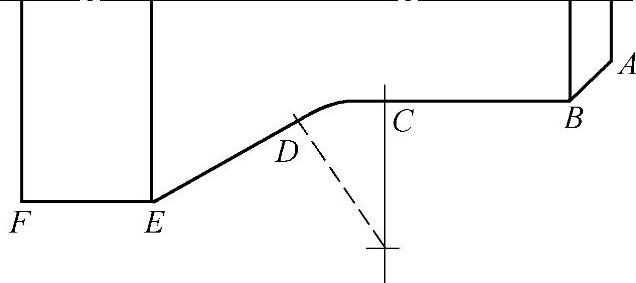
图2-28 零件轮廓上的基点

基点坐标计算的方法比较简单，一般可根据零件图样所给已知条件由人工计算完成。即根据零件图样给定的尺寸，运用代数、三角函数、几何或解析几何的有关知识，直接计算出数值。

常用的计算公式有：

勾股定理a²=b²+c²

余弦定理c²=a²+b²-2ab·cosα

三角函数sinα=y/r

cosα=x/r

tanα=y/x

直线方程常用形式有：

1）已知直线上一点（x₀，y₀）以及直线斜率k，则直线方程为y-y₀=k（x-x₀）

2）已知直线上两点（x₁，y₁），（x₂，y₂），则直线方程为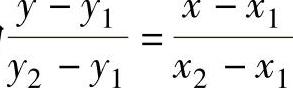

3）已知直线的斜率k以及在Y轴上的截距b，则直线方程为y=kx+b

已知圆心坐标为（x₀，y₀），半径为r，则圆方程为（x-x₀）²+（y-y₀）²=r²

【例2-1】如图2-29中，基点A，B，D，E的坐标值，从图中给出的尺寸可以很容易地得到，如A（0，0），B（0，12），D（110，26），E（110，0）。但基点C是过B点的直线与圆心为O₁，半径为30的圆弧的切点，这个尺寸，图中并未直接给出，要用解联立方程组的方法，才能求出切点C的坐标。

解：求C点的坐标值有多种方法，这里采用直线方程与圆方程联立求解的方法。先求出直线BC的方程，然后与圆心为O₁、半径为30的圆的方程联立求解。为方便求解，可以将坐标原点移到B点上。

依据已知条件列出BC直线方程：

y=tan（α+β）·x

圆弧方程：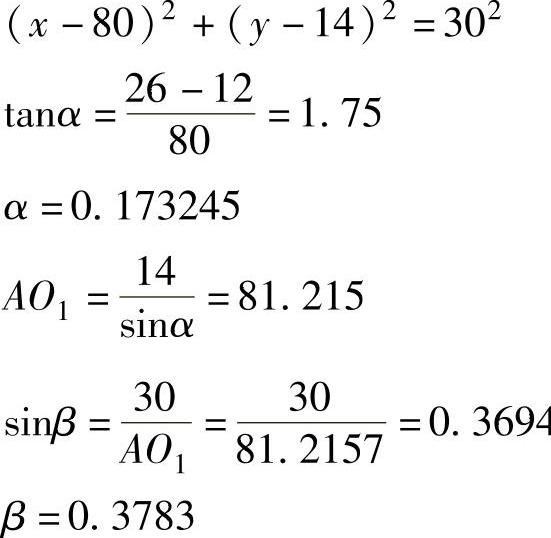

解直线方程与圆弧方程，可求得以B为原点的C点坐标为（64.2786，39.5507），换算到以A点为原点的编程坐标系中，C点坐标为（64.2786，51.5507）。

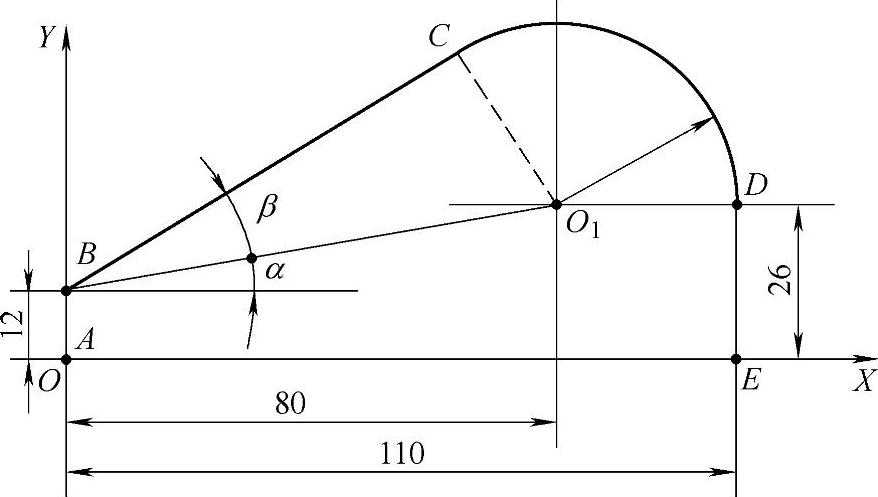
图2-29 基点坐标的计算

可以看出，如此简单的零件，基点的计算都很麻烦，对于复杂的零件，其计算工作量可想而知。为提高编程效率，可应用CAD/CAM软件辅助编程。

（2）节点坐标的计算

有些平面轮廓是用非圆曲线方程y=f（x）表示的，如渐开线、阿基米德螺线、双曲线、抛物线等。还有一些平面轮廓是由一系列实验或经验数据点表示的，没有表达平面轮廓形状的曲线方程，这类曲线常称为列表曲线。目前，国内使用的数控机床大多数不具备这些曲线的插补功能。对于具有非圆曲线的零件的插补运算，必须采用一般数控系统均具有的直线或圆弧插补功能去逼近完成，即将非圆轮廓曲线按编程允许误差分割成许多小段，再用直线或圆弧来代替（逼近）这些曲线小段，使这些直线或圆弧与被逼近的曲线每小段的误差不小于编程误差。用若干直线段或圆弧来拟合（逼近）非圆曲线，拟合线段的结点或切点称为节点。

通常，计算非圆曲线的节点坐标是借助于计算机来完成的。其基本计算过程可按下列步骤进行：

1）选择插补方式：即选择直线插补还是圆弧插补来逼近非圆曲线。

2）确定编程允差值：要求编程的误差值小于零件允许的误差值。

3）确定计算方法：非圆曲线节点计算过程一般较复杂，实际应用中的算法也很多。选用什么方法，主要考虑依据是要在能满足编程允差的条件下，使程序段少些，同时应尽可能使算法简单，容易实现。

4）绘制计算机算法流程框图。

5）根据流程框图编写运算程序。

6）上机调试程序，算出节点坐标值。

常用的直线逼近非圆曲线的节点计算方法有等间距法、等步长法和等误差法等。

常用圆弧逼近非圆曲线的节点计算方法有曲率圆法、三点圆法、双圆弧法和相切圆法。

通常圆弧逼近比直线逼近的曲线要光滑一些，但计算较复杂。因此，一般情况下直线逼近的方法应用较广泛，如应用CAM软件自动编程中的节点大部分都是采用直线逼近法计算节点坐标。

列表曲线的已知点就是节点，如果已知点足够多，只要直接将已知点输入进行编程，就可得到相对应的轮廓。但出于已知点的密度不够多，会使插补所得曲线不够光滑，因此常常需要对列表点进行数学处理。常用的方法有三次样条曲线拟合法、牛顿插值法、圆弧样条拟合法和双圆弧样条拟合法等。

在列表收线的数学处理过程中，通常要注意下列两个方面的问题：

1）拟合的曲线方程表达式必须通过已知列表点。

2）列表点间要求尽可能光滑过渡，尽量减少新的拐点出现。