对接接头应力集中系数的优化解决方案

对接焊接接头应力集中的因素影响有很多，包括焊趾倾角θ、焊趾过渡圆弧半径r、板厚t、余高 h、焊缝宽度W 等诸多因素[23]，由于焊接接头的疲劳断裂总是发生在对接接头的焊趾处，因此分析应力集中系数主要是考虑焊趾处应力分布情况。文献[24-27]曾就几何参数对焊接接头的应力集中系数的影响开展过一些研究。文献[28-29]利用软件建立有限元模型并计算，分别分析了16MnR、P355NL1 钢焊接接头的应力集中系数。由于应力集中系数主要取决于试样的形状，因此其计算结果对于其他材料都有一定参考意义。

文献[30]计算时所用的MB8 镁合金对接接头试样的形状、尺寸及实物图如图5-10 所示。

图5-10　MB8 对接接头的形状、尺寸及实物图

由于模型的对称性，故取其1/8 进行分析。有限元网格模型及网格划分如图5-11 所示。为了分析较大圆弧过渡处的应力集中，采用了相应的网格细化。

计算时焊缝宽度W=6 mm，应力集中系数Kt随焊趾倾角θ、焊趾过渡圆弧半径r 两个因素的变化情况。为了考查焊趾倾角θ 和焊趾过渡圆弧半径r对应力集中系数的影响，焊趾倾角θ 从10°变化到60°，焊趾过渡圆弧半径r从0.2 mm 变化到8 mm，焊趾处的应力集中系数用焊趾处最大的应力与所在截面的平均应力之比。计算结果如表5-1 和图5-12 所示。

图5-11　MB8 对接接头试样模型有限元网格

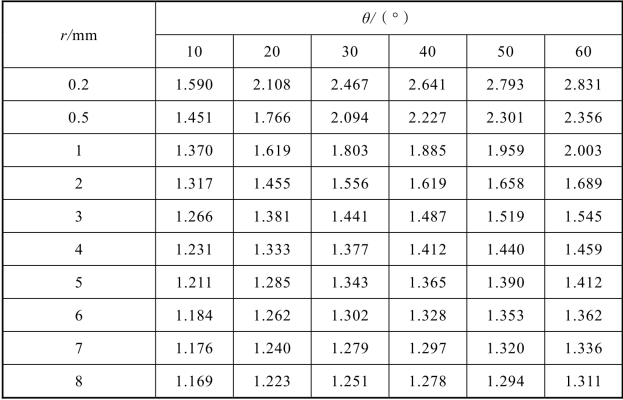
表5-1　MB8 对接应力集中系数Kt随r 与θ 变化（w=6mm）

(www.xing528.com)

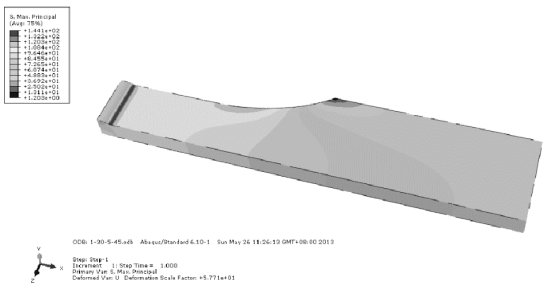
图5-12　MB8 对接接头第一主应力云图

在MB8 镁合金母材试样的疲劳试验中，镁合金母材全部在圆弧的过渡区发生断裂，如图5-13 所示。这是因为在圆弧过渡区域的应力集中情况比较严重，在加载的过程中，该区域受到的力要比其他区域受到的力大很多，所以该区域会率先萌生裂纹并扩展至断裂。从图5-12 中可以看出MB8 镁合金焊接接头的应力集中在焊趾处是比较大的。在焊接接头的疲劳试验中，接头断裂位置也充分证明了计算结果的正确性，如图5-14 所示。

图5-13　MB8 镁合金母材断于圆弧过渡区

图5-14　MB8 镁合金焊接接头疲劳裂纹起源于焊址处

从表5-1 中可以看出，焊趾圆弧过渡半径r 对MB8 镁合金焊接接头应力集中系数的大小有着很大的影响。对于相同的焊趾倾角，随着过渡圆弧半径r的不断增大，应力集中系数逐渐减小。当过渡半径r 在较小的数值区变化时，其对于应力集中的减小是非常有效的，应力集中系数下降较快；当r 在较大数值区变化时，虽然也可以降低应力集中，但是相对于r 在较小数值区来说降低较少。例如，当焊趾倾角θ=30°时，焊趾圆弧过渡半径r 从0.2 mm 增加到3 mm 时，应力集中系数Kt从2.467 下降到1.441，降幅为41.58%；焊趾圆弧过渡半径r 从3 mm 增加到8 mm 时，应力集中系数Kt从1.441 下降到1.251，降幅仅为11.19%。

从表5-1 中还可看出，焊趾倾角θ 对焊接接头应力集中系数的大小也有着很大的影响。对于不同的过渡半径下的应力集中系数Kt是随着倾角θ 的不断增大而增大的。当过渡半径r=0.5 mm 时，θ 从10°增加到60°，应力集中系数Kt从1.451 增加到2.356，增幅为62.37%；当焊趾圆弧过渡半径r=8 mm 时，应力集中系数Kt从1.169 增加大1.311，增幅为12.15%。随着过渡半径的不断增大，倾角θ 对应力集中的影响在不断减小。