疲劳裂纹扩展速率优化策略

对上述的a-N 曲线，在双对数坐标上作图（lgda/dN-lgΔK），发现疲劳裂纹扩展可分为如下3 个区域，如图3-32 所示。

图3-32　疲劳裂纹扩展速率曲线

Ⅰ区为近门槛区，裂纹扩展速率随 ΔK 的降低而迅速降低，以至da/dN→0。与此相对应 ΔK 值称为疲劳裂纹扩展的门槛值，记为ΔKth，表示阻止裂纹扩展的能力；ΔKth越大，材料的抗疲劳性能越好。

当 ΔK ≤ΔKth时，da/dN=0，裂纹不扩展；当 ΔK ＞ΔKth时，da/dN＞0，裂纹开始扩展且扩展速度较快，很快进入第二个区域。

研究疲劳裂纹门槛值在理论上和实际工程应用上都是有意义的。ΔKth很小，约为KIC的5%～10%。所以，一般的机械零件和工程构件是不会以ΔKth来作为设计指标的，如以ΔKth来作为设计标准，这无疑是要求工作应力很低或者容许的裂纹尺寸很小，是不切合实际的。疲劳门槛值除了因应力比R 的增加而减小外，还和组织有关。Ⅰ区接近于ΔKth，故又将Ⅰ区称为近门槛区。其断口为解理花样，由断裂小面组成。

Ⅱ区为中部区或稳态扩展区，是裂纹扩展的主要阶段，决定了疲劳寿命的主要部分。其扩展速率受应力比、组织类型和环境的影响很小。

Ⅱ区的裂纹扩展速率da/dN=10-8～10-6m/周次。在Ⅱ区，帕瑞斯（Paris）公式较好符合该区域，裂纹扩展速率在lgda/dN-lg ΔK 双对数坐标上呈一直线关系。对钢材而言，屈服强度、抗拉强度、加工硬化特性、组织结构以及温度等对此阶段的斜率基本上不发生明显的影响。从试样断口可以看出，在此扩展阶段内为平断口，与外加拉应力成90o。电子金相图片表明为穿晶断裂，且具有典型的疲劳辉纹。

Ⅲ区为裂纹快速扩展区，da/dN＞（10-6～10-5）m/周次，并随着 ΔK 的增大而迅速升高。当Kmax= ΔK /(1-R)=σmax(πa)1/2=KIC时，试件或零件断裂。这一阶段受应力比、组织和断裂韧性的影响较大。其断口呈现静载断裂机制。

Paris 公式有两个缺点：

（1）它没有考虑平均应力对da/dN 的影响，而试验证明平均应力对疲劳裂纹扩展速率是有显著影响的；

（2）它没有考虑当裂纹尖端应力强度因子趋近于临界值KIC时，裂纹的加速扩展效应。

考虑上述两个存在的问题，福尔曼（Forman）提出了以下修正公式[21，22]：

式中， ΔK 为应力强度因子范围（ ΔK =Kmax-Kmin）；KIC为应力强度因子的临界值；C、n 均为由材料决定的常数；r 为应力比。

福尔曼（Forman）公式不仅考虑了平均应力对裂纹扩展速率的影响，而且反映了断裂韧度的影响。它可以在任何r 的条件下更好地描述疲劳裂纹扩展规律，同时表明da/dN 数值不仅取决于 ΔK 的大小，还与KIC有关，材料的KIC越大，da/dN 数值越小。

如图3-33 所示为7075-T6 铝合金在各种r 值条件下的帕瑞斯（Paris）公式表示的d a /d N- ΔK 的关系。可见同一个 ΔK 值下r 值越高（亦即平均应力越高），裂纹扩展速率也越高。同时亦可看到每条线都有自己单独的“指数规律”关系。但是，如果用福尔曼公式处理图中的5 组数据，则得到如图3-34 所示的一条线，其斜率为4。这说明修正公式有比帕瑞斯公式更好的概括性。(www.xing528.com)

虽然福尔曼公式在处理许多材料（特别是高强度钢、铝合金）的数据中，获得了广泛的应用，但由于此公式中有材料的KIC值，这就使得不能用它描述目前尚难以测定出KIC值的高韧性材料的裂纹扩展规律。因此，华格（Walker）提出用如下公式来描述裂纹扩展规律：

式中，m、n、C 为与材料和介质有关的常数。

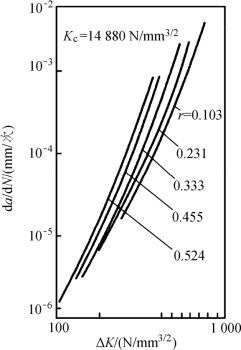
图3-33　按照Paris 公式绘制的d a /d N -ΔK 的关系

图3-34　按照Forman 公式绘制的da/dN[(1-r)KIC- ΔK ]与 ΔK 的关系

华格称Kmax(1 -r)m为有效应力强度因子。当m=1 时，则它与帕瑞斯（Paris）公式完全一致。可以说，帕瑞斯指数规律公式可看作是华格公式的特例。如图3-35 所示为图3-33 的5 组数据用华格公式处理的结果。

以上所讨论的是在应力循环条件下，裂纹在弹性区内的扩展规律。应当说明，这些规律的应用范围是低应力、高循环、低扩展速率。而这种指数规律不能用来表征高应变循环条件下裂纹的扩展规律。高应变循环疲劳也称为低循环疲劳或塑性疲劳。它一般发生在高应力、低循环、高扩展速率的情况下，此时试验条件不是控制应力，而是控制应变幅值。

断裂力学中用裂纹尖端的张开位移来描述此时的裂纹扩展规律，即

式中，Δδt为裂纹尖端的张开位移幅度。

图3-35 按照Walker 公式绘制的da/dN-ΔK 关系

试验结果表明，当张开位移幅度Δδt=常数时，则da/dN 变为一恒值。这就是说在控制裂纹张开位移幅度Δδt的条件下，裂纹张开位移幅度Δδt就是影响裂纹扩展速率的主要参量。不过到目前为止，有关这方面的试验做得尚不够多，需要继续进行研究。

多年以来，试图将断裂力学的理论用于焊接结构的疲劳强度评估的努力一直没有停止过，像BSI 2015 标准《钢结构抗疲劳设计与评估》那样，对如何使用断裂力学进行疲劳评估也提供了指导[23]。然而，它又特别提醒在使用断裂力学进行疲劳评估时需要格外小心，例如在裂纹扩展方程中的取值，初始缺陷的尺寸和疲劳裂纹的形状，甚至对于焊趾上的裂纹，它是半椭圆形的还是直线形的，都需要事先做出假设，而这些假设在设计阶段通常是难以建立的。即使这些假设可以被建立，它也完全有可能因人而异，这样计算结果的唯一性就很难从理论上得到保证[24]。因此如何选用公式中的常量，或者说公式中的常量选取正确与否对计算结果的准确性影响是至关重要的。