优化生产力：考虑输出力

执行机构不论是哪种类型，它的输出力都是用于克服负荷的有效力。而负荷主要是指不平衡力和不平衡力矩加摩擦力、密封力、重力等有关的作用力。

为了使调节阀能正常工作，选配的执行机构要能产生足够的输出力来克服各种阻力，保证严格的密封或阀门的开启。

对双作用的气动、电-液、电动执行机构，一般都没有复位弹簧，作用力的大小与它的运动方向无关，因此选择执行机构的关键在于了解最大输出力或电动机的转动力矩。

对于单作用气动执行机构，输出力与控制阀开度有关，调节阀上出现的力也将影响运动特性，因此要求在整个调节阀的开度范围建立力平衡。如果执行机构的输出力为F，它的力平衡方程式为

F=F_P+F_M+F_T+F_W （8-34）

式中，F_P为作用在阀芯上流体不平衡力（N）；F_M为调节阀关闭时阀芯对阀座的密封力（N）；F_T为阀杆与填料间的摩擦力（N）；F_W为阀芯和各种活动部件的重力（N）。

当采用波纹管阀杆密封调节阀时，还应该考虑波纹管随调节阀开度而变的阻力。式（8-34）中各种力的大小和方向随执行机构的类型而变化，下面将讨论典型的执行机构。

1.气动薄膜执行机构的输出力

带弹簧的气动膜片执行机构，由于膜片室信号压力所产生的推力大部分被弹簧力所平衡，因此有效输出力比无弹簧型要小。

根据调节阀不平衡力的方向性，执行机构输出力有相应的两种不同方向。设+F表示执行机构向下的推力，-F表示执行机构向上的输出力，如图8-3所示。

无论是正作用式或反作用式的气动膜片执行机构，它们的正向或反向输出力±F均为信号压力p作用在膜片有效面积A_e上的推力pA_e与弹簧的反作用力C_s（L₀+l）之差，即

±F=pA_e-C_s（L₀+l） （8-35）

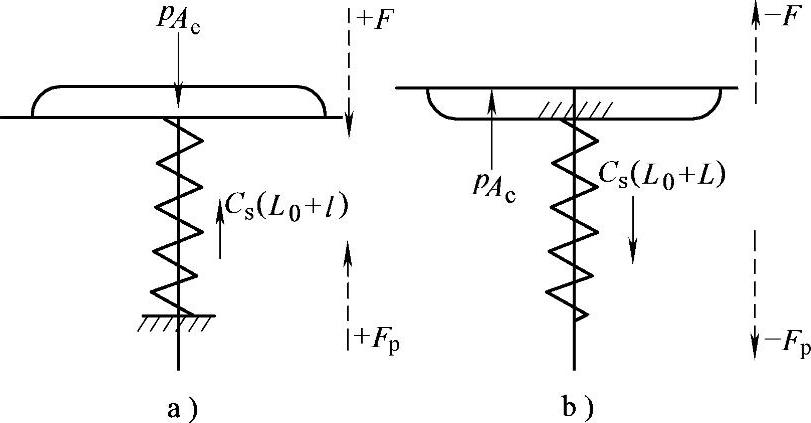
图8-3 膜片式执行机构输出力

a）正作用式 b）反作用式

式中，A_e为膜片有效面积（m²）；l为推杆位移量（m）；C_s为弹簧刚度（N/m）。

p_r为弹簧范围，相当于使弹簧产生全行程变形量L所需加在膜片上的压力变化范围（Pa）；L₀为弹簧预紧量（m）。

p_i为弹簧的启动压力，相当于使弹簧产生预紧变形量L₀所需加在膜片上的压力。弹簧在自由状态时，p_i=0，p_i可根据需要在一定范围内调节。将式（8-36）、式（8-37）代入式（8-35）可得

式（8-38）中的p_F为有效的输出压力，是用来克服负荷的有效压力。增大p_F或增大有效面积A_e，都可以提高执行机构的输力F。

目前，调节阀使用的弹簧范围有20～60kPa、20～100kPa，40～200kPa、60～100kPa、60～180kPa等多种，分别调整各种弹簧的启动压力，可使执行机构具有不同的输出力。不同的弹簧范围与不同有效面积的膜片相匹配之后，可得到不同的输出力，见表8-17、表8-22中所给出的输出力为近似值。

表8-17 气动膜片执行机构的输出力 （单位：N）

2.活塞式执行机构的输出力

常见的活塞式执行机构有单向和双向两种作用方式。双向活塞执行机构在结构上是没有弹簧的。由于没有弹簧反作用力，它的输出力比膜片式执行机构大，常用作公称尺寸DN较大、高压差调节阀的执行机构。

图8-4所示为双向活塞执行机构的受力情况。

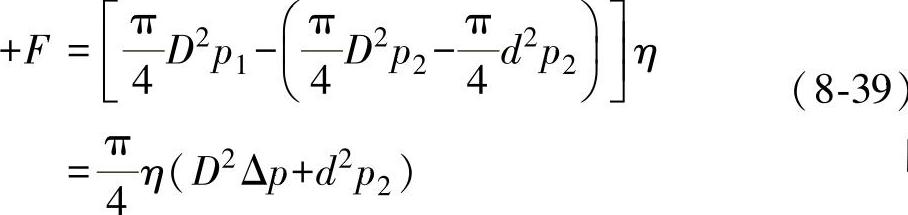
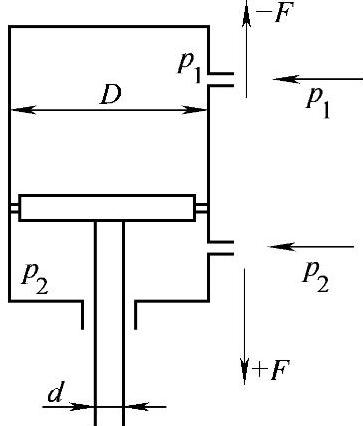
图8-4 活塞执行机构的输出力

式中，F为执行机构输出力（N）；D为活塞直径（mm）；d为活塞杆直径（mm）；p₁、p₂为上、下缸工作压力（MPa）；Δp为压差（MPa）；η为活塞缸效率，考虑到摩擦消耗，取η=0.9。

因为活塞杆处于极端位置时，p₂=0、p₁=p₀，p₀为最大工作压力，即阀门定位器的气源压力，因此有

当活塞向上动作时，输出力为-F，即

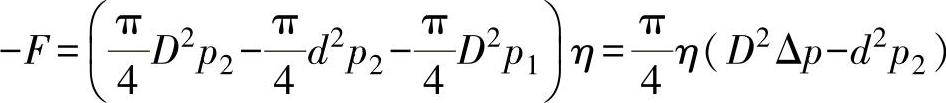
同样，当活塞杆处于另一极端位置时，p₁=0、p₂=p₀，即

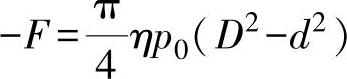
又由于活塞的直径比活塞杆直径大很多，因此有

综上可知，活塞执行机构输出力可用式（8-42）表示(www.xing528.com)

式（8-42）说明，活塞执行机构的输出力与活塞直径D，最大工作压力p₀和活塞缸效率η有关，一般p₀和η都一定（p₀=0.5～0.6MPa，η=0.9），因此输出力的大小主要决定于活塞的直径（表8-18）。

表8-18 活塞执行机构的输出力

3.不平衡力和不平衡力矩

流体通过调节阀时，阀芯受到静压和动压的作用，产生使阀芯上、下移动的轴向力和阀芯旋转的切向力。对于直线位移的调节阀来说，轴向力直接影响阀芯位移与执行机构信号力的关系，因此阀芯所受到的轴向合力称为不平衡力。对于角位移的调节阀，如球阀、蝶阀、偏心旋转阀等，影响其角位移的是关闭件的轴受到的切向合力矩，称之不平衡力矩。

影响不平衡力和不平衡力矩的因素很多，如控制阀的结构形式、公称尺寸DN（NPS）、流体的物理状态等。如果工艺流体及调节阀结构形式都已确定，不平衡力或不平衡力矩主要与阀前后的压差有关，也与流体与阀芯的相对流向有关。

流体流向不同时，阀芯所受到的不平衡力并不一样，图8-5所示为单座阀正装阀芯在两种不同流向下，压差不变时不平衡力与行程之间的关系曲线，图中假定使阀杆受压的不平衡力为“+”，使阀杆受拉伸的不平衡力为“-”；上面一种在流体流动时使阀芯打开，称为流开状态；下面一种在流体流动时使阀芯关闭，称为流闭状态。

图8-5所示的曲线表明，阀芯在全关位置时不平衡力F_p最大，随着阀芯开启而逐渐变小。由于中间位置动压难以用公式表示，因此在选择执行机构计算作用力时，主要根据全关时来确定。

对于流开状态，即阀杆在流体流出端时不平衡力F_P为

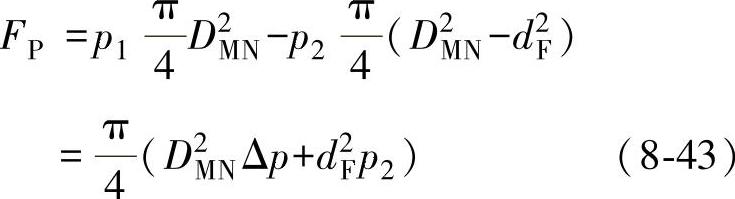
式中，D_MN为阀座内径（mm）；d_F为阀杆直径（mm）；p₁为阀前压力（MPa）；p₂为阀后压力（MPa）；Δp为压差（MPa），Δp=p₁-p₂。

从式（8-43）可以看出，F_P始终为正值，阀杆处于受压状态。另外，若D_MN、Δp和p₂越大，则不平衡力F_P越大。因此，对于高压差、公称尺寸DN（NPS）大的单座阀，不平衡力是较大的。

对于流闭状态（高进低出），即阀杆在流体流入端的不平衡力为

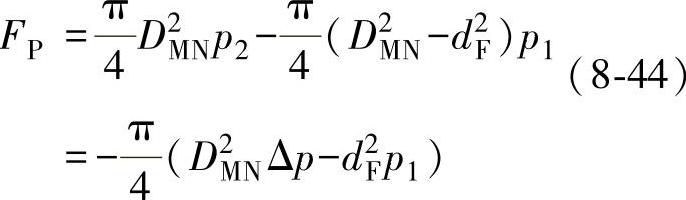
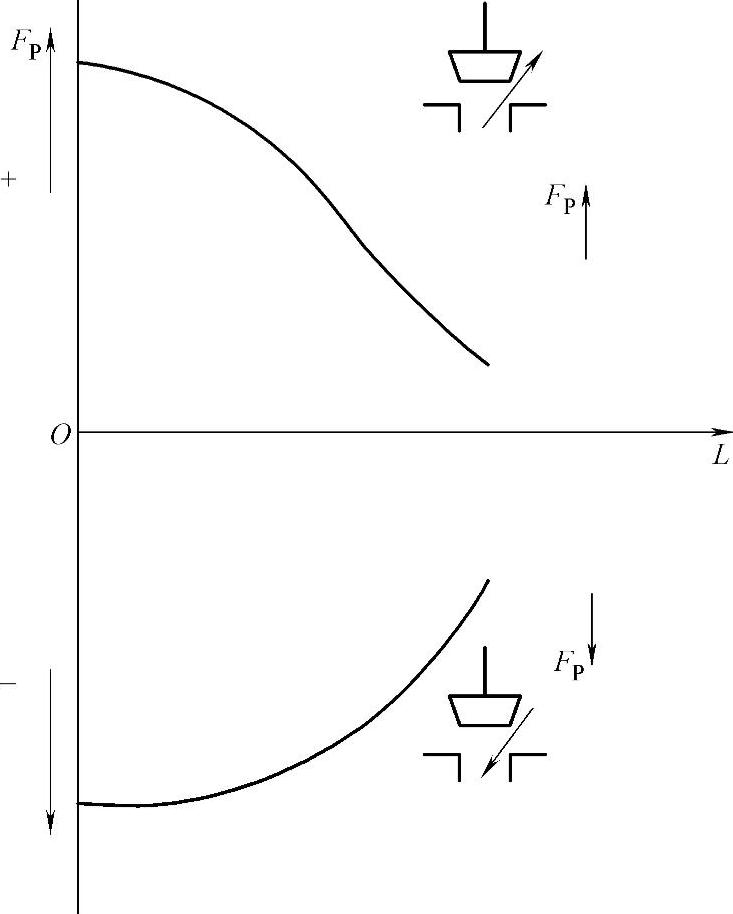
图8-5 单阀座不平衡力与流体流向的关系

从式（8-44）可以看出：对小流量阀及公称尺寸DN（NPS）小的高压阀，由于d_F≥D_MN，故FP为正值，阀杆受压；对于DN15以上的单座阀，因D_MN>>d_F，F_P为负值，因此阀杆受拉；阀的公称尺寸在此两者之间，即D_MN>d_F时，F_p可能为正，也可能为负，说明对同一台调节阀，在全行程范围内，有时由于p₁和p₂的变化，可能使阀杆所受的不平衡力发生方向的变化。

对于双座阀、三通阀、隔膜阀等类型，都可按上面介绍的方法计算不平衡力。对球阀、蝶阀、偏心旋转阀的不平衡力矩也有其计算公式，常见的计算公式见表8-19。

4.允许压差的计算

从前面计算公式可以看出，调节阀两端的压差Δp增大时，其不平衡力或不平衡力矩也随之增大，当执行机构的输出力小于不平衡力时，它就不能在全行程范围内实现输入信号和阀芯位移的准确关系。由于对确定的执行机构，其最大输出力是固定的，故调节阀应限制在一定的压差范围内工作，这个压差范围就称为允许压差，用[Δp]表示。

调节阀一般均使用流开状态，所以允许压差也就是指阀门处于流开状态时的允许压差，制造厂所列的允许压差一般均为p₂=0的数据，选用时需要注意。

执行机构的输出力F用于克服不平衡力、密封力、摩擦力和各种活动部件的重力。在正常润滑的情况下，摩擦力F_f很小，各种活动部件的重力也不大，因此在计算执行机构输出力时，一般可以把式（8-34）简化为

F=F_P+F_M （8-45）

也就是说，执行机构的输出力只能用来克服不平衡力F_P和阀门全闭时的密封力F_M，必须注意的是，调节阀摩擦力的大小，要看阀门结构、填料的材质、调节阀工作压力的大小来决定可否忽略，对一些公称尺寸DN（NPS）较大的阀门，如DN200笼式阀，其摩擦力高达1000N以上，就不能不予以考虑。

阀座密封力F_M的大小，决定于阀芯与阀座是金属密封还是非金属密封。对于金属密封的调节阀，F_M一般相当于p₀=0.5MPa乘以膜片的有效面积A_e的力，然后把已确定的执行机构输出力F及各种具体结构和使用情况的调节阀的不平衡力F_P的计算公式代入，便能得到允许压差[Δp]的计算公式。

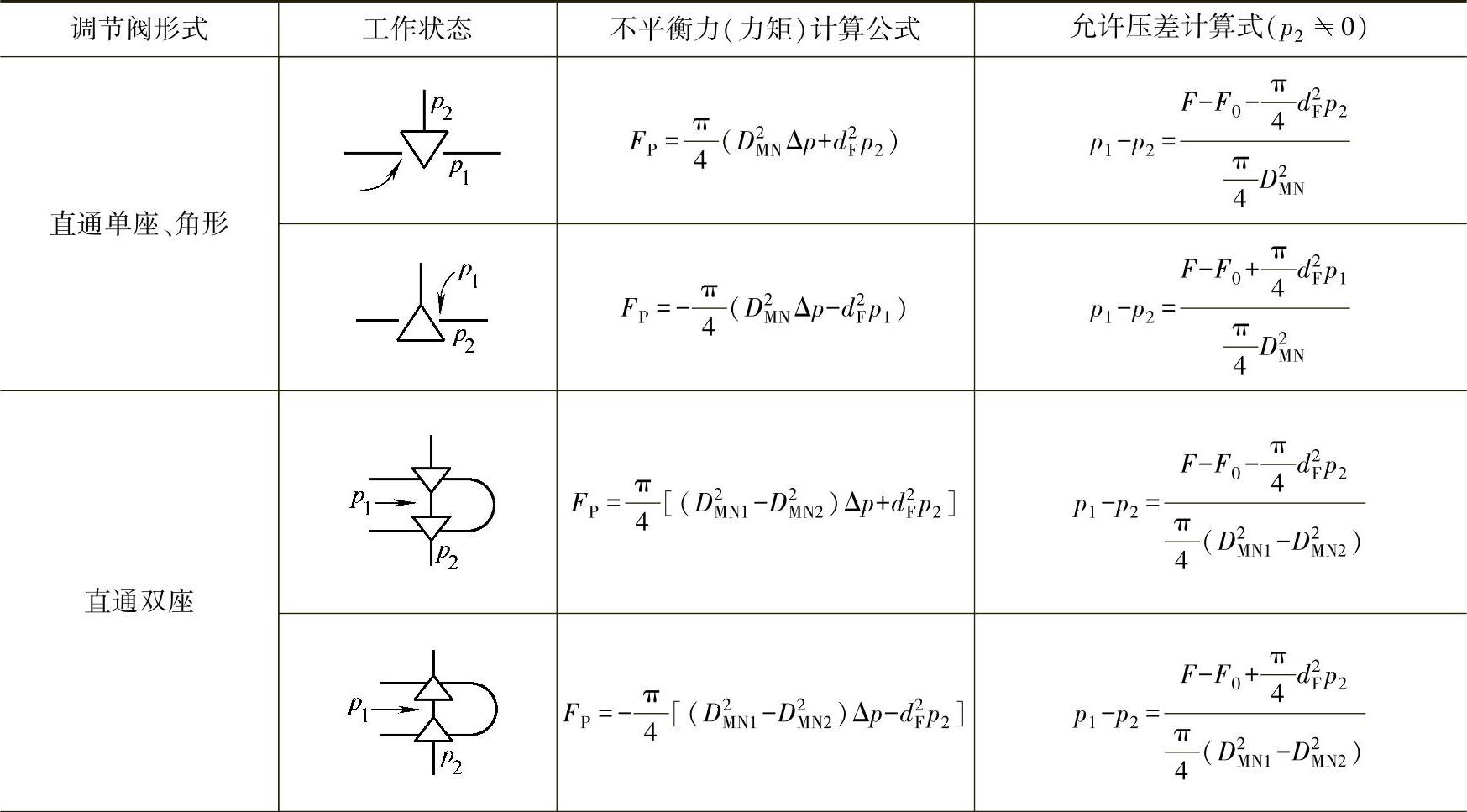
表8-19 各种调节阀的不平衡力和允许压差计算公式

（续）

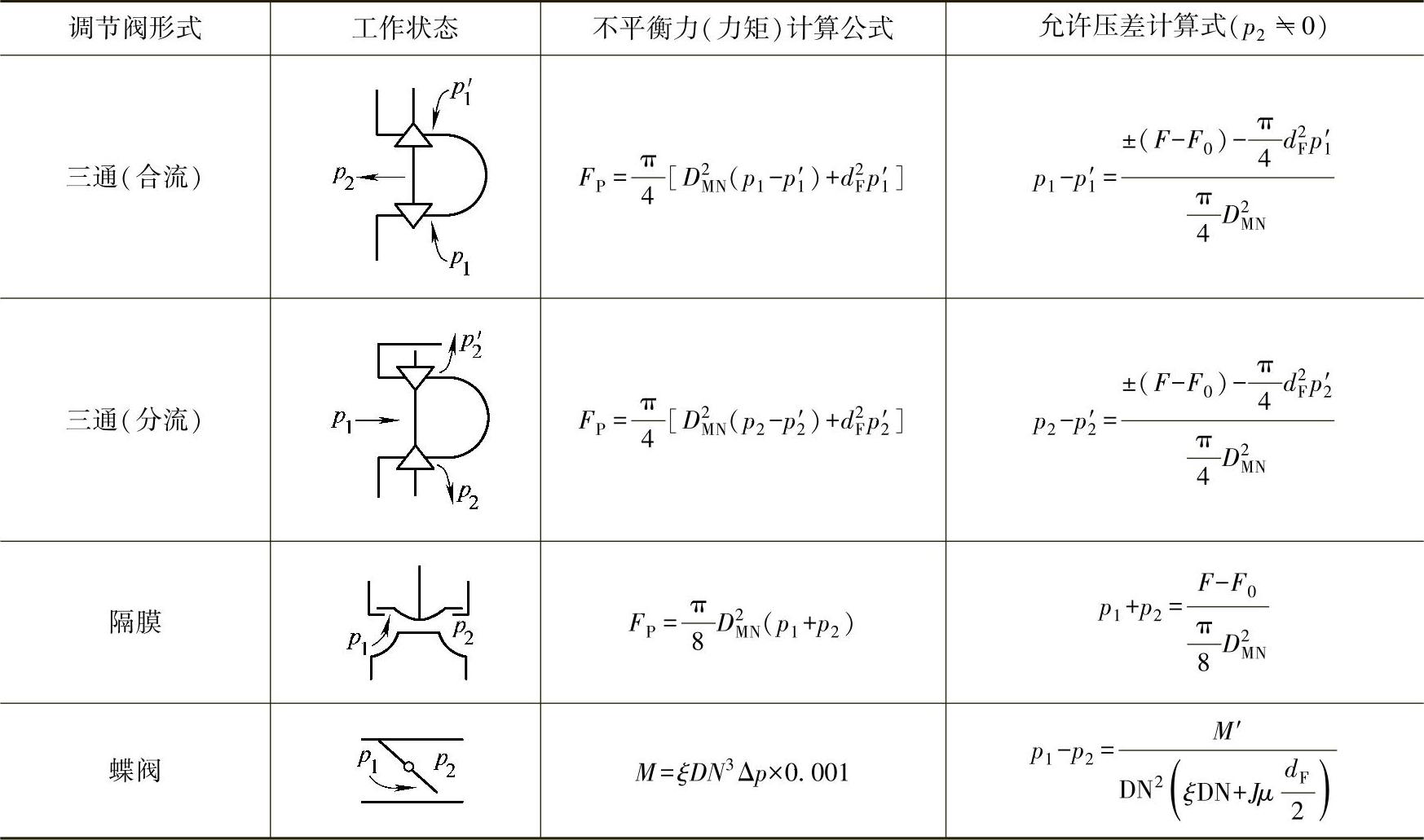
注：D_MN为阀座内径（mm）；F为执行机构的输出力（N）；ξ为蝶阀的转矩系数；d_F为阀杆直径（mm）；F₀为全关时阀座的压紧力（N）；J为推力系数；D_MN1为双座阀的上阀座内径（mm）；M为螺阀的不平衡力矩（N·mm）；μ为阀板轴与轴承的摩擦因数；D_MN2为双座阀的下阀座内径（mm）；M′为蝶阀的输出力矩（N·mm）；DN为蝶阀公称尺寸；p₁为控制阀进口压力（MPa）；p′₁为三通（合流）上阀座进口压力（MPa）；F_P为不平衡力（N）；p₂为控制阀出口压力（MPa）；p₂′为三通（分流）上阀座出口压力（MPa）。

如图8-6a所示的单座阀，若p₂=0，则它的允

许压差计算公式推导如下：

由式（8-43）知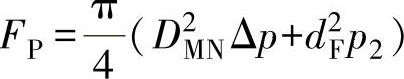

由于p₂=0，于是Δp=p₁，则按式（8-45）得

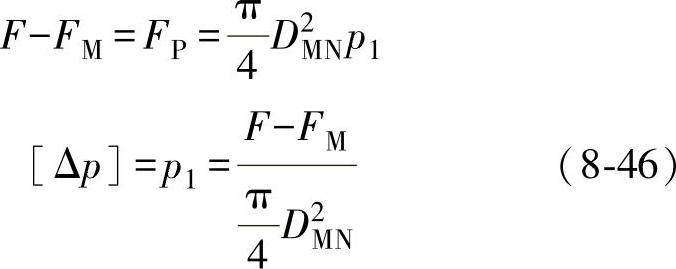
当执行机构和调节阀的大小选定后，就可以求出执行机构输出力F和阀座密封力F_M，再代入式（8-46），便能计算出调节阀两端的允许压差[Δp]。反过来，如果知道[Δp]，就可计算出执行机构的输出力。

各种调节阀的允许压差计算公式见表8-23。

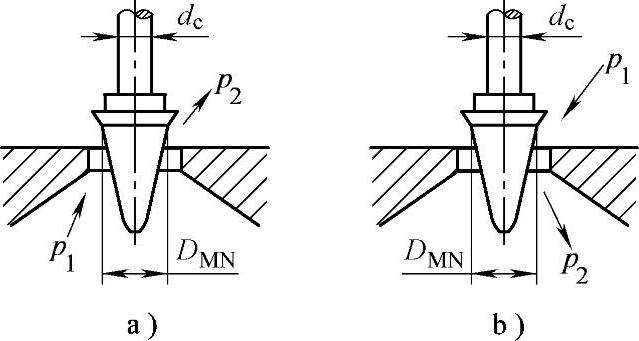
图8-6 单座阀阀芯