气液两相流对调节阀的影响分析

ISA标准中，没有介绍流过调节阀为两相混合物时的计算公式。目前的计算公式基于如下考虑：当两相混合物流过调节阀时，只对气相部分考虑膨胀系数Y，而对液相部分不进行修正。这就是说，当一个气-液混合物通过调节阀时，液体密度不变，而气体密度发生变化。

比较式（7-2）与式（7-31），可得

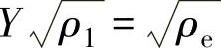
此处ρ_e是在相同条件下，以同样流量通过调节阀的不可压缩介质的有效密度。于是有，ρ_e=Y²ρ₁，此处Y²可看作是可压缩介质的密度修正系数。

将以上考虑应用于亚临界流动情况。此时如以v_g1/Y²作为有效比体积（v_g1是在调节阀入口处的气体比体积），则不可压缩介质流动公式也可应用于气体。“均相混合物”的有效比体积将以w_gv_g1/Y²+w₁v₁表示，此处w_g和w₁是气体与液体组分的质量分数，v₁是液体比体积。

关于通过调节阀的两相混合物的流动方面，做过水和空气的混合物试验。试验结果表明，在大的压力损失下，上述设想由于在喉管处发生的物理现象，而不再有足够的精确性。假如在阀芯系统区内，介质的压力损失降低到低于汽化压力，则一部分液体将发生汽化。在此情况下，按上述假定计算出的流量，将大于实际流量。

如果气体代表连续相，则在X=F_kX_T时，将出现紊流。如果液体是连续相，则当X大于由式F²_L（1-F_Fp_v/p₁）得出的计算值时，将出现节流。

【例7-10】 已知下列数据：介质是水和空气的混合物，空气流量q_m=210kg/h，水流量q_m1=9080kg/h，p₁=0.68MPa，Δp_r=0.25MPa，T₁=25℃，D_c=80mm。试选择所需要的调节阀。

解 “均相混合物”的有效比体积计算如下：

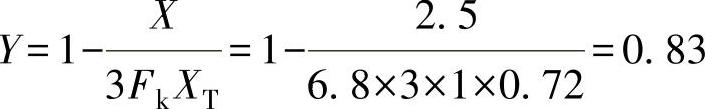
试选单座调节阀，X_T=0.72（表7-4）。

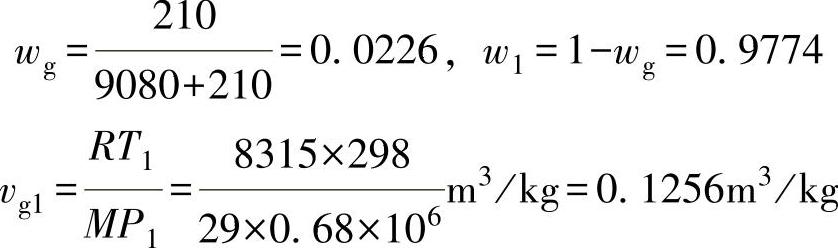
v_e=w_gv_g1/Y²+w₁v₁=（0.0226×0.1256/0.83²+0.9774×0.001）m³/kg

=0.0051m³/kg=5.1L/kg(www.xing528.com)

由式（7-2）推得

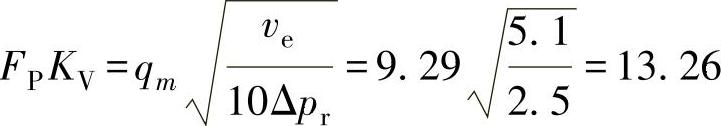
采用K_Vs为20、DN40、D_s=32mm、X_T=0.72的单座调节阀，并验算F_P。

∑ζ_i=ζ₁+ζ₂=1.5（1-（D_r/D_c）2）2=1.5×（1-（40/80）2）2=0.8437

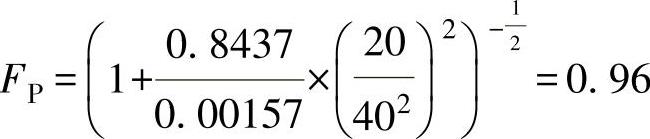
由此可求出所需K_V值为

K_V=K_Vs/F_P=13.26/0.96=13.81

可见采用的调节阀是合适的。

液体和蒸汽混合物的情况，要比气-液混合物的问题复杂得多。问题在于蒸汽与液体之间有质量的传输和能量的交换。从调节阀进口到喉管之间，流动过程是近于等熵的。对于调节阀总体来说，也是等熵的，这是蒸汽-液体混合物流动的重要特点。例如，直到喉管处液体趋向于汽化或凝结，而在压力恢复区总是在汽化。

按照和气-液混合物流动相似推理，可以认为节流受不同因素控制，它取决于由液体还是由蒸汽形成连续相。

当蒸汽在混合物中的质量分数低于3%时，问题更为复杂。例如，对于p=0.68MPa的水和蒸汽的混合物，当x=0.1（蒸汽）和x=0.02时，造成混合物比体积的变化约70%。反之，对于p=0.68MPa的水-蒸汽混合物系统，当x=0.98与x=0.99时，造成的混合物比体积的变化仅为1%。这个例子说明，调节阀入口处蒸汽-液体混合物中，蒸汽含量的准确性对选调节阀的影响。这使得在低蒸汽含量时的问题尖锐化。

由于上述原因，对于气-液混合物，尤其在蒸汽含量低的情况下，建议避免采用调节阀。如无法回避时，对于蒸汽含量高的混合物，建议采用式（7-31）计算。此时以式v_e=w_gv_g1/Y²+w₁v₁计算有效比体积。对于低蒸汽含量的情况，则建议以调节阀入口混合物比体积作为有效比体积，以式（7-16）计算。这时要考虑到，可能会有较大的误差。