可压缩介质调节阀的计算方法优化指南

如前所述，可压缩介质通过调节阀时，可能达到临界速度。对于调节阀结构和调节阀的安装方式，从截面积的变化来说，是沿着流向成收敛-扩散型[拉瓦尔（Laval）喷管]的。已经证明，在收敛-扩散型喷嘴（图7-12b）中，可以达到声速或超声速；而在等截面喷嘴（图7-12a）中，不可能出现超声速。

在喷嘴的临界速度截面上，也就是在速度等于当时温度。压力下介质声速的截面上，应满足式（7-30）：

式中，p_er为达到临界速度v_er时截面上的压力；κ为等熵指数，不同介质的κ值见表7-3。

表7-3中列出了不同介质的临界压力比值p_er/p₁和κ值。

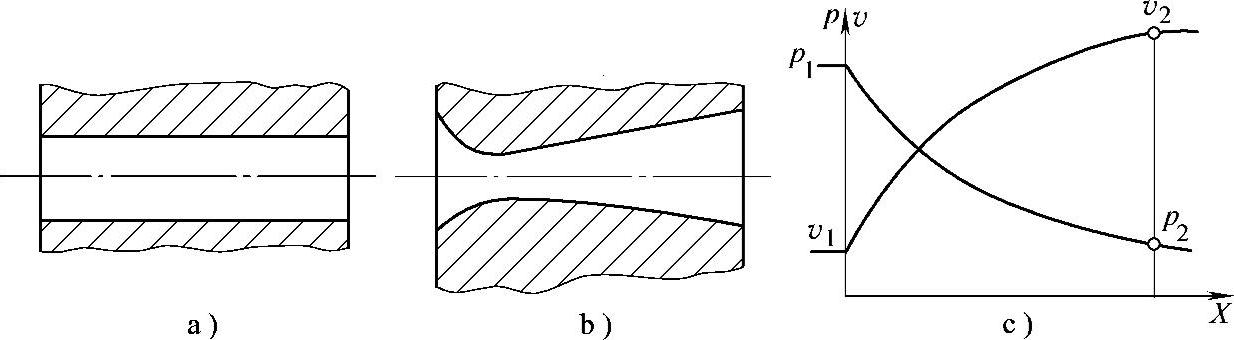
图7-12 可压缩介质流经喷嘴时压力和速度的变化

a）等截面喷嘴 b）拉瓦尔喷嘴 c）压力和速度的变化

当在标准调节阀的喉管处达到声速时，在调节阀的圆柱部分，压力与速度不变，如图7-13所示。但在扩散段，犹如拉瓦尔喷嘴，介质受到很大的加速度而达到超声速。因为在阀后管道中压力为p₂，并处于正常流速（30～50m/s），因而在来自扩散段的超声速射流与管内介质之间，产生强烈的冲撞。此后，超声速度成管内正常流速。这一冲撞引起强烈的噪声，它成为调节阀在临界工作区的特征。

表7-3 不同介质的临界压力比p_er/pt

对于角式调节阀，情况更为恶化。它的阀座与连接法兰之间形成扩散段。这一扩散段和阀后大小头加在一起，形成一个比较标准调节阀更长的扩散段。因此在临界流动区内，达到比标准调节阀更高的超声速，从而引起更强烈的撞击（图7-14c）。

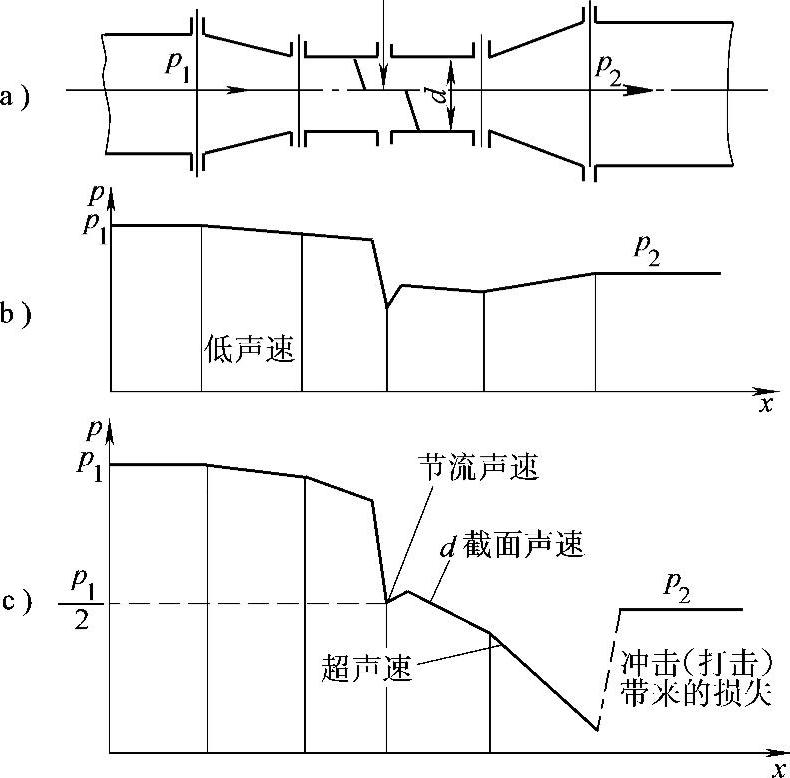
图7-13 标准调节阀的压力变化

a）调节阀示意图 b）亚临界流的压力变化 c）超临界流的压力变化

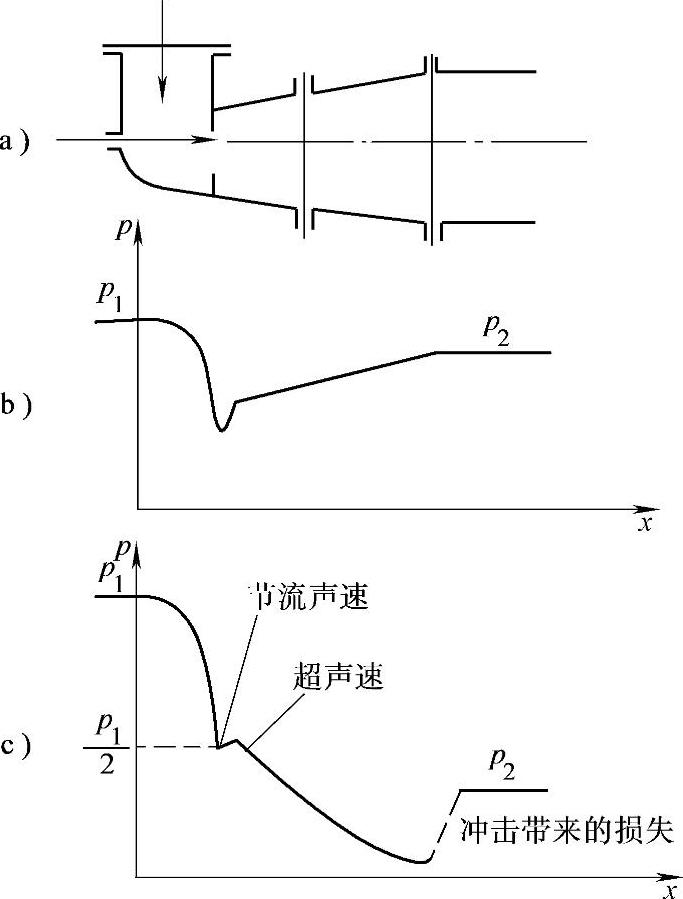
图7-14 角式调节阀中压力的变化

a）调节阀示意图 b）亚临界流压力变化 c）超临界流压力变化

由此可见，阀后大小头在亚临界情况下，是作为一个动能变为压力能的正常能量变换器（图7-13b及图7-14b），而在临界流区，起相反作用。

下面将介绍用于气体及蒸汽的ISA计算公式。通过调节阀的气体或蒸汽的流量可用下列公式计算：

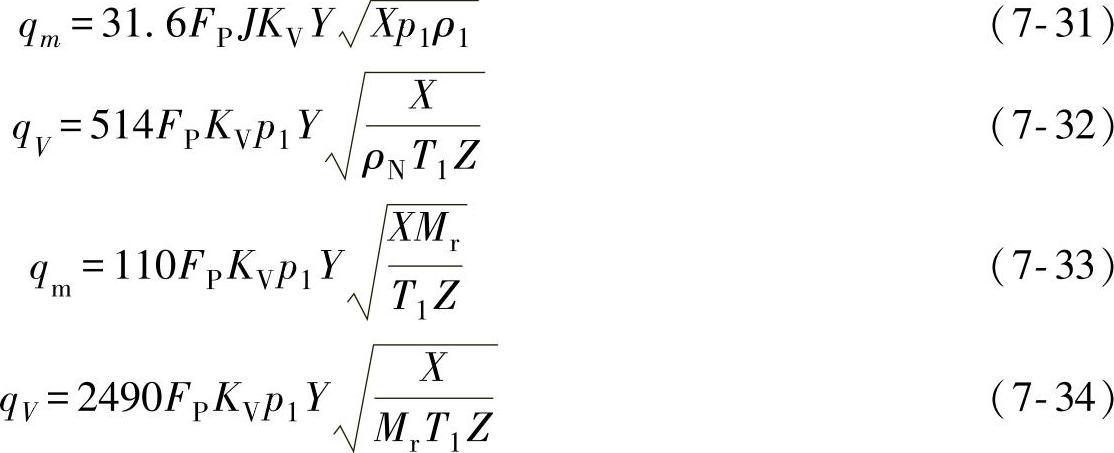
式中，X为相对压力损失，X=Δp_r/p₁，p₁是绝对压力；ρ₁为调节阀前气体密度（kg/m³）；ρN为在标准状态下，气体对空气的相对密度；Z为压缩系数（对理想气体Z=1）；T₁为调节阀前气体温度（K）；M_r为相对分子质量；Y为膨胀系数。

膨胀系数的定义是指在相同雷诺数下，可压缩性介质的流量系数与不可压缩介质的流量系数之比。它可由式（7-35）计算：

式中，X_T为Y取小限值0.667时的X值；F_κ为等熵指数κ和1.4之比。

F_κ=（c_p/c_V）/1.4=κ/1.4 （7-36）

由此可见，式（7-31）～式（7-34）都含有Y。它的推导是基于流过喷嘴的流动现象。通过Y的计算，可以求得式（7-31）至式（7-34）各式的值。

1.膨胀系数

膨胀系数Y是考虑从调节阀进口到喉管处，可压缩介质密度变化的影响而引入的喉管压力损失，随面积收缩而变化，因此也称为“收缩系数”。

收缩系数的值一般小于1.0而大于0.667，它在理论上受以下因素影响：

1）调节阀喉管处面积和进口面积之比。

2）调节阀通道形状。

3）Δp_r/p₁值。

4）雷诺数Re。

5）c_p/c_V值。

前3个因素的影响以X_T表示，它通过试验或由F_L决定。进行试验的结果表明Y和X之间的关系是线性关系，可用式（7-35）表示。

在实际情况下，对于可压缩性介质，雷诺数超出Y的影响范围。

等熵指数κ=c_p/c_V，影响直线Y=f（X）的斜率。这个影响以系数F_κ表示，对空气，F_κ=1。工业上常用的各种气体的κ值见表7-3。

2.相对压力损失系数(www.xing528.com)

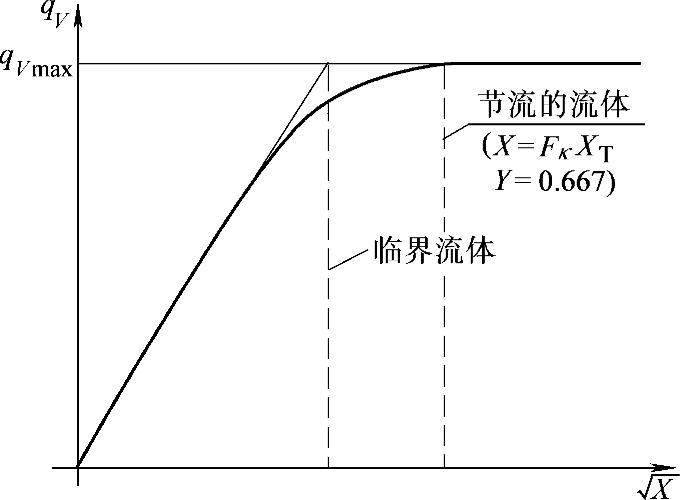
图7-15 q_V=f（X）的函数关系

若调节阀前压力p₁为一定，而调节阀后压力逐渐降低，则流量开始逐渐增大到某一限度（图7-15）。当p₂继续降低时，流量不再增加，当X=F_κX_T时，就达到极限，此时Y=0.667。对于空气（ρ_N=1），在无大小头情况下（F_P=1），式（7-32）变为

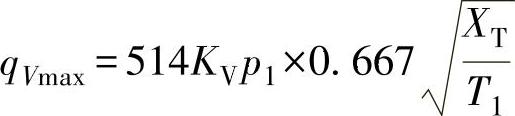
即

式（7-37）可用以确定X_T，表7-4列出了X_T的代表值。

表7-4 在H₁₀₀及D_s=D_r情况下，系数X_T的代表值

如果调节阀采用大小头，X_T值有所不同。此时可利用式（7-38）计算：

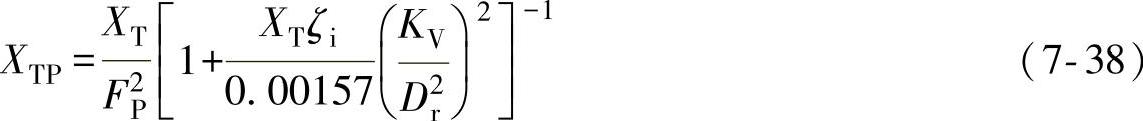
系数X_T与取决于液体流动的系数F_L之间的关系式为

X_T≈0.84F²_L （7-39）

【例7-7】 已知数据如下：q_m=9000kg/h，ρ₁=43.5kg/m³（氟利昂），κ=1.14，p₁=0.8MPa，p₂=0.38MPa，管子直径D_c=50mm。试选择所需要的调节阀。

解 设选用具有周边仿形阀芯的单座调节阀，

X_T≈0.72（查表7-4），计算如下：

X=Δp_r/p₁=0.42/0.8=0.525

F_κ=κ/1.4=1.14/1.4=0.814

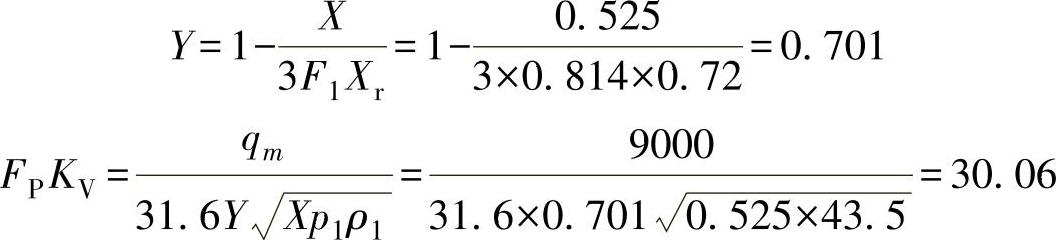
由此可见，应选用周边仿形阀芯的单座调节阀，DN50，K_Vs为40，无大小头（F_P=1）。

【例7-8】 已知数据：介质为水蒸气，p₁=8.0MPa，p₂=1.5MPa，T₁=300℃，T₂=225℃，q_m=25000kg/h，p_c=22.1MPa，T_c=374℃，阀前管径100mm，阀后管径150mm。试决定所需调节阀的尺寸。

解 试选用具有周边仿形阀芯的角阀，X_T=0.72，计算如下：

X=Δp_r/p₁=6.5/8.0=0.8125

F_κ=κ/1.4=1.32/1.4=0.943

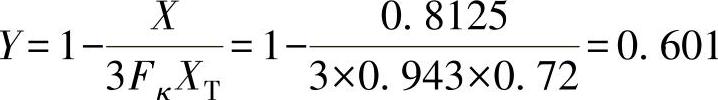
这个值不能满足要求，因为前面已指出，Y的最小值是0.667（X=F_κX_T=0.943×0.72=0.679）。

p_r=p₁/p_c=8.0/22.1=0.362

T_r=T₁T_c=（300+273）/（374+273）=0.885

当p_r=0.362、T_r=0.885时，Z=0.77。

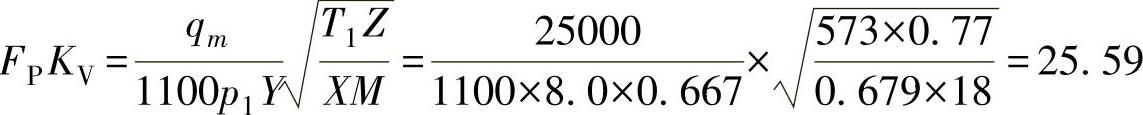
故选用一个DN50的调节阀，K_Vs为36，D_s′=40mm。

下面继续计算：

∑ζ₁=0.5[1-（D_r/D_c）²]²+[1-（D_r/D_c）²]²+1-（D_r/D_c）⁴-[1-（D_r/D_c）⁴]

=0.5[1-（50/100）²]²+[1-（50/150）²]²+1-（50/100）⁴-[1-（50/150）⁴]

=1.02

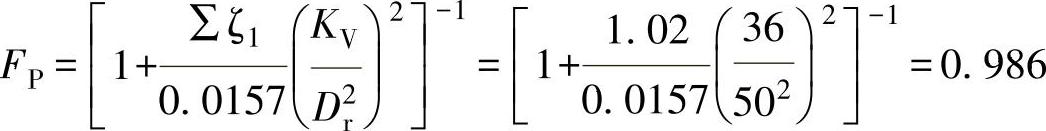
F_PK_Vs=0.986×36=35.496>25.59

显然，从流通能力来说，所选调节阀是能满足要求的。