电动执行机构力的计算方法及应用

在电动执行机构中，阀门的开启和关闭速度、传动轴的转动力矩，决定于电动机的转速、功率和传动机构的传动比。当载荷恒定时，由于闭路阀突然停止转动，电动机传动轴的转动力矩会因为电动机转子的动能作用而急剧增加。为了限制力矩，采用离合器或过电流保护继电器。

在进行离合器的受力计算时，最重要的是凸轮机构的计算。图6-19所示为作用在凸轮机构上的力。这是凸轮机构的凸轮顶住离合器上的圆盘工作时情况。当转动力矩达到一定数值时，圆盘转动压缩弹簧，而心轴（滚子）被压退，并沿着构成平面之圆盘的边缘滑动。

为了具有必需的力矩，并尽可能使其数值保持恒定，因而问题在于确定必需的弹簧作用力、盘件的半径和凸轮的外形。

沿着垂直的轴心线方向的弹簧作用力F_n，由切线为A—A的倾斜面所承受。切线A—A与弹簧作用力和心轴的引导方向成90°+α角。弹簧的作用力F_n可以分解为作用于轴线上的力F_r和F_N，并且F_N与心轴引导方向的反作用力和盘件上的反作用力F_R相抵消。

圆盘上的作用力F_N，可以分解为F_n和F，其中F=F_ntanα。

图6-19 作用在凸轮机构上的力

由于力F_n而作用于圆盘上的力矩为

M=F_nrtanα

可以利用圆盘和心轴（滚子）的功率恒等式求出力矩M：

Mω=F_nv

故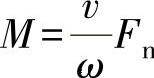

式中，v为垂直心轴（滚子）的移动速度；ω

为圆盘的旋转角速度。

但 v=v_r+tanφ

式中，v_r为圆盘上M点的圆周速度。

因为 v_r=rω

故有 v=rωtanφ

由此可得

假如r和φ为已知，则利用此式很方便。

由于 和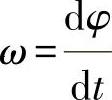

故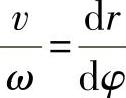

所以

由此得出

r_M含义如图6-19所示。

由此可见，若需M和F_n为恒定值，凸轮工作外形应做成阿基米德螺旋线。

在实际条件下，弹簧作用力F_n随着弹簧的刚度和挠度而改变。

假定弹簧作用力为F_M时，心轴（滚子）相应位于半径r_M处，而r_δ处的作用力相当于F_δ，则弹簧的刚度为

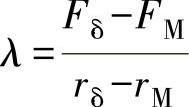
由此得 F_n=F_M+λ（r_δ-r_M）

则

或 Mdφ=[F_M+λ（r_δ-r_M）]dr_δ

微分后得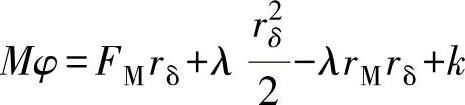

由r_δ=r_M的条件，在φ=0时确定常数k，得

故

凸轮外形方程式可写成如下形式：

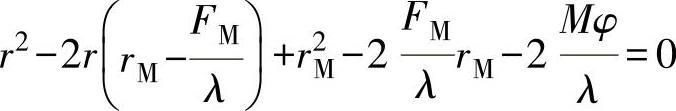
由此得

利用式（6-13）可绘制出凸轮外形。弹簧的刚度和挠度基本上可由以下公式确定：

弹簧刚度

在作用力由F_M到F_δ范围内的弹簧挠度为：

其中 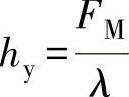(www.xing528.com)

压力角α的计算式为

通常凸轮机构有心轴（滚子），因此所作出的曲线可以看作是心轴（滚子）中心的运动轨迹，而凸轮的外形做成其距离等于心轴（滚子）半径的等距曲线。

可以用通过三点的近似圆弧来代替准确的曲线。绘制用来代替准确曲线的半径为

R²=ρ²+r²_c-2ρr_ccosφ_c

其中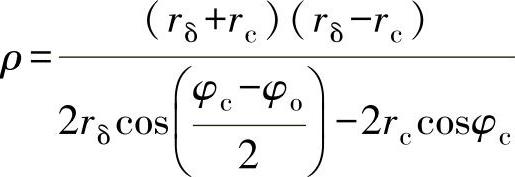

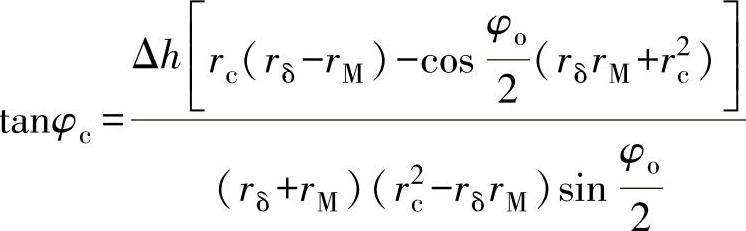
r_c的数值可以用r和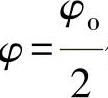代入公式确定。

设计控制转矩离合器时，最好使用阀门开启时所限用的力矩，比关闭时大20%～25%。这样可以考虑到静摩擦因数的作用，保证阀门可靠开启。

端部凸轮的外形应设计成螺旋线形，其剖面形状与在其上滚动的滚子相适应。

不考虑过载和电动机转子起动能作用的静力计算时，电力执行机构的受力计算可以归结如下：

1）确定必需的传动减速装置的总传动比i：

式中，n为电动机转速（r/min）（在正常载荷情况下）；n_B为控制阀门传动轴转速（r/min）。

根据传动齿轮的对数与结构，总传动比可以分解为符合下述条件的传动比：

i=i₁i₂i₃…i_n

式中，i₁、i₂、i₃、…、in为单级传动比。

2）根据减速器类型、传动比，以及工作性质（是否有油槽、非封闭传动等），确定其传动效率：

η=η₁η₂η₃…η_n

式中，η₁、η₂、η₃、…、η_n为单级传动效率。行星机构传动的效率，不等于任意单个传动效率的组合。

阀门传动机构计算中，采用一对齿轮时的效率值见表6-13。

表6-13 阀门计算中采用一对齿轮时的效率值

3）确定电动机所必需的功率。对于阀门的传动，最常采用高转差率AOC型封闭环吹式三相异步电动机。这种电动机最适宜于带冲击载荷的周期性工作。

图6-21所示为三相异步电动机的机械特性曲线。从图中可以看出，转速n取决于旋转力矩M，而旋转力矩取决于转差率S。

转差率S的计算式为

式中，n_C为取决于电流频率（每秒钟周数）和电动机磁极圈数的同步转速；n为实际转速。

当同步转速n_C=1500r/min时，随着电动机功率的不同，AOC型电动机在公称功率时，n_N=1300～1395r/min。

图6-20a的图线n=f（M）示出，异步电动机容许有比公称转矩M_N较大的超载力矩。对于所述及的电动机，其起动力矩可超为公称力矩2.2～2.3倍，即

M_Q=（2.2～2.3）M_N

最大转矩M_max大于公称力矩2.3～2.6倍以上。因为在闭路阀内，最大载荷产生于阀门关闭的末期，或开启的初期，而且这个时间通常甚短。电动机的选择最好考虑到过载系数K_n，其值见表6-14。

图6-20 三相异步电动机的特性曲线

a）n=f（M） b）M=φ（S）

表6-14 过载系数Kn

电动机的功率P（kW）可按式（6-14）计算：

式中，M_B为传动轴的输出力矩（N·m）；n_B为传动轴的转速（r/min）；η为传动装置的总效率。

为了经济起见，电动机的功率可按式（6-15）计算：

式中，P_P为电动机的计算功率（kW）。

根据所得出的功率P_B，按产品目录选用具有与计算功率相近的电动机。但所选用的电动机的功率不得小于P_P的20%，在有的情况下，应该选用功率比P_B大的电动机。