气动薄膜执行机构的应用和优势

气动薄膜执行机构是最常用的机构，传统结构如图3-54所示。它的结构简单，动作可靠，维修方便，价格低廉。

气动薄膜机构分正作用式（图3-54a）和反作用式（图3-54b）两种。国产型号为ZMA型（正作用）和ZMB型（反作用），信号压力一般为20～100kPa，气源压力为0.5～0.7MPa，信号压力增加时，推杆向下动作的叫正作用执行机构；信号压力增加时，推杆向上动作的叫反作用执行机构。正、反作用执行机构基本相同，均由上下膜盖、波纹薄膜、推杆、支架、压缩弹簧、弹簧座、调节件、标尺等组成。在正作用执行机构上，有一个装O形密封圈的填块。只要更换个别零件，即可变为反作用执行机构。

这种执行机构的输出特性是比例式的，即输出位移与输入的气压信号成比例关系。当信号压力通入薄膜气室时，在薄膜2上产生一个推力，使推杆5移动并压缩弹簧6。当弹簧6的反作用力与信号压力在薄膜2上产生的推力相平衡时，推杆5稳定在一个新的位置。信号压力越大；在薄膜上产生的推力就越大，则与它平衡的弹簧反力也越大，即推杆的位移量越大。推杆的位移就是执行机构的直线输出位移，也称为行程。

图6-1 阀门定位器和执行机构的方块图

国产气动薄膜弹簧执行机构的行程规格有10mm、16mm、25mm、40mm、60mm和100mm等。薄膜的有效面积有20000mm²、28000mm²、40000mm²、63000mm²、100000mm²和160000mm²六种规格。有效面积越大，执行机构的位移和推力也越大，可根据实际需要进行选择。

1.橡胶薄膜执行机构力的计算

橡胶薄膜执行机构力的计算，应先根据已知行程确定薄膜的直径。设计时，建议采用尺寸最小的薄膜。这样就可以使用作用力最小的弹簧，但这种条件并不能经常得到保证。

在进行计算时，最重要的是确定取决于薄膜挠度的膜片拉力，或调位时的作用力。

由薄膜传给阀杆的作用力F_g，应小于压力p作用于直径为D的圆面积上所引起的力。作用力F_g的大小，取决于尺寸D及d、橡胶性质和薄膜的类型。可用式（6-1）确定：

F_g=pA_g （6-1）

式中，p为介质压力（MPa）；A_g为薄膜的有效面积（mm²）。

由此确定有效面积A时，应考虑到上述各种因素的影响。

由几何形状的关系，可以得出下面关系式

式中，D为封闭处圆周的直径（mm）；d为薄膜圆顶的直径（mm）。

若薄膜行程不大于±5%D，在进行闭路阀传动装置的受力计算时，可以采用上式近似地定出A_g。在进行调节阀计算时，要求更精确地确定A_g值。

上述关系可以用试验研究的方法加以证实。因此，建议采用下列试验公式：

F_g=φCpA （6-2）

式中，A为从封闭处直径开始计算的薄膜面积（mm²），A=0.785D²；C为不均匀性系数；C为考虑到A_g的变化不均匀性系数，取决于薄膜刚度的影响；φ为薄膜挠度为零时（薄膜处于中间状态时）的有效系数。φ为杆部有效作用力与由介质压力作用于薄膜的总作用力之比，当C=1时，，而F=pA。

对于厚度由3～5mm，直径D=100～300mm的带布垫和不带布垫的平面薄膜，其有效系数φ的关系式如下（图6-2）：

φ≈0.14+0.8k

其中 k=d/D

上述关系式在压力0.1～0.8MPa的范围内是实用的。

对D≤160mm和D>160mm的薄膜，不均匀性系数C的数值是不同的：

1）对于D≤160mm带布垫的薄膜，可以取（精度可达±10%）

当k=0.8时，；

当k=0.7时，；

当k=0.6时，。

式中，h为薄膜相对于中间距离的移动。

图6-2 平面橡胶薄膜的有效系数φ

1—用公式求得的面积曲线

2—用公式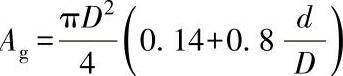求得的面积曲线

2）对于不带布垫的D≤160mm的薄膜，所有k值都取C=1。

3）对于带布垫和不带布垫的D>160mm的薄膜，经常采用k=0.6～0.8时，其不均匀性系数为

用“+”号时应当注意，当薄膜相对于其中间位置移动时，若其移动方向使作用于薄膜上的介质容积减少（图6-3位置Ⅰ），取“+”号；若薄膜移动方向使介质的容积增加（图6-3位置Ⅱ），则取“-”号。

图6-3 用于橡胶组合式薄膜的不均匀性系数C

平面组合式薄膜由下述方法得出：

将薄膜固定在零件上，使其不呈平滑表面而有袋状松弛处。为此目的，应将菌状顶片顶紧或放松，然后再将薄膜固定在法兰盘之间，或者用螺栓穿过分布于薄膜大圆周上的孔，固定在阀体和阀盖之间。

试验结果确定，当的值由0.8到-0.8时，压力小于1.2MPa，薄膜厚度在5～7mm之间。D=90～130mm的单层橡胶制成的、带单层布垫的薄膜，其不均匀性系数可以近似取为

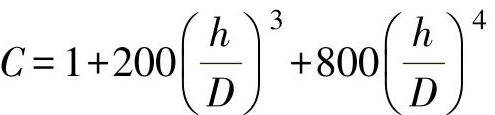
图6-3薄膜处于位置Ⅱ时，h为负值；薄膜处于位置Ⅰ时，h为正值。

膜压式薄膜的某些试验结果列于图6-4。

利用式（6-3）进行橡胶薄膜的强度计算

0.7pAk=πDδ[σ_τ] （6-3）

式中，p为作用于薄膜上的介质压力（MPa）；A_k为环形的面积（mm²），A_k=0.785（D²-d²）；δ为薄膜的总厚度（mm）；[στ]为橡胶许用切应力（MPa）。

根据断裂强度σ=5.0MPa的橡胶试验结果确定。若利用此种橡胶做成带单层布垫的薄膜，其许用切应力见表6-1。

表6-1 带单层布垫的橡胶薄膜的许用应力

薄膜行程选择时，对于平面式薄膜，建议厚度不大于0.15D；对于膜压式薄膜，建议厚度不大于0.20D。

菌状顶片的直径d，根据杆上必须的作用力及此力变化范围的大小而定。薄膜的有效面积随比值的增加而增加，但在给定作用力变化范围内，其允许行程会减小，或者在给定的行程内，其作用力的变化增大。通常用得最多的是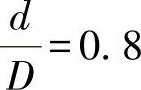。有时为了能得到比较均匀的作用力，可采用。

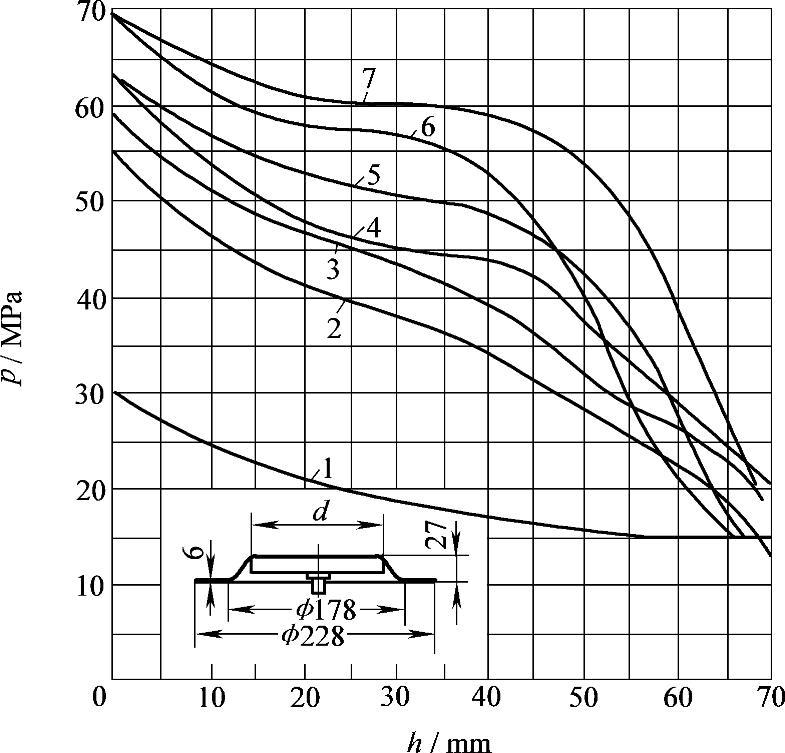
图6-4 杆上压力p的变化与薄膜行程的关系（用于模压式薄膜）

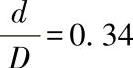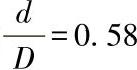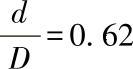注：1曲线的；2曲线的；3曲线的；4曲线的；5曲线的；6曲线的；7曲线的。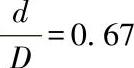

调节阀的薄膜执行机构，通常在很多情况下是按图6-5工作的，即有一种由于膜片回弹所形成的必然的关系

h=f（p）式中，h为阀瓣移动距离（mm）；p为工作介质压力（MPa）。图6-5所示的调节阀传动装置中，需要尽量准确保证的条件是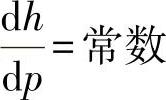。即h=Cp，从而可以使用有效面积尽可能不变的薄膜和特性曲线很接近于直线的弹簧。为此目的，可以采用行程比较小的薄膜，而弹簧则靠于推力轴承上，以免由于摩擦力而引起弹簧的附加扭转。

在图6-5b中，由于空气的压力作用于薄膜上，根据薄膜的行程，坐标的起端和末端的作用力相应为

F₁=p₁A_0gF_n=p_nA_0g

式中，p₁、p_n为行程起端和末端时作用于薄膜上的压力（MPa）；A_0g为挠度为零时，薄膜的有效面积。

在图6-5b中，带倾斜角α的直线Ⅰ—Ⅰ的斜率为

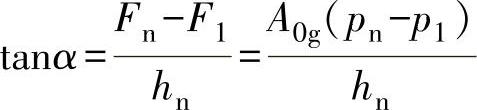
图6-5 气动薄膜执行机构的结构图和计算图

a）结构图 b）计算图

作用在图6-5b上的恒定作用力如下：

1）F_p+F_mn为由调节阀内压力损失、作用于阀座上部和底部面积差上的力和推动阀杆的力所组成。此力作用于弹簧活动的方向，因而标在图中零线的上方，并得出横线Ⅱ—Ⅱ。

2）F_G为装在阀杆上的零件重力。此力的作用方向与弹簧活动方向相反（将调节阀处于垂直位置时常有的情况），因而将其标在横线Ⅱ—Ⅱ的下方，并得出横线Ⅲ—Ⅲ。

3）坐标段Ⅰ—Ⅲ给出弹簧作用力的必需值，其中，F_ycm为作用于行程起端的力；F_paδ为作用于行程末端的力。

在装有气动执行机构的调节阀中，最常采用的是p₁=0.02MPa，p_n=0.1MPa。

填料和阀瓣导向部分及阀杆和执行机构的摩擦力F_f形成一定的阀门不敏感区，在不敏感区内，当阀杆上的作用力在小于2F_f的范围内变动时，阀杆的运动方向不变。沿线Ⅰ—Ⅰ加上2F_f值而得出处于线Ⅳ—Ⅳ和Ⅴ—Ⅴ区内的阀门不敏感区。由此，在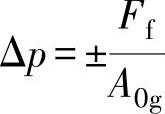范围内，压力的变化不会导致阀杆运动方向的改变。为了使阀杆反向运动，压力的变化常达2Δp。因此，阀瓣位置的极限偏差。在压力为p的情况下改变阀杆的运动方向时，阀杆的位置差别将为2Δh。

进行进一步核算时，应考虑到弹簧的非线性极限偏差和行程变化的薄膜的有效面积的改变。

弹簧挠度增加时，其受压刚性有些降低，因此整个弹簧的刚度应降低。这对长的弹簧是正确的。对于较大刚性的短弹簧，阀门传动采用这种弹簧，随着载荷的增加，弹簧圈的刚性降低，而弹簧的刚度不降低；反之，由于在工作时圈数的减少，因为螺旋最初在全部长度上和螺旋的支持点接触，故弹簧的刚度随挠度的增加而增加。因此，校正后的弹簧特性将是一条曲线，如图6-6a中虚线所示。假如用直线3代替计算所得的特性线1，就将在两直线间产生α₁角，则在行程中途的工作误差有少许增加，而其最终作用力将与计算所得的特性线重合。

平面式和膜压式橡胶薄膜的有效面积不是恒定值。在行程起始时，其值较大，而在行程末期则具有较小的数值。只有当薄膜挠度近于零时，才能保持A_g的稳定性。如图6-6b所示，用倾斜角为α₂，连接图中A—A两点的直线A—A，来代替图中的水平直线，可以得到较为精确的计算结果。

图6-6 计算薄膜执行机构校正曲线

a）弹簧影响区 b）薄膜的影响 c）薄膜和弹簧的综合影响

1—计算特性曲线 2—校正后的特性曲线 3—近似特性曲线 4—当A_g为常数时作用力F为恒定值 5—当p为常数时薄膜的实际特性线F=f（h） 6—薄膜近似特性线 7—所要求的理论图线 8—弹簧作用力的变化，F=f（h） 9—薄膜上作用力的变化

为了进行更精确的计算，最好按图6-6b中A—A的有效面积来绘制Ⅰ—Ⅰ线（图6-5），而弹簧的特性线则按图6-6a中的直线3绘制，由此可得出图6-6b。其中直线1为F=ch的理论直线性图形，直线2表示出行程为h时弹簧作用力的变化，曲线3示出当压力按直线1变化时薄膜上作用力的变化。

由图6-6c看出，在所讨论的条件下，可以保持A点和B点具有所要求的压力，但不能保持AB之间过渡点上图形的直线性。

考察一下挠度为h_T时的任意点M。在M点，将出现作用力F_φ来代替弹簧的理论作用力F_T。在某一给定h值时，薄膜的有效面积比所必需的要大，因此需要在压力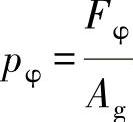时才能保持平衡。其中，A_g是行程为h时的有效面积。p_φ值在纵坐标上（垂直方向）形成不均匀间距，利用弹簧作用力的变化和取决于行程的薄膜有效面积可以做出校正图，h=f（p）或者p=φ（h）。

薄膜行程与作用力在比例关系上的极限偏差，可由下法确定：当压力为p_T时，在M点上，实际的薄膜行程（传动行程），不等于理论行程h_T，而要小Δh。其近似值为

此时，薄膜上的实际压力为

在调节阀内，除了所论及的作用力外，还产生液流作用于阀瓣上的水力，以及阀瓣折损时的力矩。前者形成阀瓣柱塞的轴向力，试图关闭阀门。上述的作用力可达很大数值，对阀门工作的影响严重。这些作用力不能用理论计算，必须由试验确定。

2.调节阀压缩弹簧的计算

在调节阀上，通常都选用圆柱形螺旋压缩弹簧作为调节元件。按弹簧的使用要求，调节阀使用弹簧采用一级精度，其变形的极限偏差应小于标定牌号的±10%。计算时，应首先确定弹簧的最大工作负荷，据此再确定弹簧钢丝的直径。亦可以根据结构情况，先选定标准弹簧，然后再进行核算。

（1）调节弹簧的载荷 从力的平衡关系，可以得出调节弹簧的载荷为

式中，F_t为调节弹簧的载荷（N）；p_c为调节阀的出口压力（MPa）；d_f为副阀座内径（mm）；p_J为调节阀的进口压力（MPa）；F_fa为副阀瓣弹簧的安装载荷（N），其值取副阀瓣重力的1.2倍；λ_f为副阀弹簧的刚度（N/mm）；H_f为副阀瓣开启高度（mm）；A_m为受压薄膜的有效面积（mm²）。

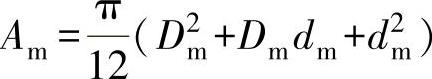
式中，D_m为薄膜的有效直径（mm）；d_m为调节弹簧垫块直径（mm）。

（2）螺旋压缩弹簧应力的计算 作用在弹簧上的静作用力F_t，所产生弹簧金属丝横断面上的剪切和扭转总应力的计算式为

括号中的“1”可忽略不计，因为和第二部分比较很小，故得到近似公式为

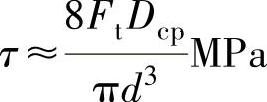
式中，τ为弹簧的切应力（MPa）；F_t为调节弹簧的载荷（N）；D_cp为弹簧的平均直径（mm）；d为弹簧钢丝直径（mm）。

弹簧的变形量为

式中，F_t为调节弹簧的载荷（N）；D_cp为弹簧的平均直径（mm）；n为弹簧的圈数；d为弹簧钢丝直径（mm）；G为切变模量（MPa）。

为考虑到附加因素的影响，采用修正系数，得到的应力公式为

系数K₁为

其中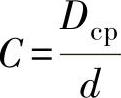

取决于C的K₁值见表6-2。

弹簧的变形量还可以用式（6-4）计算：

其中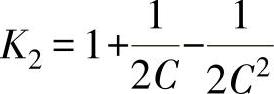

表6-2 不同C值时的K₁和K₂值

取决于C的K₂值见表6-1。

弹簧在正常工作时的C值范围为4≤C≤12，在特殊情况下达到3≤C≤20。

在计算弹簧时，根据载荷F_t产生的变形，可用图6-7清楚地表示，并利用图表可以求出弹簧的参数。

实际的曲线和理论曲线有些不同，如图6-8所示。

对于长的弹簧，当增加载荷时，由于螺旋倾角减小，弹簧的刚性有些降低；对短的弹簧则相反，当载荷增加时（弹簧受压），由于工作圈数减少，弹簧刚度增加。

图6-7 弹簧压缩时力的变化

F₁—弹簧的预压缩力（F₁相应于在机构中工作时的最小力） F₂—弹簧在工作过程中的最大力 F₃—弹簧压缩到弹簧末圈接触时的作用力 F_n—试验的载荷 d—弹簧的钢丝直径 D、D₁、D₂—弹簧的内径、中径、外径 H—弹簧的自由长度 t—弹簧圈之间的距离（节距） f₁、f₂、f₃—弹簧受力F₁、F₂、F₃的变形量 δ—弹簧圈之间的间隙

在计算弹簧时，一般采用的许用应力比较大。通常情况下，钢许用应力为4.0～13.5MPa，青铜许用应力为3.0～4.5MPa。

许用应力的大小取决于金属丝材料，同时也随直径而变化。因为小尺寸的金属丝经拉伸可获得较高的力学性能。轧制材料的许用应力不取决于直径。

在计算弹簧时，由不同材料所采用的计用应力值见表6-3、表6-4及表6-5。

（1）冷轧碳素钢制造的弹簧 为了消除内应力，根据金属丝的直径，在240～260℃中保持10～30min，在空气中冷却。

（2）碳钢制造的弹簧 应在油中淬火冷却。加热温度：60Si2钢的为820～840℃；50CrVA钢的为850～860℃，40Cr13的为1000～1100℃。加热时间，根据弹簧金属丝的直径在8～30min的范围内。由碳钢制造的弹簧淬火后，应在盐浴池中加热。加热温度：60Si2钢的为400～425℃（硬度为48～52HRC）；50CrVA的为400～420℃（硬度为46～50HRC）；40Cr13的为480～495℃（硬度为46～50HRC）。

图6-8 压缩弹簧的特性曲线

1—计算的特性曲线 2—短弹簧校正后的理论特性曲线 3—长弹簧校正后的理论特性曲线

表6-3 碳素钢制造的弹簧许用应力

（续）

①为消除应力，必须回火。

②括号中的尺寸不推荐使用。

表6-4 合金钢制造的弹簧的许用应力

①热处理的[τ]=400MPa，冷拉的[τ]=550MPa。

②冷拉金属丝。

表6-5 青铜制弹簧的许用应力

（3）由12Cr18Ni9钢制造的弹簧 为了消除产生的应力，在400～430℃时保持20～30min，并在空气中冷却。

（4）由硅锰青铜Si2.7～3.5、Mn1～1.5金属丝制造的弹簧 为了消除产生的应力，在120～150℃时保持1～2h，随后在空气中冷却。

（5）铍青铜QBe2制造的弹簧 必须在室温下水中淬火。淬火的加热温度为780℃，保持1～2h。淬火后，根据弹簧金属丝的直径，在325℃下，进行保持2～5h的保温。

为使淬火钢制造的弹簧尺寸稳定，应预先检查材料的力学性能和弹簧热处理的结果。淬火后回火，用将弹簧压缩到螺旋圈未接触的方法；间接加载荷时效6h。

（6）由冷轧碳钢制造的弹簧 在缠绕后，不淬火。为了消除冷作硬化后的应力，应进行6h的加载荷时效，代替螺旋圈未接触时3～5倍的弹簧压缩。

弹簧的防腐层及电镀后，为消除氢所进行的加热，可能是产生弹簧脆性的来源。因此，电镀后的这种弹簧，应将弹簧圈压缩到未接触的情况下，进行24h的加载荷时效。

只有在这种情况下，当用弹簧压缩到弹簧未接触情况下的加载荷时效时，因为不允许有过大的应力，而这种应力，当弹簧在阀门中工作所产生的最大变形值时进行加载荷时效时，是可能产生的。(www.xing528.com)

由于压缩弹簧在轴向载荷作用下工作，因此设计时应保证弹簧纵向稳定性比侧向膨胀要好。弹簧的纵向稳定性取决于比值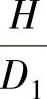，即自由状态时的弹簧长度对弹簧中径的比值。同时，弹簧圈扭转的可能性，决定于末端弹簧圈的固定方法。

应区分两种支撑情况：末端的弹簧圈有相对垂直轴扭转的可能（形式Ⅰ）；末端弹簧圈不可能扭转（形式Ⅱ）。

为使弹簧在不同压缩值下，不丧失稳定性，必须具备下述条件：

按形式Ⅰ固定时

按形式Ⅱ固定时

弹簧的计算一般用一贯近似的方法来解决。为了选用方便，推荐查表6-6，表中F值为当应力τ和每圈的弹簧刚度K₁时，压缩弹簧的载荷。

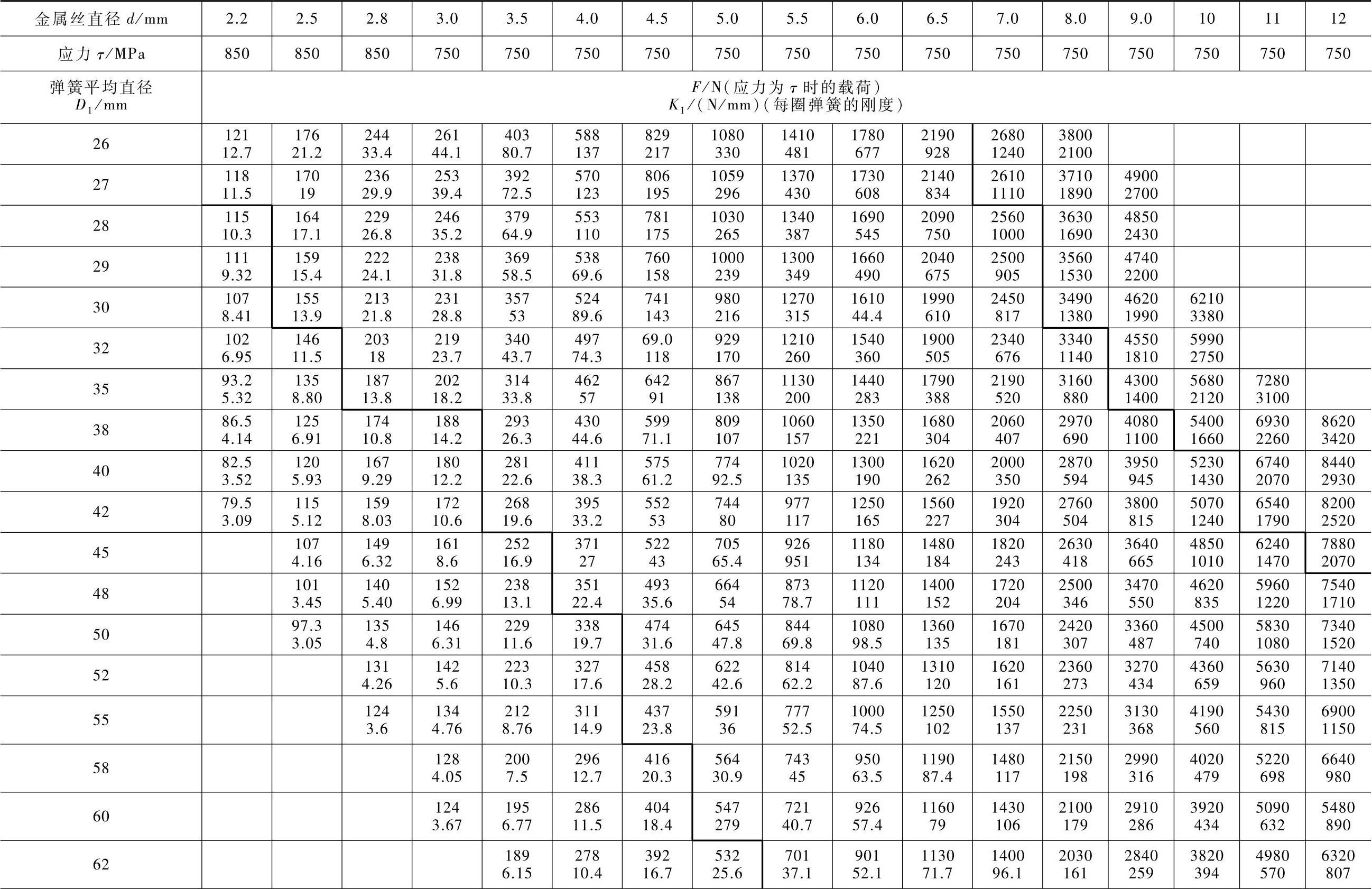
表6-6 压缩弹簧或拉伸弹簧载荷F（上面的数值）和每圈的刚度K₁（下面的数值）（材料为钢，T_N=8OOOOMPa）

（续）

（续）

注：1.对直径1～2.8mm碳钢Ⅱ级金属丝和对直径3mm以上的6OSi2及6OSi2N号钢制的弹簧，T值按许用应力[T]确定。

2.当许用应力[T]=T时，载荷F按弹簧压缩到各圈未接触时的作用力F₃确定。

表6-6中应力值τ，是碳钢Ⅱ级金属丝。当直径为1～2.8mm，和牌号为60Si2及60Si2N钢，直径为3.0mm时的许用应力[τ]相适应的，当许用应力采用别的值时（如其他钢号、青铜和特殊工作条件的弹簧），弹簧压缩到各圈未接触时的作用力F₃按下式确定

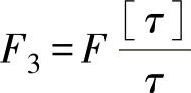
式中，F与τ为表6-6给定值。

同样，表6-6中引用的切应力为τ_N=80000MPa，（在改变系数时）钢制弹簧每圈的刚度数值，在这种情况下，当τ_N为别的值（06Cr19Ni10的τ_N=70000MPa，青铜的τ_N=40000MPa，铍青铜的τ_N=51000MPa）时刚度K₁值按式（6-5）确定：

弹簧节距t通常为

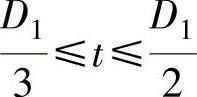
每圈之间的距离δ：d≤5mm时，δ=0.2d；当d>5mm时，δ=0.1d。

螺旋的工作圈数n选用0.5的倍数，并且不应小于2，即n≥2。为了保证规定流量特性所用的调节阀的重要弹簧，其工作圈数不应小于5，即n≥5。

通常弹簧的计算步骤如下：

1）根据工艺条件来确定当弹簧压缩到未接触时的载荷值，可以采用F₃≥1.25F₂，对于重要的弹簧采用F₃≈1.3F₂。

2）弹簧材料的选择，由使用工作条件来确定，如重要程度、工作温度等。然后决定当弹簧压缩到未接触时，相应载荷F₃时的许用应力。

3）根据表6-6，首先按载荷F₃和弹簧的中径D₁，考虑到许用应力[τ]和切应力τ之间的比值，来选择弹簧金属丝直径d。

4）按式（6-6）决定在F₃时，弹簧金属丝的实际应力。

5）由给定条件计算弹簧所需的刚度：

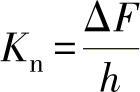
式中，ΔF载荷的增量，ΔF=F₂-F₁（N）；h为弹簧的行程，h=f₂-f₁（mm）。

6）每圈弹簧的刚度由表6-6查到，或按式（6-7）计算：

7）由比值来确定所需要的工作圈数。当n<20时，圆整为0.5的倍数；当n>20时，圆整为1的整数。

8）计算弹簧总圈数：n₁=n+2。

9）弹簧节距按式（6-8）计算：

10）当末圈为压缩和磨光时，弹簧自由状态下的长度为

H=nt+1.5d

11）为了检查弹簧在自由状态时，是否保持稳定，应满足下列条件：①当弹簧按形式Ⅰ固定时，H≤3D₁；②当弹簧按形式Ⅱ固定时，H≤5D₁。

如果上述条件不能满足，那么弹簧应靠导向套来保证末圈弹簧的方向。

12）压缩状态下的弹簧长度（末圈压缩并磨光）为

H₃=（n+1.5）d

13）弹簧的最大变形为

f₃=H-H₃

14）弹簧金属丝展开长度（不考虑工艺余量）为

L≈3.3D₁（n+2）

【例6-1】 已知F₂=800N、F₁=600N、h=30mm、D₁=80～100mm，计算设计调节阀的重要弹簧。

解 1）确定F₃。

F₃=1.3F₂=1.3×800N=1040N

2）弹簧材料选60Si2，取[τ]=750MPa。

3）由表6-6查得：弹簧的中径D₁=85mm，金属丝直径d=7mm，[τ]=τ=750MPa，载荷F₃=F=1060N，每圈的弹簧刚度K₁=37.7N/mm。当载荷降低到F₃=1040N时，弹簧应力大约减少2%。

4）弹簧必需的刚度为

5）弹簧必需的工作圈数为

取n=5.5。

6）弹簧总圈数为

n₁=n+2=5.5+2=7.5

7）弹簧螺距t为

取t=35mm，并满足条件：。

8）确定自由状态时的弹簧长度H为

H=nt+1.5d=（5.5×35+1.5×7）mm=203mm

9）验算是否保持稳定性条件：

符合保持稳定性条件。

10）压缩状态下弹簧长度H₃为

H₃=（n+1.5）d=49mm

11）弹簧最大变形为

f₃=H-H₃=（203-49）mm=154mm。

12）弹簧展开长度为

L=3.3D₁（n+2）=3.3×85（5.5+2）mm=2100mm。

3.金属膜片传动装置力的计算

在调节阀中，金属膜片最常使用于直接作用调节器的脉冲机构中。

直接作用调节器的脉冲机构如图6-9所示。脉冲阀瓣2在常开的条件下工作。当膜片4作用在顶盖3上，造成一定的压力时，这时弹簧5提高了作用力，弹簧开始压缩，同时阀瓣2在弹簧1的作用下，移向阀座的一面，其移动距离为弹簧5的挠度的大小。当挠度达到足够大时，阀瓣2就压在阀座上。因此，在脉冲式膜片-弹簧的传动装置，在调节阀中起了敏感元件和脉冲阀的传动作用，所以膜片的参数对调节器的工作影响很大。

由弹簧1和阀瓣2产生的力一般不大，可以忽略。可以认为顶盖3是在弹簧5产生的力，与膜片4上的介质压力和膜片弹性所造成力的作用下处于平衡。因此，此平衡方程式为

F_n-F_P-F_M=0

式中，F_n为弹簧产生的力；F_P为介质压力在膜片上造成的力；F_M为膜片弹性所产生的力。

为了计算方便，通常把F_P和F_M合在一起，可以用式（6-9）表示：

F_Z=F_P-F_M=pA_Z （6-9）

式中，A_Z为膜片的有效面积（mm²）。

图6-9 直接作用调节器的脉冲机构

1、5—弹簧 2—阀瓣 3—顶盖 4—膜片

为使介质压力通过膜片传动顶盖上，膜片要装得相当平整。

不论其他因素如何，按夹住周边计算的膜片直径D是不变的，并完全可以决定。因此，膜片有效面积的合理计算，是根据直径D的相当面积A来计算的，即

A_Z=φA

式中，A为按直径D计算的膜片面积，A=0.785D²；φ为有效系数。

合理的系数φ为

φ=Cφ₀

式中，C为考虑膜片行程在有效面积A_Z上（当h=0，C=1时）影响φ变化的系数；φ₀为当膜片在中间位置φ=φ₀时，考虑到其他因素对有效面积影响的初始有效系数。

在图6-9所示的结构中，通常采用平膜片和带球面支承的顶盖。膜片一般由厚度为δ=0.2mm的（厚度δ=0.1～0.3mm）06Cr19Ni10钢制造。

在试验研究的基础上，得出下列确定平金属膜片有效面积的方法。这种膜片是由直径D=25～60mm，厚度为0.1～0.3mm的06Cr19Ni10钢制造的。

初始有效系数值可按式（6-10）确定：

φ₀=0.7K_δK_dK_RK_PK_MK_n （6-10）

各系数K_δ、K_d、K_R、K_P、KM及K_n是分别考虑到膜片厚度δ₁、顶盖直径d、顶盖外表面半径R、介质压力p、材料化学成分及片数n对φ₀的影响系数，具体数值可查表6-7。

表6-7 各系数的值

系数C的计算式为

C=1±W_Ch

式中，W_C为膜片刚度系数；h为膜片行程（mm）。

“+”号用于膜片由中间位置弯向工作介质一面；“-”号用于膜片由中位置弯向弹簧一面。

膜片刚度系数值按式（6-11）确定：

W_C=0.4λ_Dλ_δλ_Mλ_pλ_n （6-11）

各系数λ_D、λ_δ、λ_M、λ_p及λ_n是分别考虑到膜片直径D、膜片厚度δ、材料化学元素质量分数、介质压力p和片数n对W_C的影响系数，具体数值见表6-8。

表6-8 各系数的值

（续）

在选择金属膜片全部行程h_n值时，推荐按表6-9进行选择。

表6-9 D与h_n的关系

在这些数值范围内，当压力不变时，膜片升高h与顶盖上力的变化关系为：当x=0，斜角的正切tanα=W_C时，为直线关系（通过点Y=Fφ₀A）。

在选择行程大小时，必须考虑到膜片使用的耐久性。

采用双层和三层膜片时，初始有效面积φ₀A值降低不大（约为6%），但是膜片刚度增加很大：由两片组成的膜片增加20%；而三片组成的膜片，比同样的单层膜片有更大的刚性，增加40%。

在带有脉冲阀的直接作用式调节阀中，膜片是传动装置，但这时膜片同样是起着根据被调液流压力变化，从而保证在活塞上压力变化的敏感元件的作用，调节器的灵敏度比脉冲机构的灵敏度要高。

脉冲机构灵敏度可由的比值来表示，即膜片行程的增量和压力增量的比值表示。因此，膜片的刚性随着行程的增加而变化，故比值就取决于所研究的膜片位置。要很快确定行程增量，是膜片在中间的位置。即时把Δh=h代入后，得出比值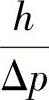，这里h为压力变化Δp值时的膜片的行程。

（1）各种因素对膜片行程大小的影响 膜片中心上升h时，顶盖（和膜片）平衡方程式为

F₁+K₁h-（F₂-K₂h）-p₁φA=0

式中，F₁、F₂为大弹簧和小弹簧所产生的力（当h=0时）；K₁、K₂为大弹簧和小弹簧的刚度；p₁为与膜片上升高度h相适应的介质压力；φ为膜片上升高度为h时的有效系数；A为按直径D计算的膜片面积。

用φ=Cφ₀代替，这里C=1-W_Ch（当膜片升高到中间位置时），同时考虑到F₁-F₂=p₀φ₀A（p₀为当h=0时的介质压力），经过适当整理后，得

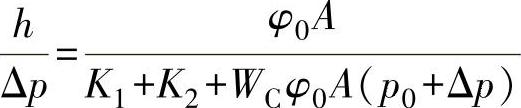
在压力增量相同时，膜片行程h随着比值的增加而增加，也就是调节阀有较大的灵敏度。因此，阀的灵敏度是随初始有效面积φ₀A的增加（不成比例）及弹簧刚性K₁、K₂和膜片刚度W_C的减小而增加。但是在这种情况下，应注意弹簧力随着初始有效面积的增加而增加，因此这种变化与弹簧刚度有关。

如果K₂和K₁比较，Δp和p₀比较，K₂和Δp都可以忽略的话，得

因此，膜片传动的灵敏度，取决于和W_Cp₀两个值的总量。从前者可以看出，有效面积的增加，又有当它们不能与弹簧刚度K₁的增量成比例时，才是合理的。同样，为了增加灵敏度，就应合理减小膜片刚度系数W_C。在其他条件相同的情况下，随p₀的增加，膜片传动的灵敏度降低。

（2）膜片直径D对膜片传动装置灵敏度的影响 如果弹簧圈数不变，同时弹簧中径和膜片的直径是成比例的。当φ₀不变时，膜片有效面积与膜片直径成D²的关系。当膜片直径增加n倍时，为了平衡介质作用力，弹簧作用力必须增加n²倍。弹簧作用力F可用式（6-12）计算：

式中，C₀为总系数；d为金属丝直径；D₁为弹簧中径。

在直径D₁增加n倍时，为使弹簧力增加n²倍，金属丝的直径必须增加n倍。在这种情况下，每圈弹簧的刚度也增加n倍。因此，可用下式表示：

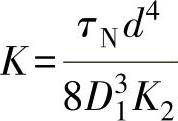
式中，τ_N为剪切系数；K₂为系数，其值见表6-2。

因此，膜片直径增加n倍时，弹簧刚度也增加n倍，而有效面积增加n²倍，故比值减小n倍。由此可见，随着膜片直径的增加，膜片装置灵敏度也增加。

（3）弹簧刚度和膜片刚度的关系 对于膜片传动装置和工作压力为p₂=20.0MPa，脉冲机构“阀前”式压力直接作用调节阀，当d/D=0.97时，由3层厚度为δ=0.2mm制成的膜片调节装置，膜片直径为D=30mm，顶盖球面半径R₂=90mm，大弹簧刚度K₁=333N/mm。这种情况下为

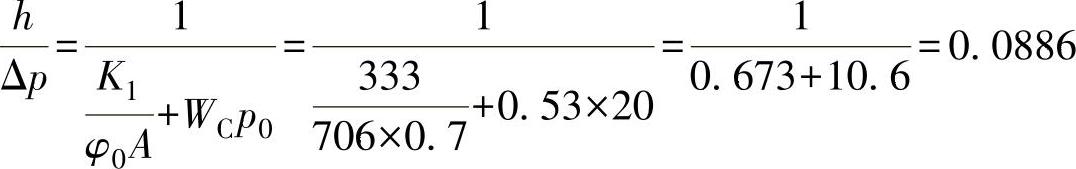
这里取A=706mm²、φ₀=0.7、W_C=0.53。因此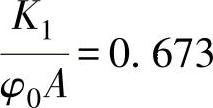，，而W_Cp₀=10.6。从数值上可以看出，膜片刚度是有决定影响的，而弹簧刚度影响不大，大约是膜片刚度的6.5%。因此，W_Cp₀是应特别注意的。

下面再来研究压力为PN10时，计算调节阀的情况。调节阀膜片直径D=60mm（A=2827mm²），顶盖直径d=44mm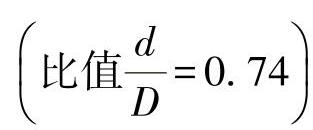，，大弹簧的刚度K₁=123N/mm。当膜片厚度δ=0.2mm时，取φ₀=0.77、W_C=0.26，代入后得

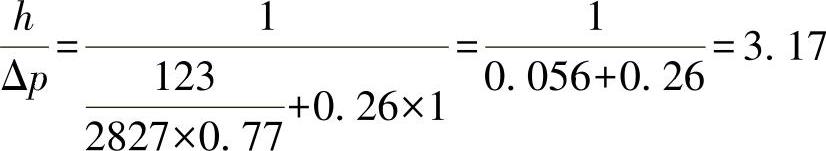
因此，在所研究的两种结构中，膜片刚度比弹簧刚度大，但在第一种情况下，当膜片直径D=30mm、压力p=20.0MPa时，膜片刚度比弹簧刚度约大16倍。在第二种情况下，当膜片直径D=60mm、压力p=1.0MPa时，膜片刚度比弹簧刚度约大4.6倍。

由上述分析得出，为提高膜片传动装置的灵敏度，首先应保证膜片有小的刚度（增加膜片直径，减小厚度，采用柔软材料等），同时降低弹簧刚度（增加圈数和弹簧中径等）。但对于刚性膜片不可能有好的效果。

引用已得的数据，可以确定造成膜片行程所需的压力的增量（绝对值和相对值）。

平面金属膜片的弹簧-膜片传动装置的脉冲阀上升高度为

或近似为

在所研究的两种情况中，按近似值来确定也比较正确。对第一种情况，h=Δp/11.3；对第二种情况，h=Δp/0.316。

如果膜片行程在二种情况中都取h=0.2mm，那么在第一种调节阀中，要求压力变化为Δp=11.3h=11.3×0.2MPa=2.26MPa。在第二种调节阀中，Δp=0.316h=0.316×0.2MPa=0.063MPa。对第一种调节阀，当p₀=20.0MPa时，Δp为11.3%；对第二种调节阀，当p₀=1.0MPa时，Δp为6.3%。