调节阀的工作流量特性曲线,可用阀瓣的位移与介质流量的关系确定。通常表示为
qm=f(h)
已知这种关系,便可计算阀瓣在与其开启高度h相应的各种位置下,阀门所要求的通过能力qmk。
按通过能力qmk,或公称通过能力qmyk的大小,确定阀瓣在不同位置时阀座的开启截面积Ak。阀瓣尺寸的计算和绘制,根据Ak值进行。下面介绍一些已采用的计算方法。
1.阀瓣开启截面积的计算阀门的流量qmk可以绝对值计算(t/h)。但流量往往不以绝对值表示,而以相对值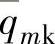 (与在调节范围内的最大流量qmmax的比值)计算,并要求流量按一定的曲线图变化。
(与在调节范围内的最大流量qmmax的比值)计算,并要求流量按一定的曲线图变化。
在这种情况下,将阀瓣在各种不同位置下阀座的开启截面积Ak,折算成阀门通道孔面积Ay的比值计算起来更方便些。阀瓣全开时,其开启截面的最大面积为
Aσ=mAy (3-112)
式中,m为全通过系数,m≤1。
系数m表示阀瓣在全开启时,阀座开启截面积与通道孔面积的比值。m=1的阀门通常称为“全通阀”。
Ak值可用阻力系数ζk、总流量系数KVk、阀座的流量系数KVb,以及按公称通过能力qmyk(或者流量系数KV)进行计算。这些数值是相互关联的,采用其中每一数值都各有其特点。在利用这些系数值的试验数据时,应将所依据的截面积和其相应的介质流速考虑在内。
当流量的绝对值为已知数时,阀座开启截面积借助阻力系数ζk,用下列方法求算。
利用关系式qmk=f(hk),即流量值与阀瓣开启高度的关系式,确定阀瓣在不同开启位置下的必须值qmk。qmk与相应的ζk关系为

式中,Δp值应给定,或者由qmk的值确定。如缺乏必要的数据,为了近似计算,一般在一定条件下,取Δp=常数。令 。
。 为以相对值表示的阀门开启截面积。当Ak=Ay时,
为以相对值表示的阀门开启截面积。当Ak=Ay时, 。
。
利用所给定阀门的形式和尺寸的关系式 求出与给定的ζk值相应的阀的必需开启度
求出与给定的ζk值相应的阀的必需开启度 。然后由式(3-114)确定阀座的开启截面积Ak:
。然后由式(3-114)确定阀座的开启截面积Ak:

对于双座式调节阀,其关系式为 的曲线如图3-118所示。
的曲线如图3-118所示。
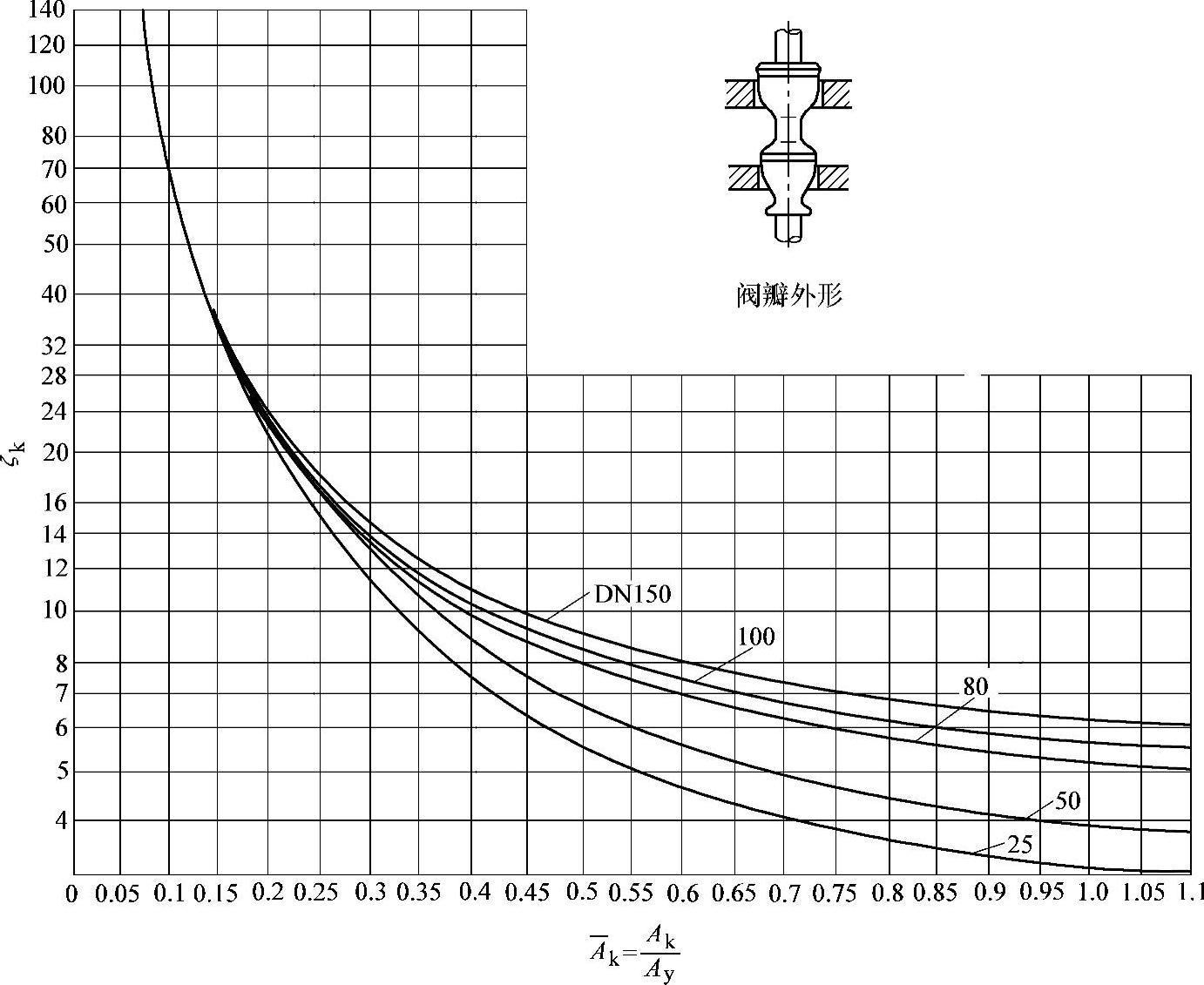
图3-118 双座式调节阀因开启高度而变化的流体阻力系数曲线图
研究证明,阀瓣在给定开启位置时,阀门的阻力系数ζk基本上决定了阀的开启度。开启度决定于阀体形状,而阀瓣形面的变化Ak则影响很少。因此,曲线图可用于计算各种不同阀瓣形面调节阀的阻力系数。按给定的阀体阻力系数选用曲线。
如果流量的绝对值为未知数,但可以曲线图或公式形式绘出相对值qmk,则阀座的开启截面积按下列程序进行计算。
知道阀体的结构尺寸后,就给定了与(在调节行程范围内)阀的最大开启度相应的阻力系数值ζM。确定ζk和ζM之间的关系式,并计算阀瓣在不同位置下的ζk值。利用ζk=Θ 曲线图,确定与求出的ζk相应的
曲线图,确定与求出的ζk相应的 值。
值。
下面列举在恒定压力损失下,按流量值计算开启截面积的例题。
【例3-2】 在全开启时,阀门的阻力系数ζM=8.0,试求DN80的直线特性曲线的双座式调节阀阀座的开启截面积。
解 所考虑的阀门的阀瓣为直线特性曲线。由此得出关系式为

将阀瓣的全行程hn分成n个部分,并用字母k代表所研究的与阀瓣开启高度hk相应各截面的序号,阀瓣的行程以相对值表示:

因为 和
和
故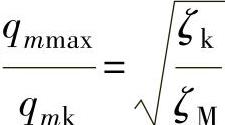 或
或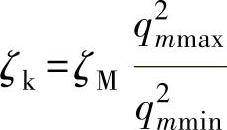
但是 
因而对于直线特性曲线,有
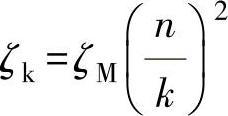
取n=10,并将k的不同值代入此公式,得出阀瓣在每一开启位置下的ζk值。利用图3-118的曲线图,确定相应于ζk值的开度 。
。
计算阀座的开启截面积。对于所研究的阀而言
Ay=0.785×82cm2=50.27cm2
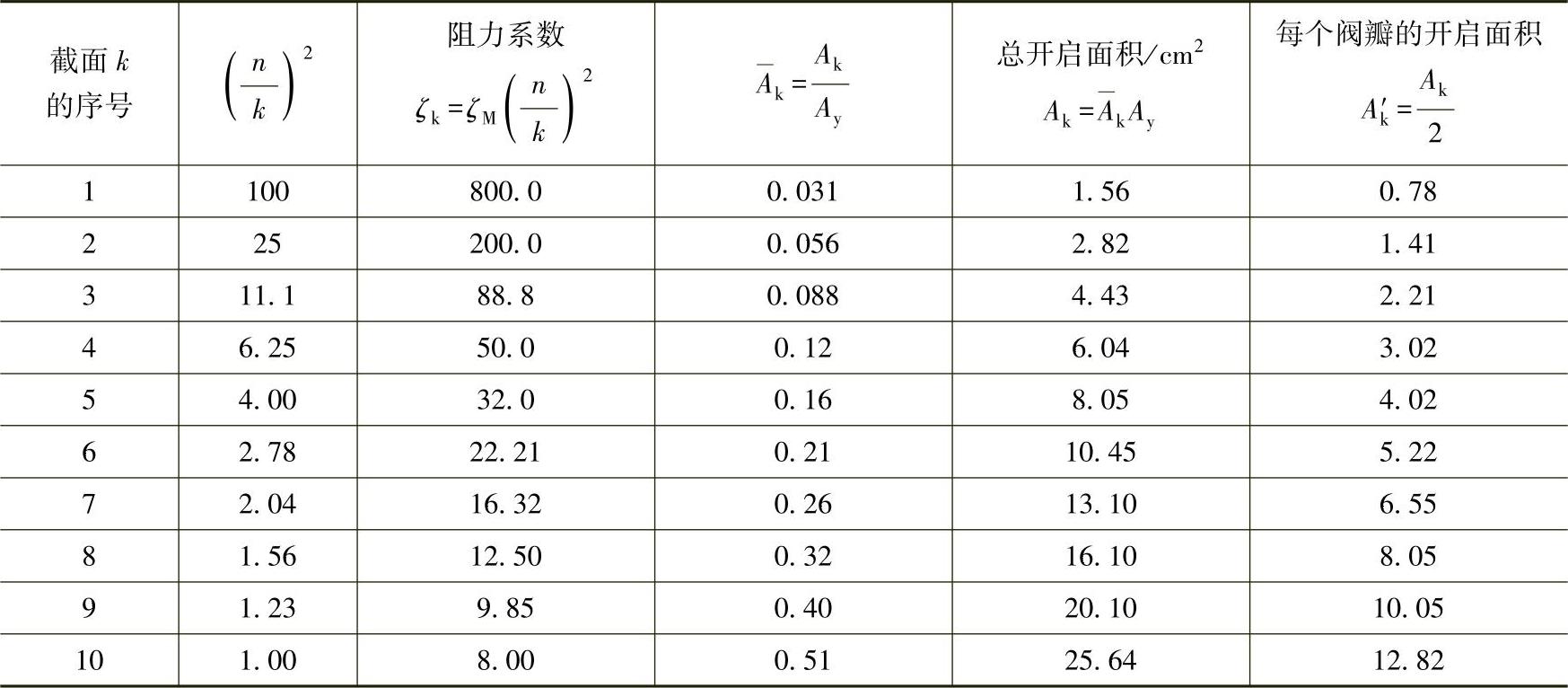
计算数据见表3-46。
表3-46 数值 、ζk、
、ζk、 、Ak和Ak′的计算值
、Ak和Ak′的计算值
用总流量系数KVk确定阀座的开启截面积Ak,可按绝对值计算,也可按相对值计算。在未研究计算方法之前,应明确什么是总流量系数KVk。
由水力学的定律得知,在无阻力的管子里,液体的理论流速vt(m/s)为

由于存在阻力的缘故,实际流速值要小些,为

式中,ζ为管子的阻力系数,这里指包括阀门在内的整个管路系统的阻力系数。
因此,有 vδ=φvT
其中 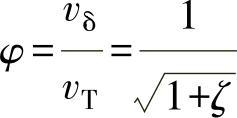
式中,φ为流速系数,是实际流速与理论流速的比值。
φ值仅与ζ值有关。为了求生实际流速(以及流量)和阀的开启截面积之间的关系,用经验数据或者由ζ值中推导出如下关系式:

式中,KVb为阀座的流量系数,即与管道中的介质流速有关的阀门的开启截面的流量系数。故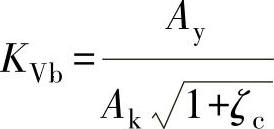
计算整个系统(包括阀在内)的阻力系数ζc,其总和为
ζc=ζT+ζk
式中,ζT为没有阀门的系统阻力系数;ζk为在给定开度下调节阀的阻力系数。故
假如系统的阻力与调节阀的阻力相比,小到可以忽略而不计,则取KVb=KVbk,得(设ζT=0)

因而 
由此可见,流量系数KVbk不仅决定于调节阀在其给定的开度下的阻力,而且决定于管路的阻力。
在某些场合下,设计计算调节阀时,不可能有安装该调节阀那个系统的阻力方面的数据。例如,绝大多数调节阀,作为在各种不同条件下使用的通用工业阀门,在设计调节阀时,通常假定ζT=0。
这样假定,虽然使设计稍许带有近似性,但并未使其超出现实条件的范围。因为正常使用时,实际压头的相当大的一部分总是调节阀本身形成的。换言之,有调节阀的阻力,总比不带调节阀的系统阻力高。
阀门的阻力系数为
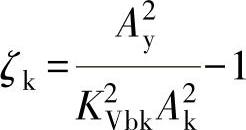
将其代入流量公式,则得

当阀的开度很小时,此算式的分母接近于1,例如,当 时,它等于0.99。所以
时,它等于0.99。所以
当阀的开启度很小时,取分母为1,流量可按上述的公式计算。
取 
式中,KVk称之为总流量系数,由此

此公式在计算阀门流量时经常用到,并且,所采用的KVk值用预先以试验方获得。
根据试验数据计算KVk值,应按下式进行:
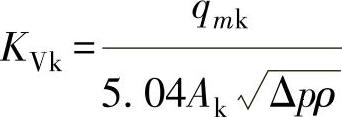
上式说明,确定流量系数的试验公式,应该与采用此流量系数的公式一致。
因为 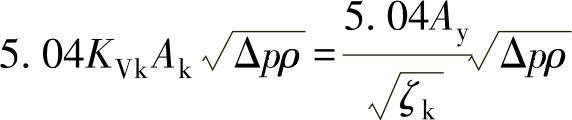
则 
因此,当给定开启截面积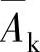 时,总流量系数取决于阀的开启截面积
时,总流量系数取决于阀的开启截面积 和阻力系数。
和阻力系数。
影响阻力系数ζk值的不但有 ,而且还有阀的流道形状和尺寸:并且随着阀的开启度增加,后一因素的影响愈显著。
,而且还有阀的流道形状和尺寸:并且随着阀的开启度增加,后一因素的影响愈显著。
按流量qmk的绝对值,确定阀座的开启截面积Ak时,用总流量系数按照下列程序进行计算。
用流量值与阀瓣开启高度的关系式,来确定阀瓣在各种不同开启位置下的流量。
对qmk的每一数值,应计算由KVkAk乘积所定的必需的“有效质量流量”,即

因此,要确定KVk和Ak值的相互关系是有一定困难的。确定Ak值有试凑法和古特金逐步渐近法两种方法。
试凑法,按Ak乘积,用试凑法得出所需的值。这时要利用总流量系数与阀开启度的关系式曲线:

采用古特金逐步渐近法时,需预先作KVk=φ(KVkAk)曲线。
按流量qmk的相对值计算阀座的开启截面积Ak时,用总流量系数KVk进行计算。计算程序与按流量的绝对值计算相同。由于按流量的相对值计算较常见,故把它推导成下面的较简便的形式。它适用于具有直线特性曲线的阀瓣。
对于具有直线内特性曲线的阀瓣,设通过调节阀的最大流量为
qmmax=qmAKVkmAy
其中 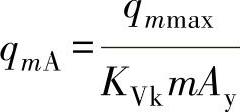
式中,qmA为当阀瓣全开时,介质流经单位有效面积的流量;KVk为阀瓣全部开启时的总流量系数。
阀瓣为直线特性曲线时,如果qmmin=0,则

如果qmmin≠0,则

代入qmmax值,得

对于处于中间位置的阀瓣为
qmk=qmAKVkAk
使上面qmk两式值相等,得
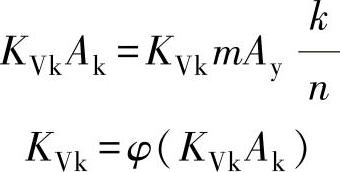
用试凑法或按曲线确定Ak值;然后根据Ak值,由KVkAk乘积求出所要求的KVk值。
【例3-3】计算DN50,阀瓣为直线特性曲线的单座式调节阀,在全通系数m=1时(即全通阀)阀座的开启截面积。阀瓣行程hn=65mm。最小流量qmmin=0。
解 确定通道孔面积:
Ay=0.785×52cm2=19.63cm2
因为未给出流量的绝对值,利用图3-119所示的数据,本例应选用最下面一条曲线;按此曲线确定所需要的数值。
当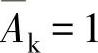 时,KVk=0.42。
时,KVk=0.42。
用已知的数据代入,得

将k值依次代入,得出“有效质量流量”的KVkAk值,由此以试凑法确定阀座的开启截面积Ak。选出Ak值,由KVkAk乘积,得出所要求的数值。以一系列逐步渐近的方法进行计算,直至KVk的最后两位数值不等为止。计算数据列于表3-47。
采用这种逐步渐近法是必要的,因为当乘积KVkAk为给定值时,其相乘数可能有几个数值,而且相乘数的本身值之间与图3-119所示的关系有关联。

图3-119 一些单座式调节阀选用的总流量系数值曲线图
对于不同的阀,由于阀瓣和阀体的结构不同,在 值相同时,总流量系数会稍有差异。
值相同时,总流量系数会稍有差异。
图3-120a所示的双座柱塞式调节阀,在 的直线特性曲线情况下,其KVk值可按下面近似公式求出:
的直线特性曲线情况下,其KVk值可按下面近似公式求出:

表3-47 利用总流量系数KV的近似法计算单座式调节阀阀座开启面积

如前所述,按 曲线图,根据
曲线图,根据 值,绘出
值,绘出 ,或者
,或者
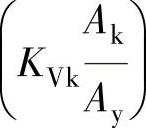 曲线图。借此曲线图,用图解法可求出KVk值。KVkAk值单位为cm2。为了得出KVkAk值,对于不同的DN,可沿横坐标轴取Ak值的相对值
曲线图。借此曲线图,用图解法可求出KVk值。KVkAk值单位为cm2。为了得出KVkAk值,对于不同的DN,可沿横坐标轴取Ak值的相对值 。
。
图3-121a为KVk-Ak曲线,根据KVk=φ(Ak)数据,可绘出KVk=φ(AvAk)曲线。
因此,在用图解法求KVk时,绘制出的第二种曲线图(图3-121b),可代替编制近似表格。用曲线图根据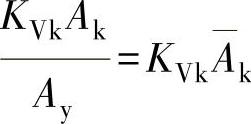 确定KVk值。知道KVk值就可求出Ak值。
确定KVk值。知道KVk值就可求出Ak值。

图3-120 调节阀
a)柱塞式阀瓣 b)空心窗式阀瓣

图3-121 DN25单座式调节阀的曲线图
a)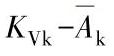 曲线图 b)
曲线图 b) 曲线图
曲线图
由于积累了试验数据,用不同形式调节阀的公称通过能力的曲线图 ,确定Ak值的方法,在最近得到应用。此时,可用以下方法确定Ak值。
,确定Ak值的方法,在最近得到应用。此时,可用以下方法确定Ak值。
首先确定与阀瓣内特性曲线相对应的阀瓣处于各种位置的qmk值;然后确定公称通过能力:

利用与阀门结构相对应的每一DN的 曲线图,可得出每一qmk值的
曲线图,可得出每一qmk值的 值。阀瓣的截面积可用式(3-116)求得
值。阀瓣的截面积可用式(3-116)求得

用阻力系数ζk、总流量系数KVm或公称通过能力qmyk,可以计算调节阀的阀瓣。阀瓣预先经过试验,并给出与它所相应的曲线图。
对于新型调节阀的阀瓣,应参照与所设计的阀相近似的结构,采用某一调节阀的曲线图来代替所设计的,然后只能近似地给出其型面。
ζk、KVk和qmyk取决于阀体阻力与阀座缩口的阻力。这些数值的单个作用不显著,可以按其总和计算,并把ζk和KVk的变化,看作是因Ak改变所致。
调节阀的阻力在一定条件下(具有一定的近似性),可认为由三部分组成,如图3-122所示。截面A—A、B—B表示阀座前与阀座后的阀体阻力;截面C—C表示用阀瓣调节阀座孔的阻力。
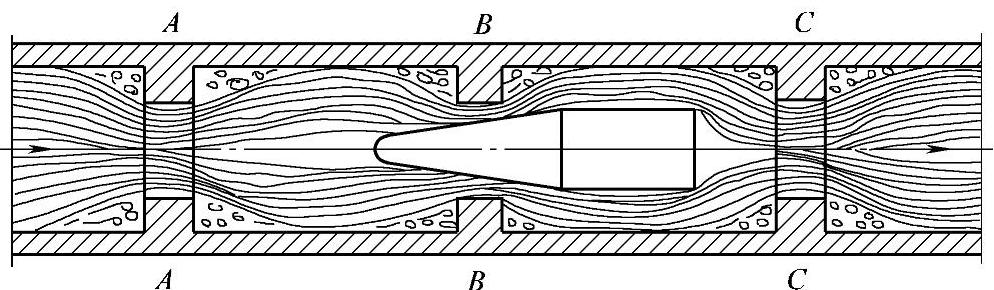
图3-122 调节阀阻力示意图
总阻力系数为
ζk=ζⅠ+ζⅡ+ζⅢ
式中,ζa为阀体的阻力系数,ζa=ζⅠ+ζⅢ;ζb为阀瓣的阻力系数,ζb=ζⅡ。
ζk=ζa+ζb
阻力系数与截面Ay的介质流速有关。
现将图3-123所示的几个阀体不同的阀门阻力系数进行对比。
 曲线图,可将其分成相当于ζa和ζb的两个部分,则(图3-123c)
曲线图,可将其分成相当于ζa和ζb的两个部分,则(图3-123c)
Δp=Δpa+Δpb
此时,阻力系数曲线将具有下列特点:曲线图上部(相当于ζb值)相同,而曲线图下部(相当于ζa值)则不同,因此,由
 值,完全可以定出ζb值。此值不决定于阀体,而且在阀瓣的结构相同时,对于所研究过的几种调节阀全都一样。这样虽然不能认为绝对准确,但在实际应用上已具有足够的准确度。从理论上讲,ζa和ζb可能相互影响,但ζa对ζb的影响程度很小,在一般计算中可忽略不计。
值,完全可以定出ζb值。此值不决定于阀体,而且在阀瓣的结构相同时,对于所研究过的几种调节阀全都一样。这样虽然不能认为绝对准确,但在实际应用上已具有足够的准确度。从理论上讲,ζa和ζb可能相互影响,但ζa对ζb的影响程度很小,在一般计算中可忽略不计。
如果Δp=常数,则Δpa和Δpb的变化曲线形状将如图3-123d所示。
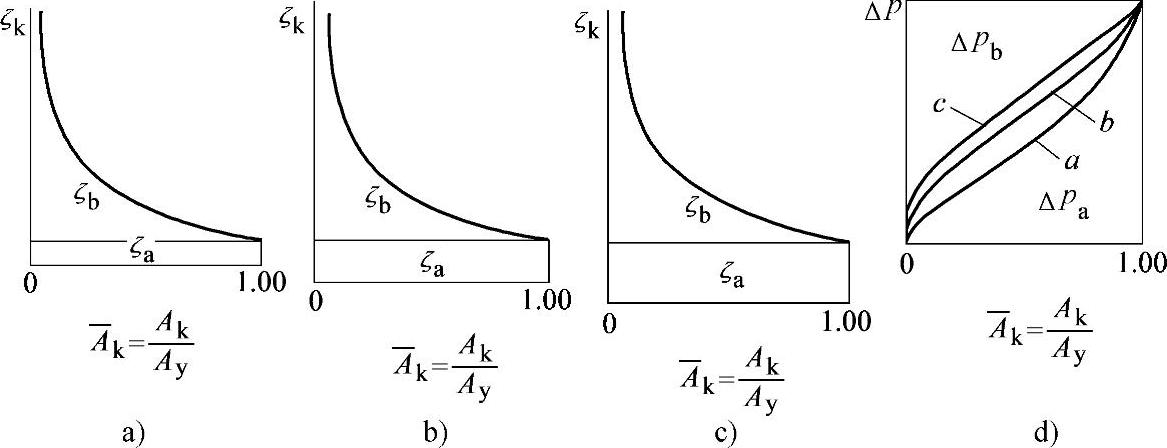
图3-123 在阀体的不同阻力系数ζa及与其相应的阀体压力损失为Δpa、阀瓣压力损失为Δpb时,调节阀阀瓣开启时的阻力系数变化示意图
借助阀座的流量系数KVb,利用下式确定阀座的开启截面积Ak

此式与式(3-115)相似,但其中阀座流量系数KVb仅与阀座阻力有关,即

由式(3-117)得
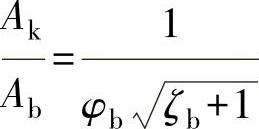
图3-124示出双座和单座式调节阀的阀座流量系数曲线图。

图3-124 阀座流量系数曲线图
1—双座式调节阀(ζbmin=0.8~1.0) 2—DN50和DN65单座式调节阀(ζbmin=1.0)
用这种方法计算,比按总流量系数KVk的计算方法要简单些,因为KVb值的变化范围比较小。
计算调节阀时应注意,为了使调节工作满意,必须使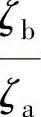 值不要过分小。建议取
值不要过分小。建议取 。若此条件达不到,则阀瓣对水流的作用将过分小。
。若此条件达不到,则阀瓣对水流的作用将过分小。
实际上ζb=0时,阀瓣的位移不会使调节阀的阻力增大,因而不能改变介质的流量。
设计调节阀阀体时,最好能保证阀体的阻力小些。为此,应尽可能使阀体内腔的通道截面尺寸相等,并接近Ay值。
以上叙述了确定Ak值的几种方法。具体选用哪种方法,视已知数据如何而定。最简单的计算方法是采用qmyk法,其次是采用KVk法。
2.阀瓣的形面绘制
利用表格或曲线图所示的阀瓣,在不同开启位置下的开启面积Ak来绘制阀瓣的形面。对于各种类型的阀瓣,其形面绘制方法各异。
(1)柱塞形阀瓣 首先研究用柱塞形阀瓣调节液流时,介质的流动情况。
在不同时刻,相对于阀座而言,阀瓣处于不同的开启位置,与开启截面积有关的介质流量也就大小不同。在绘制阀瓣形面时,其任务是根据所计算出的数值,来规定与阀瓣各截面相应的开启截面积的尺寸。
偶然看(图3-125),似乎在A—A平面上的阀瓣与阀座之间的环形截面积,是起限制作用的面积。但此截面完全不是最窄的截面,而且它并不能限制介质通过。比较正确的见解是:起限制作用的面积Ak,是截锥体MNN1M1的侧表面面积。此截锥体的母线MN是位于阀座上的靠近于阀瓣的一点,至阀瓣侧面的垂直线。但这种说法也不能确切地说明此问题。

图3-125 流体在阀瓣与阀座之间流动示意图
采用使用有侧表面为等值面积的截锥体所形成的曲线,来绘制阀瓣形面的方法,所得出的结果最正确。为了简便起见,以后把这些曲线简称为等值面积曲线。
如图3-126所示,当给定阀瓣位置时,保证开启截面积Ak,就意味着要创造这样的条件,即介质通过最狭窄处的面积等于Ak。
自M点以各种不同角度α引若干射线,假如这些射线为锥体的母线,且锥体的侧表面面积等于Ak,则在这些射线上,可得出截距MC1、MC2、MC3等。

图3-126 按x和y坐标系绘制等值面积曲线示意图
连接C1、C2、C3等点,得出其值等于Ak的侧表面积的截锥体母线。流束在阀瓣与阀座之间通过时,将绕过M点。因此在阀瓣与阀座间,间隙最狭窄处向下的一段,所绘制的阀瓣形面,应该与等值面积母线的曲线相交,母线上的一点(限制的),应与阀瓣的形面重合,而且此形面在此点与等值面积的曲线相切。
等值面积母线曲线可按照下列数据绘制:截锥体侧表面面积应等于阀瓣开启截面积,即

式中,l为母线长度,在所研究的场合,l=MC;D为下遮盖直径,在所研究的场合,D=Dc;d为上遮盖直径,d=Dc-2lcosα。将这些数值代入,得
Ak=πlDc-πl2cosα
为了绘制等值面积母线曲线,确定以M点为坐标原点,则

因此,有 
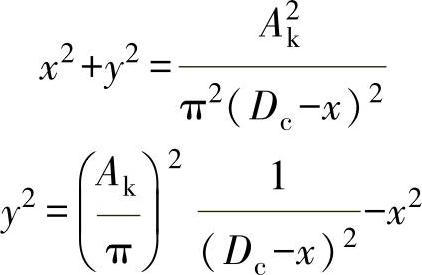
利用后一方程来绘制图3-126所示的等值面积曲线,用x和R坐标绘制等值面积曲线。x为横坐标,R为距计算原点的距离,如图3-127所示。绘制时,在横坐标x上作垂线,并在原点上以R为半径,截取高度。

由于流量系数随开启截面积的改变而变化,所以等值面积母线可能这样分布,即其中有一根曲线越出公用包络线,也就是说不可能绘制出全部等值面积曲线的公用包络线。当阀瓣的全行程hn不够时将产生这种现象。

图3-127 按x和R坐标绘制的等面积曲线图
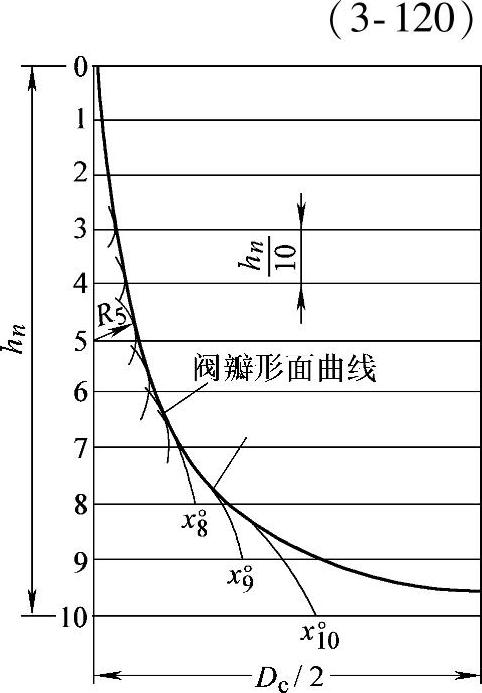
图3-128 等值面积曲线与圆弧曲线的交界区分布

图3-129 阀瓣形面的形成示意图
为了保证绘制公用包络线的可能,必须满足式(3-120):
hn≥n{y(i-1)[x°(i-2)]-yi[x°(i-2)]}式中,y(i-1)[x°(i-2)]为当位于序号i-2曲线上横坐标等于x°时,在序号i-1曲线上的纵坐标;yi[x°(i-2)]为当位于序号i-2曲线上的横坐标为x°时,序号i曲线上的纵坐标。
照例,在校验是否满足给定条件时,通常需要这些曲线中的最后几根曲线。如果是绘制阀瓣形面曲线,通常取10个截面已足够了(图3-128),则

式中,Ac为阀座孔面积;x8°为第8段的横坐标(图3-128);A8、A9、A10为当 、0.9、1.0时,阀瓣的开启截面积。
、0.9、1.0时,阀瓣的开启截面积。
以上述资料为基础,按以下步骤绘制阀瓣的形面(图3-129):
1)选定绘制阀瓣形面的比例(通常为10∶1),并引出阀瓣的纵坐标轴,在轴的两侧再以相当于 的距离绘出两条线(按选定的比例)。
的距离绘出两条线(按选定的比例)。
2)量取阀瓣行程,并将它划分成n等分。
3)求出1~10截面每一截面的Ak值。
4)绘出每一截面的等值面积母线的曲线。
5)划出已绘出的曲线的包络线。
阀瓣的最下部分的外形轮廓可任意做出。但是阀瓣的形面任何地方也不应相交于以Ak=mAy绘出的等值面积母线的曲线。
为了简化计算程序,对于 (y°为x=0时的纵坐标;x°为y=0时的横坐标),可用圆弧代替曲线。这对于实际应用,精确度已足够了。
(y°为x=0时的纵坐标;x°为y=0时的横坐标),可用圆弧代替曲线。这对于实际应用,精确度已足够了。
定出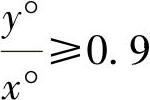 的截面的初步数目后,可以不绘制这些曲线。
的截面的初步数目后,可以不绘制这些曲线。
因为
 (https://www.xing528.com)
(https://www.xing528.com)
则当x=0时
当y=0时
利用形面的一侧,得

根据求出的数据列出不等式:

经适当整理后,得
Ak≤0.09πD2c 或 Ak≤0.36Ac
其中 Ac=0.785D2c
因此,对于 截面的
截面的 等值面积曲线,可以以圆弧代替。
等值面积曲线,可以以圆弧代替。
阀瓣形面的绘制如图3-129所示。
【例3-4】绘制DN50,调节行程hn=65mm,具有直线特性的单座式调节阀阀瓣的型面。阀的压力损失恒定。Ak值参照表3-47的数据。
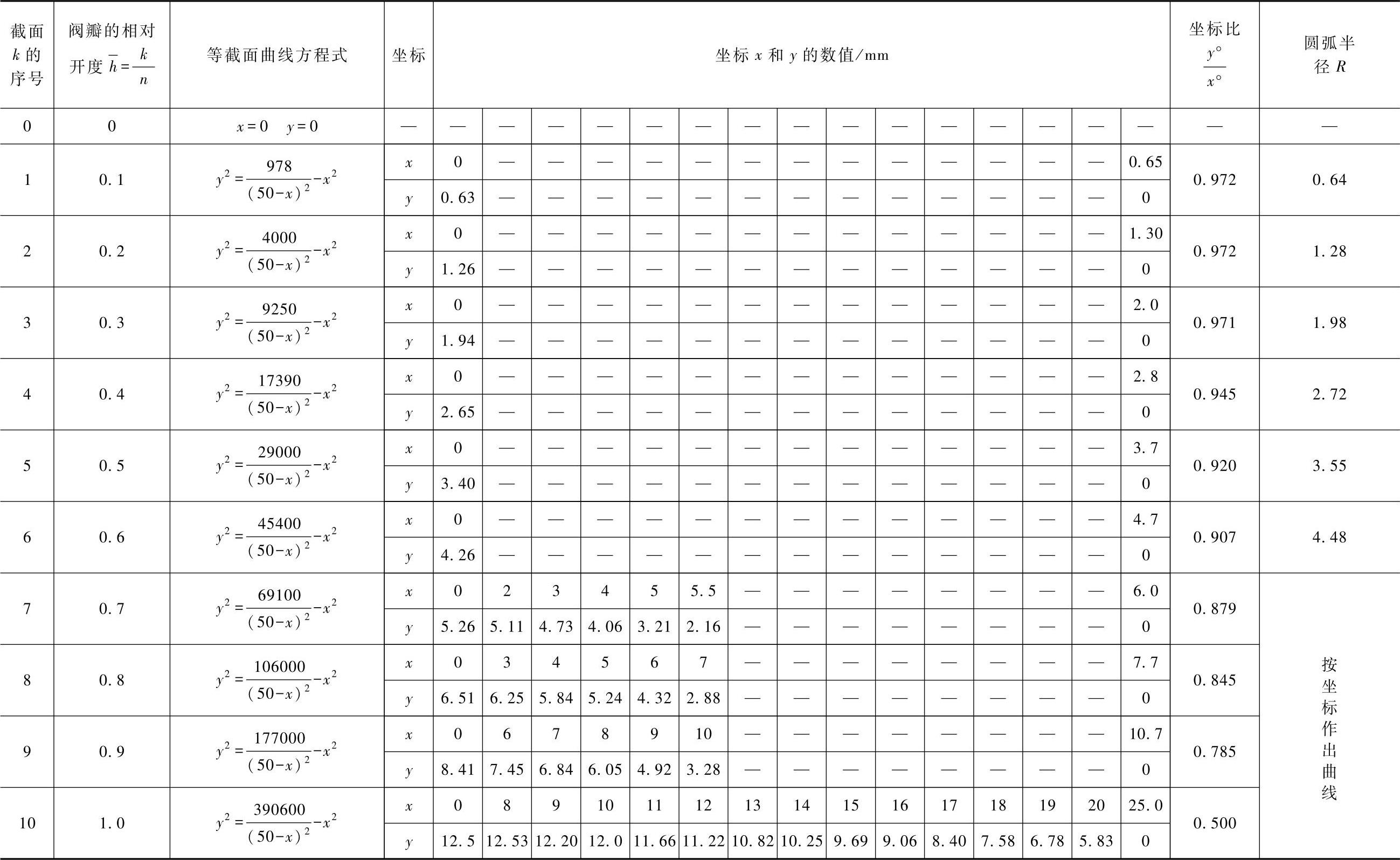
解 计算10个截面,得出每一截面的等值面积曲线方程的计算值。方法是将与该截面相应的Ak值代入式内。
用两种方法解这个问题。
1)直角坐标系法:

列出的方程计算每一截面x°在y=0时的x值;截面y°在x=0时的y值。对于那些曲线形状接近于圆弧的截面不绘制曲线,而绘制半径为 的圆弧。这种做法适用于
的圆弧。这种做法适用于 的截面(表3-48,截面自
的截面(表3-48,截面自 至
至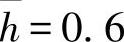 )。此方案通常用于截面Ak≤0.36Ac的场合。
)。此方案通常用于截面Ak≤0.36Ac的场合。
表3-48 在直角坐标系中用于绘制阀瓣形面的计算数据
绘制曲线可以限制在曲线与阀瓣形面预计切点附近的线段,如图3-130所示。
2)x与R坐标系法:

对于Ak≤0.36Ac的截面,其公式改为

计算结果列于表3-49。绘制曲线限于x°k-1到x°k的范围(x°k为当y=0时的横坐标)。
x°k值按式(3-121)求得

阀瓣的形面是绘制出的全部曲线和圆弧的包络线。包络线一般用图解法绘制,也可以用解析法计算。由于解析法比较复杂,在实际应用中不采用。
前面已指出,阀瓣最下面部分的外形轮廓可以任意做出,然而阀瓣形面的任何部位,都不应与A10的等值面积曲线相交。

图3-130 柱塞形阀瓣形面的绘制
阀瓣形面绘出后,再计算标注在阀瓣施工图上每一截面的直径。
首先确定阀瓣上部(其母线为直线)的锥形段,然后确定锥形段下面的异形段。在图上标注多少截面数目,与所要求的形面精确度及曲率有关。
为了将异形段形面曲线修正圆滑,应当将等距截面前一段的阀瓣直径增大,后一段减小。
阀瓣的最终尺寸最好在实验室内,或者在阀的实际工作条件下用试验方法进行修正,以使其更为精确。
(2)空心窗形阀瓣 在空心窗形阀瓣内,介质通过阀瓣套筒壁上的窗口所形成的截面。空心阀瓣的窗口可以是方形或异形。
异形窗口的形面按下列程序进行绘制:
首先作业以直线线段组成的近似的形面,然后绘制出窗口的最终形面的曲线,如图3-131所示。
近似形面按下列公式进绘制:

式中,lk为所要求的截面内的窗口宽度(cm);lk-1为前一截面内的窗的宽度(cm);Ak为所计算截面内阀瓣窗口的开启面积(cm2);Ak-1为前一截面内的窗口开启面积(cm2);h为截面之间的距离(cm);z为窗口数目。
当流量系数变化平缓时,面积Ak-Ak-1也逐渐增加,比较容易用圆滑曲线直接绘制近似形面。当流量系数按复杂曲线变化时,截面Ak-Ak-1的变化很大,所得到的形面与齿形相似。在这种情况下,必须增加复杂曲线段的截面数目,以减小h值。
初始形面可用矩形法绘制(图3-131b)。此时,有

表3-49 在x和ρ坐标系中用于绘制阀瓣形面的计算数据

型面作图的精确度,在很大程度上取决于计算截面的数目。因此建议计算截面尽可能选得多一些。把型面的下部截面数目划分得多些尤为重要。
【例3-5】 试确定轴流式套筒调节阀的套筒钻孔直径、数量及排列方式。
已知:调节阀的形式为轴流式套筒钻孔阀;公称压力和公称尺寸为Class600、DN250,Class900、DN300;环境温度为-40~60℃;入口介质温度为0~60℃;介质为天然气,p(CH4)=96.226%,M≈16.04。介质参数如下:

图3-131 空心窗形阀瓣形面的绘制
a)梯形法 b)矩形法
气体常数R=518kJ/kg;密度ρ=0.7174kg/m3;相对密度(空气=1)=0.5548;熔点=-182.5℃;沸点=-161.49℃;定压比热cp=1.545kJ/Nm3;绝热指数K=1.369;临界压力p0=4.641MPa;临界温度T0=190.7K;临界比容U0=0.0995m3/kmol;临界压缩系数Z0=0.290;热导率λ=0.084W/(m·℃);动力黏度μ=10.395×10-6Pa·s;运动黏度ν=14.50×10-6m2/s。
流量特性为等百分比或近似等百分比。
流量对于Class600、DN250,qVmax=70×104m3/h,qVmin=9×104m3/h;对于Class900、DN300,qVmax=90×104m3/h,qVmin=10×104m3/h。入口压力:对于Class600、DN250,p入=10.0MPa;对于Class900、DN300,p入=12.0MPa。出口压力:对于Class600、DN250,p出=4.0MPa;对于Class900、DN300,p出=4.0MPa。阀门开度为15%~85%。精度为±1.0%。回差≤1.0%。流量必须以最大流量110%为基础。流过阀内件的速度头低于480kPa。阀芯出口流速<68m/s。出口处流速≤40m/s。噪声:距阀门1m处不得超过85dB。泄漏等级为IEC60534-4:2006中Ⅳ级。流体方向为流关。
解:1)首先把标准流计算成工况流量。
①对Class600、DN250,有
qVp,max=70×104m3/h/100+1=700000m3/h/101=6930.69m3/h
qVp,min=9×104m3/h/100+1=90000m3/h/101=891.09m3/h
②对Class900、DN300,有
qVp,max=90×104m3/h/120+1=900000m3/h/121=7438.02m3/h
qVp,min=10×104m3/h/120+1=100000m3/h/121=826.446m3/h
2)设计工况流量。
①对Class600、DN250,有
6930.69×110%m3/h=7623.759m3/h
②对Class900、DN300,有
7438.02×110%m3/h=8181.822m3/h
3)判断是否为阻塞流。
对于气体当X≥FγXT时为阻塞流,当X<FγXT时为非阻塞流。
①对Class600、DN250,有
X=Δp/p1=p1-p2/p1=(10-4)/10.1=0.594
查标准GB/T 17213.2—2005,得
CH4:γ=1.32、Fγ=0.943、XT=0.68。
则 
FγXT=0.641
于是X<FγXT,流态是非阻塞流。
②对Class900、DN300,有
X=Δp/p1=8.0/12.1=0.66116

FγXT=0.942857142×0.68=0.6411
故X>FγXT,流态是阻塞流。
4)计算流量系数C。
①对Class600、DN250,流态是非阻塞流。


②对Class900、DN300,流态是阻塞流。


5)计算调节阀雷诺数。
① 
对Class600、DN250,有
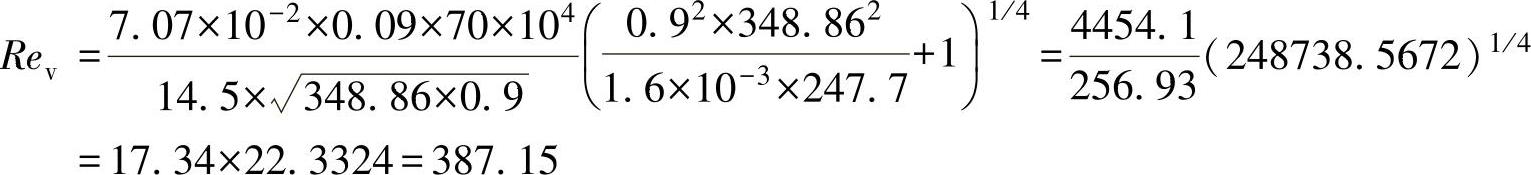
对Class900、DN300,有

Rev<10000,用Ci=1.3C,重新计算Rev。
对Class600、、DN250,有

对Class900、DN300,有

②判断C/d2>0.016N18。
对Class600、DN250,d=247.7mm。
对Class900、DN300,d=282.4mm。
N18=8.65×10-1。
故,对于Class600、DN250,C/d2=348.86/247.72=0.005685899
0.016N18=0.016×8.65×10-1=0.01384
即 C/d2<0.016N18
故,对于Class900、DN300,C/d2=371.3567/282.42=0.004656524
0.016N18=0.016×8.65×10-1=0.01384
即 C/d2<0.016N18
③计算FR。
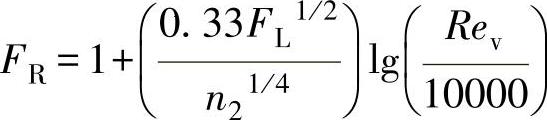
对于Class600、DN250,有

对于Class900、DN300,有
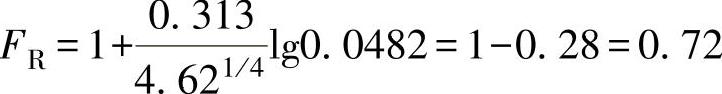
层流状态下,对于Class600、DN250,有

层流状态下,对于Class900、DN300,有

④判断C/FR与Ci的关系。
对于Class600、DN250,有
348.86/0.71=491.35>453.518
故 C/FR>Ci
对于Class900、DN300,有
371.3567/0.72=515.77>482.7637
故 C/FR>Ci
⑤选取流量系数C。
对于Class600、DN250,有
C=453.518×130%=589.5734
对于Class900、DN300,有
C=482.7637×130%=627.5928
6)确定调节阀额定流量系数。调节阀额定流量系数是调节阀出厂时调节阀所具有的流量系数。额定流量系数与阀类型、口径等因素有关。口径越大,额定流量系数越大。通常,调节阀流路越复杂,额定流量系数越小。例如,同口径低噪声调节阀的额定流量系数要比直通单座调节阀小,同口径蝶阀比直通单座阀的额定流量系数大等。
根据调节阀的计算流量系数(用C表示)、所选调节阀的固有流量特性等,确定调节阀的额定流量系数(用C100表示)。在确定额定流量系数后需要核算调节阀开度、实际可调比等数据。检查它们是否满足工艺过程控制和操作的要求。如果不满足,则需要重新选调节阀额定流量系数,并进行核算,直到满足所需要求。
计算流量系数的圆整。对调节阀计算流量系数进行圆整的原因如下:
①调节阀制造商提供的额定流量系数与计算流量系数不可能一致,因此要对计算流量系数进行放大,并圆整到调节阀制造商能够提供的额定流量系数。
②调节阀计算流量系数是最大流量工况下的计算值,没有考虑一定的操作裕度,因此要进行必要的放大。
③通常,希望调节阀在最大流量时的开度为80%。对不同流量特性的调节阀,在最大流量时的开度不同。例如,固有可调比为30的调节阀,线性流量特性调节阀的开度为79.3%,等百分比流量特性调节阀的开度为93.4%。因此,选用线性流量特性调节阀时,通常要放大一级,而选用等百分比流量特性调节阀时,需放大二级。
④不同压降比S下,最大流量时调节阀开度也有变化,因此需考虑压降比的影响。
计算流量系数C圆整的经验方法是:向上圆整一级或圆整二级。圆整后的流量系数是调节阀额定流量系数C100。也可按相对开度确定应放大的倍率k,C100=kC。
所需的放大倍率与相对开度的关系见表3-50。
对于Class600、DN250的计算流量系数C=589.5734。
阀门开度为85%,所需倍率为1.666。
额定流量系数C100=kC=1.666×589.5734=982.23
对于Class900、DN300的计算流量系数C=627.5928。
阀门开度为85%,所需倍率为1.666。
表3-50 所需放大倍率与相对开度的关系(R=30)

额定流量系数C100=kC=1.666×627.5928=1045.57。
7)计算调节阀开度。不同流量特性调节阀,其开度计算公式不同。压降比S为1时开度计算如下:
对于Class600、DN250,有

当R=30时,
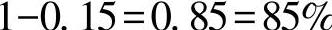
对于Class900、DN300,有
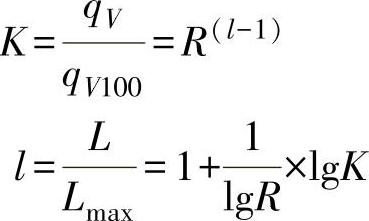
当R=30时,
8)调节阀套筒开孔面积的计算及套筒开孔尺寸和排列的建议。
①等百分比调节阀的流量特性。等百分比流量特性也称为对数流量特性,它是指单位相对位移变化所引起的相对流量变化与此点的相对流量成正比关系。即调节阀的放大系数是变化的,它随相对流量的增大而增大。其数字表达式为

于是

已知边界条件:l=0时,qV=qVmin;l=L时,qV=qVmax。
于是有
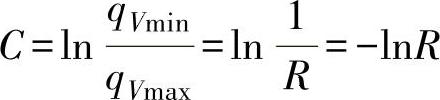
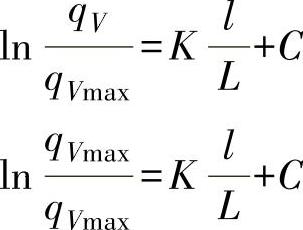
ln1=K+C
0=K+(-lnR)
即 K=lnR
代入后得

得 
或 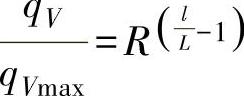
此式表明,等百分比流量特性调节阀的相对行程与相对流量的对数成比例关系,即在半对数坐标上,流量特性曲线呈现直线。在直角坐标上流量特性曲线是一条对数曲线。由于 ,即相对流量的对数与相对行程成正比,因此等百分比流量特性也称为对数流量特性。也就是说,套筒相对开孔面积的对数与相对行程成正比。
,即相对流量的对数与相对行程成正比,因此等百分比流量特性也称为对数流量特性。也就是说,套筒相对开孔面积的对数与相对行程成正比。
不同行程位置的相对流量变化量见表3-51。
表3-51 等百分比流量特性调节阀相对行程和相对流量的关系(R=30)

为了和直线流量特性进行比较,同样以行程的10%、50%、80%三点进行研究。行程变化量为10%、计算R=30时等百分比流量特性调节阀。当行程变化量为10%时,不同行程位置的相对流量变化量相对行程变化10%,在相对行程10%处,相对流量的变化为

相对行程变化10%,在相对行程50%处,相对流量的变化为

相对行程变化10%,在相对行程80%处,相对流量的变化为

说明等百分比流量特性的调节阀在不同开度下,相同的行程变化引起相对流量的变化是相等的,因此称为等百分比流量特性。等百分比流量特性调节阀在全行程范围内具有相同的控制精度。等百分电流量特性调节阀在小开度时,放大系数较小,因此调节平稳。在大开度时,放大系数较大,能有效进行调节,使调节及时。理想的等百分比流量特性曲线在线性流量特性曲线的下部,表示同样的相对行程下,等百分比流量特性调节阀流过的相对流量要比线性流量特性的调节阀少。反之,在同样的相对流量下,等百分比流量调节阀的开度要大些。因此,为满足相同的流通能力,通常选用等百分比流量特性调节阀的公称尺寸DN要比线性流量特性控制的公称尺寸DN要大些。
②确定调节阀的公称尺寸DN。根据额定流量系数KV值,查有关调节阀的生产厂家的样本,确定公称尺寸DN。
对Class600,qVmax=70×104m3/h。额定流量系数KV=982.23。
选用DN250调节阀,其内径按ASMEB16.34—2009非强制附录A选择,内径d=247.7mm。
对Class900,qVmax=90×104m3/h。额定流量系数KV=1045.57。
选用DN300调节阀,其内径按ASMEB16.34—2009非强制附录A选择,内径d=282.4mm。
③额定行程L的确定。根据调节阀的流量特性要求为等百分比流量特性。如额定行程L选择太小,如1/4d,则呈快开流量特性,无法控制。额定行程L选择过大,则势必增大调节阀的结构,使执行机构和驱动装置较为难选,同时也增加调节阀的成本。根据调节阀的结构要求,调节阀的额定行程宜选择(40%~60%)DN。
结合本国产化产品,对于Class600、DN250,额定行程选择为L=120mm;对于Class900、DN300,额定行程选择为L=120mm。
④套筒开孔截面积的计算:
根据 和相对行程,以及相对行程和相对流量的关系,计算每一相对行程位置对应的通道横截面积。
和相对行程,以及相对行程和相对流量的关系,计算每一相对行程位置对应的通道横截面积。
对于Class600、DN250,阀门额定通道横截面积:
 ;开度0位=1603.86mm2;开度10%位=651.66mm2;开度20%位=913.67mm2;开度30%位=1285.98mm2;开度40%位=1801.33mm2;开度50%位=2538.24mm2;开度60%位=3539.31mm2;开度70%位=5009.05mm2;开度80%位=7031.92mm2;开度90%位=9883.23mm2;开度100%位=13885.65mm2。
;开度0位=1603.86mm2;开度10%位=651.66mm2;开度20%位=913.67mm2;开度30%位=1285.98mm2;开度40%位=1801.33mm2;开度50%位=2538.24mm2;开度60%位=3539.31mm2;开度70%位=5009.05mm2;开度80%位=7031.92mm2;开度90%位=9883.23mm2;开度100%位=13885.65mm2。
对于Class900、DN300,阀门额定通道横截面积:
 ;开度0位=2084.7mm2;开度10%位=959.71mm2;开度20%位=1187.59mm2;开度30%位=1671.52mm2;开度40%位=2341.37mm2;开度50%位=3299.21mm2;开度60%位=4626.4mm2;开度70%位=6510.77mm2;开度80%位=9140.12mm2;开度90%位=12846.25mm2;开度100%位=18048.61mm2。
;开度0位=2084.7mm2;开度10%位=959.71mm2;开度20%位=1187.59mm2;开度30%位=1671.52mm2;开度40%位=2341.37mm2;开度50%位=3299.21mm2;开度60%位=4626.4mm2;开度70%位=6510.77mm2;开度80%位=9140.12mm2;开度90%位=12846.25mm2;开度100%位=18048.61mm2。
⑤套筒开孔尺寸和排列的建议:
对于Class600、DN250,如图3-132所示。
对于Class900、DN300,如图3-133所示。
(3)扇形阀瓣 在扇形阀瓣内,介质所通过的开启截面是阀座与阀瓣表面之间,在断面AA的垂直面上的投影所形成的圆扇形孔(图3-134)。
开启截面积

或 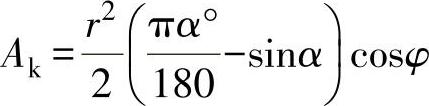
在阀瓣上制做一个或几个切口的扇形阀瓣,仅适用于通过能力很小的小规格的调节阀。
本节所探讨的是压力损失在2.5MPa以下的、适用于液体介质中的一般工业用调节阀的计算。
在计算其他工作条件与上述的条件区别很大的调节阀时,必须将上面计算中的附加因素考虑在内。

图3-132 ClaSS6OO、DN25O额定行程12Omm开孔图

图3-133 ClaSS9OO、DN3OO额定行程12Omm开孔图
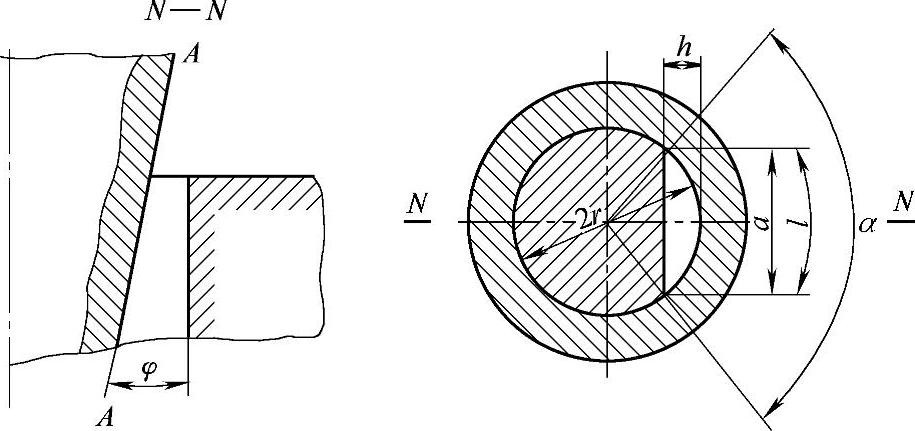
图3-134 扇形阀瓣形面的绘制
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




