为保证调节阀具有固定的流量特性曲线,对于连续调节的调节阀,需要采用复杂的异形阀瓣。流量特性曲线取决于阀门的公称通过能力qy(或流量系数KV),以及阀瓣开启高度h。
阀瓣的流量特性曲线有以下几种:直线、抛物线及等比(对数)特性曲线。通常用直线特性曲线,其次是对数特性曲线,而抛物线则很少采用。
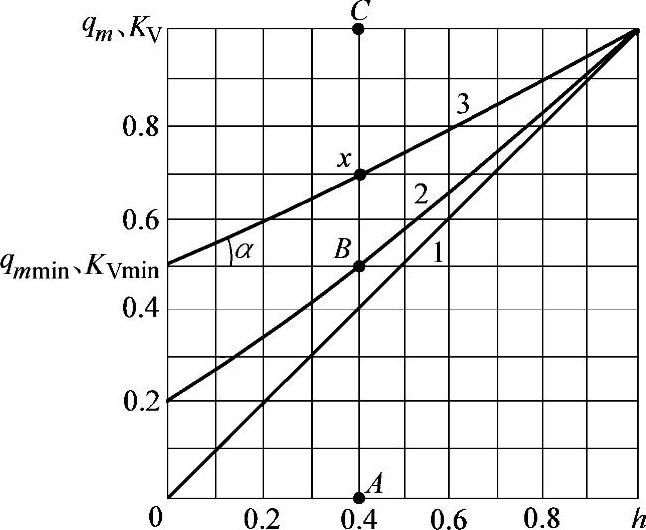
图3-112 直线特性曲线
1—qmmin=0 2—qmmin=0.2 3—qmmin=0.5
1.直线特性曲线
直线特性曲线能保证介质的质量流量qm与阀瓣的位移h(除阀瓣降至可调节行程范围内的极点位置外)成正比关系。一般这种关系可写成不通过坐标原点的直线方程(图3-112):
qm=Ch+qmmin (3-100)
式中,C为常数,它与阀的结构和尺寸,以及介质和压力降都有关, ;qmmin为介质的最小流量(h=0时)。
;qmmin为介质的最小流量(h=0时)。
调节阀通常做成当阀瓣关闭时,在qmmin=0的情况下,其阀瓣的行程与流量的关系,可表示成通过坐标原点为qm=Ch的直线。
调节阀阀瓣的行程与流量的关系以绝对值表示。如以相对值表示,其方程式应改为

式中,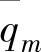 为介质质量流量,在调节范围内,用与最大流量qmmax的比值(%)表示,即
为介质质量流量,在调节范围内,用与最大流量qmmax的比值(%)表示,即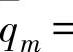
 x;
x; 为介质的最小(不可调节的)质量流量,用比值
为介质的最小(不可调节的)质量流量,用比值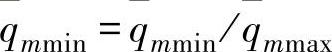 表示;
表示; 为对应于流量
为对应于流量 的阀瓣位移,以比值
的阀瓣位移,以比值 表示(hn为总调节行程或可调节的行程);
表示(hn为总调节行程或可调节的行程); 为常数,其值为
为常数,其值为 ,当
,当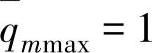 和
和 时,
时, 将此C值代入式(3-101),可得相对位的直线特性曲线方程式:
将此C值代入式(3-101),可得相对位的直线特性曲线方程式:

当 时,方程式变为
时,方程式变为

阀瓣的直线特性曲线方程式还可用图解法(图3-112)求得。如x点的流量qm为

但 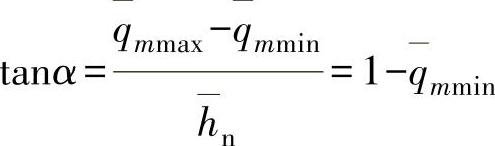
式(3-102)反映了介质流量与阀瓣开启高度所对应的直线变化关系,即方程式本身就表示阀瓣的工作特性曲线。
介质的质量流量与介质的密度和流速有关,与调节阀的结构要素无关。为了绘制阀瓣的内特性曲线,必须撇开这些因素。
当给定调节阀的工作参数条件(介质、压力损失、温度)时,阀的质量流量即与公称通过能力qmy(或流量系数KV)成正比,因此阀瓣的特性曲线方程式则为
qmy=Cyh+qmymin (3-104)
且当qmymax=0时,有
qmy=Cyh
式中,qmy为当阀瓣处于所研究位置时,阀门的公称通过能力;Cy为常数。采用相对值 以及相应的
以及相应的 ,可得到前面类似的方程式为
,可得到前面类似的方程式为
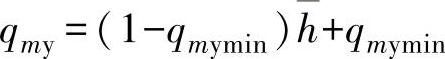
此式为阀瓣的直线内特性曲线。当阀的压力损失恒定,并且系统的阻力(不包括阀门在内)不大时,能保证获得直线特性曲线。相对值qm、 和
和 ,可从0~1变化。
,可从0~1变化。
2.抛物线流量特性曲线
抛物线流量特性曲线如图3-113所示,它能保证以下关系:
qm=Ch2+qmmin (3-105)
当qmmin=0时,有 qm=Ch2
阀门的流量与阀瓣的开启高度以相对值表示。
正如直线流量特性曲线方程式(3-105)那样,可得

和

当 ,
, 时,则
时,则 ,由此
,由此 ,公式改成
,公式改成

当 时
时

此式表示阀瓣的抛物线特性曲线。
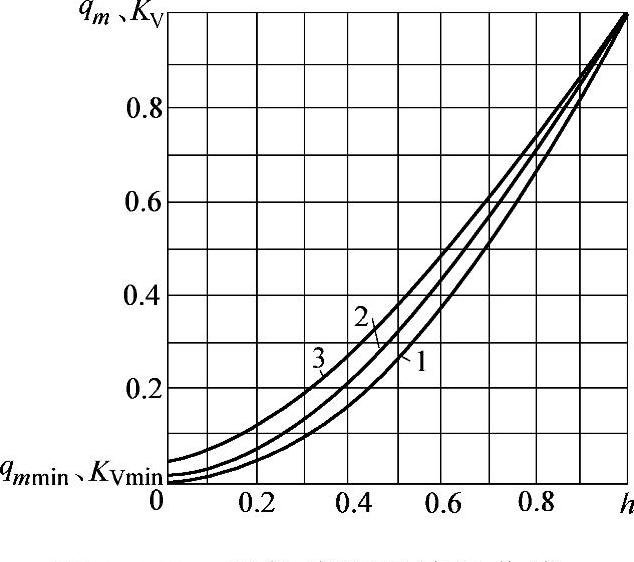
图3-113 抛物线流量特性曲线
1—qmymin=0 2—qmymin=0.02 3—qmymin=0.04
公称通过能力qmy以相对值的关系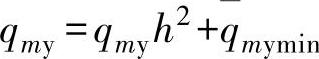 表示,则有
表示,则有

这一方程式为阀瓣的抛物线内特性曲线。当阀门压力损失恒定,且系统阻力(不包括阀门在内)不大时,能保证阀瓣的工作特性曲线为抛物线。
3.对数流量特性曲线
对数流量特性曲线如图3-114所示,它能保证 的关系。在对数特性曲线情况下,首先是阀瓣的行程与介质流量成正比。因此,阀瓣升高,其流量按比例增加,于是特性曲线便由此而得名。将
的关系。在对数特性曲线情况下,首先是阀瓣的行程与介质流量成正比。因此,阀瓣升高,其流量按比例增加,于是特性曲线便由此而得名。将 移项,并将等式两边积分,得
移项,并将等式两边积分,得

以相对值表示

式中, 为当
为当 时的介质流量;C为常数。
时的介质流量;C为常数。
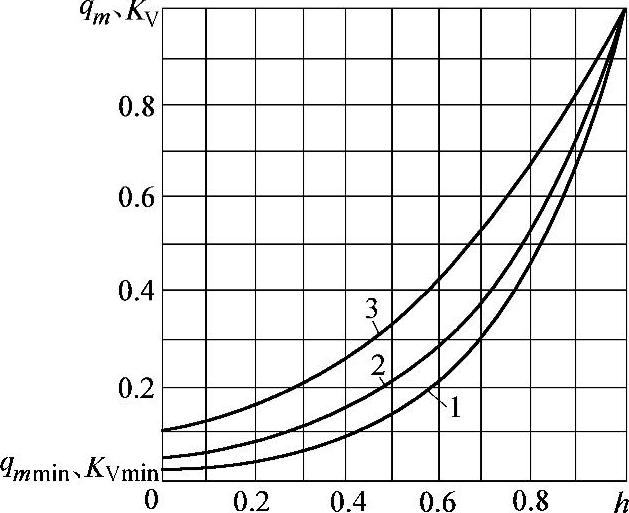
图3-114 对数(等比)流量特性曲线
1—qmymin=0.02 2—qmymin=0.04 3—qmymin=0.1
常数值可用下述方法求得

当

及
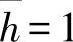
时,得

,由此得

。因此有
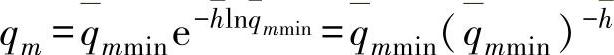
最后得
这就是等比(对数)特性曲线(图3-114)方程式。
为了绘制阀瓣的对数内特性曲线,将方程式中的公称通过能力用相对值表示,则有

按有关标准,最小调节流量系数KV和KVmin,对于双座式调节阀等于0.04,单座式调节阀等于0.02。
对数特性曲线调节阀的公称通过能力,当最小相对调节流量 时,列于表3-44;当
时,列于表3-44;当 时,列于表3-45。(https://www.xing528.com)
时,列于表3-45。(https://www.xing528.com)
表3-44 当qmymin=0.02时,对数特性曲线调节阀的qmy值

表3-45 当qmymin=0.04时,对数特性曲线调节阀的qmy值

如果以符号KV(流量系数)表示,则内特性曲线方程式将变为以下形式:
1)在为直线特性曲线时,有
KV=Cyh+KVmin (3-107)
当KVmin=0时,有KV=Cyh
以相对值表示:

当 时;有
时;有

2)在为抛物线特性曲线时,有
KV=Cyh2+KVmin (3-108)
当KVmin=0时,有 KV=Cyh2
以相对值表示:

当 时
时
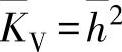
3)在为对数特性曲线时,有

利用所给定的特性曲线相对应的任一演变公式,便可确定阀瓣在各种位置的介质流量。根据此流量,可求出阀瓣在阀座中的开启截面尺寸,以及该阀瓣的尺寸和形状。
上面所推导的公式,可以确定当调节阀的压力损失恒定情况下的内特性曲线。实际上,阀门的压力损失只是系统压力损失的一部分,而且阀门的压力损失是随调节阀的开启程度而变的。这种情况会引起外特性曲线失真,即所得到的工作特性曲线与内特性曲线两样。
现在来研究不可压缩液体中阀门的工作情况,假定管道中的阻力为常数,系统(不包括阀门)的阻力系数为ζT=常数,而阀门的压力损失ΔpK则随介质的流量而变。根据假定条件,得
ΔpK=ΔpC-ΔpT
式中,ΔpC为整个系统(包括阀门)的压力损失;ΔpT为不包括阀门的系统压力损失。
ΔpT值与管路中介质流速的平方成正比,因而也与流经管路的介质流量的平方成正比,故

式中,ΔpTσ为当介质为最大流量时,系统(不包括阀门)的压力损失。
将ΔpT代入ΔpK值中,得
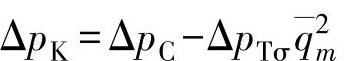
令 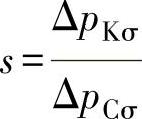
式中,ΔpKσ为在调节范围内,当介质为最大流量时调节阀的压力损失;ΔpCσ为在调节范围内,当介质为最大流量时,整个系统(包括阀门)的压力损失。
前面已推导出:

两式相除,得

将ΔpK值代入,得

由此,得
故 
于是,有 
但 ΔpTσ=ΔpCσ-ΔpKσ
故 
将式中的ΔpC/ΔpCσ提出,约去 ,并以
,并以

代之,得

令ΔpC/ΔpCσ=n,可得

在整个系统(图3-115)中,应压力损失ΔpC=ΔpCσ恒定,以及n=1时,得

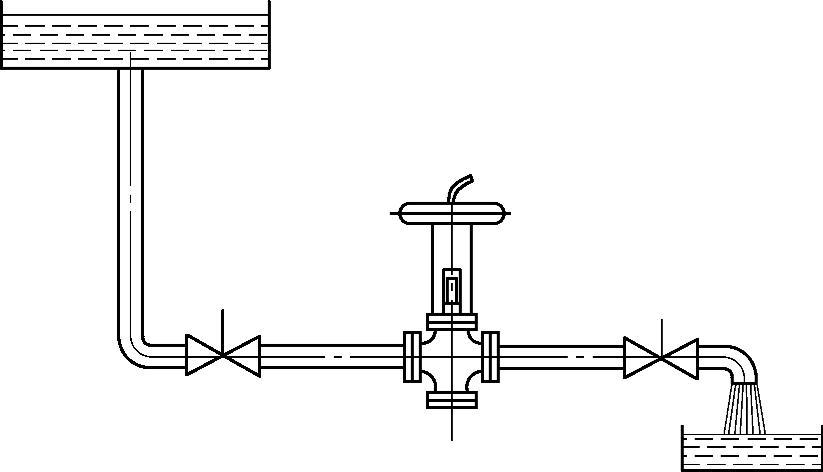
图3-115 系统中压头恒定时的阀门工作示意图
在给定s值时,对于处在不同位置的阀瓣,代入不同的 值,即得出所给定条件的工作特性曲线。
值,即得出所给定条件的工作特性曲线。
在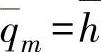 (当
(当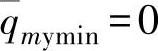 时)的直线的特性曲线时,如果系统压力损失恒定,则可绘出如图3-116所示各种s值的特性曲线。对于
时)的直线的特性曲线时,如果系统压力损失恒定,则可绘出如图3-116所示各种s值的特性曲线。对于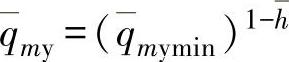 的对数内特性曲线,当
的对数内特性曲线,当 时,各种s值的特性曲线如图3-117所示。采用类似的方法,还可绘出各种
时,各种s值的特性曲线如图3-117所示。采用类似的方法,还可绘出各种 值的特性曲线。
值的特性曲线。
假如阀门是在带有泵的系统中工作,则系统中压力损失经常发生变化。这种情况使得计算更为复杂,因为要考虑泵的特性曲线,所以还必须确定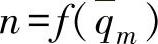 的关系。
的关系。
图3-116和图3-117所示的内特性曲线表示,假如在阀门中产生的压头与系统总压头相比,阀门占的比例不大,则阀门的工作特性曲线与内特性曲线相比差别很大。
当调节阀处于全开位置时,鉴于阀门的压头占系统总压头的绝大部分(0.8或更高),在阀瓣为直线特性曲线时,则可近似地认为阀瓣的位移使流量成比例变化。如果当调节阀处于全开位置时,阀门的压头低于0.8倍系统总压头,仅阀瓣为直线特性曲线,也不能保持正比关系。
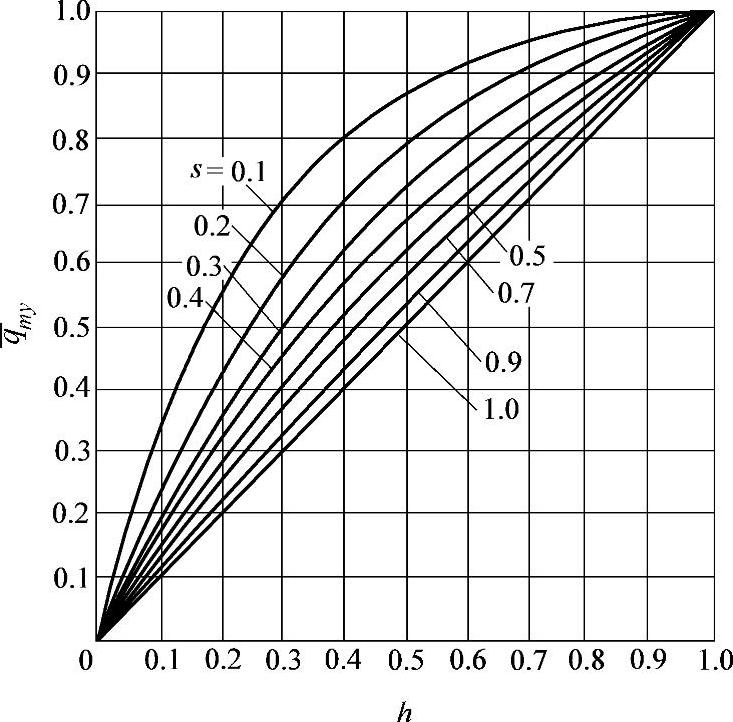
图3-116 在直线内特性曲线时,各种 s值的特性曲线(系统中压力损失为常数)

图3-117 在对数内特性曲线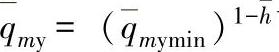 下时,各种s值的特性曲线(系统中压力损失为常数)
下时,各种s值的特性曲线(系统中压力损失为常数)
从对图3-117所示的对数内特性曲线图分析得知,当s值很小时,具有对数内特性曲线的阀门能保证其工作特性曲线接近于直线;同时,具有直线内特性曲线的阀门,当s值很小时,绘成的工作特性曲线远离直线。
在绝大多数情况下,必须保证调节阀为直线工作特性曲线。在选择阀瓣时,必须考虑s值。当s值大时,为保证阀在直线特性曲线下工作,可采用直线内特性曲线阀瓣;当s值小时(0.4或更小),采用对数内特性曲线阀瓣比较合理。当qmymin=0.02~0.04时,采用对数内特性曲线,可得到阀在接近直线的工作外特性曲线下工作。当采用一般阀门厂生产的备用阀瓣时,这种方法是可行的。
在设计调节阀阀瓣时,当给定s值,以及系统压力损失的变化情况下,阀瓣的内特性曲线可以调整,以确保得到所需的外特性曲线,如直线、对数曲线等。
由前面推导出的公式,可得

式中, 。
。
对于系统压力损失恒定的情况,当n=1时

在给定s值时,代入不同的 值,就得到
值,就得到 值。在为直线外特性曲线时,
值。在为直线外特性曲线时,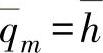 (如果
(如果 ;在为对数特性曲线时,
;在为对数特性曲线时,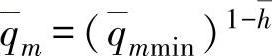 。因此,给定了外特性曲线,就可确定所需要的内特性曲线。
。因此,给定了外特性曲线,就可确定所需要的内特性曲线。
这样,在不同的s值(图3-116)时,为了获得所需要的直线特性曲线,可以近似地取相对于s=1的直线(通过坐标原点与水平成45°的直线)。该直线为平滑的反映工作情况的特性曲线,如图3-116所示。
对于可压缩介质(气体和蒸汽)是否可采用调整特性曲线的方法尚未最后证实。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




