1.立柱横梁式支架
(1)截止阀、调节阀支架 立柱横梁的螺纹部分截面如图3-103b所示。其截面积Ac按式(3-68)确定:

式中,Ac为立柱顶端螺纹心部的截面积(mm2);FT为阀杆总轴向力(N);[σ]为材料的许用应力(MPa)。
阀门在关闭过程中,两立柱的顶端螺纹受拉,而在开启过程中,支柱横梁下面的平直部分受压。这部分直径大小可以不予计算,因为支柱中部的圆的直径,比顶部螺纹部分要大得多,其强度足够。
横梁由两支柱支撑,在中心最大轴向力FT的作用下,它受弯曲应力和切应力。
确切地说,载荷并不通过“横梁”的几何中心,而是作用在驱动螺杆的外径d3的圆周上,如图3-103a所示。如果横梁上的螺母是锒套的,甚至还要偏远些,如图3-103b所示。
横梁的有效宽度按式(3-69)计算:

式中,bo为横梁的有效宽度(mm);L为螺栓孔轴线之间的距离(mm)(图3-103a);h为横梁的厚度(mm),由所需的螺纹旋合长度确定。
螺纹旋合长度HT(图3-103),按式(3-70)计算:

式中,HT为螺纹旋合长度(mm);ts为螺纹的螺距(mm);[pb]为螺纹螺旋旋合表面上的许用比压(MPa),推荐[pb]=7MPa;d3为螺纹大径(mm);d4为螺纹根部直径(mm)。
无论螺纹是直接在横梁上,还是在镶套上,HT都是螺纹旋合长度。假如是在镶套上,则横梁厚度h小于HT。考虑反复使用后的磨损,HT的最小值不能小于d3+6mm。
(2)闸阀支架 图3-109所示为闸阀常用的立柱横梁式支架。
1)立柱上部根径按式(3-71)计算:
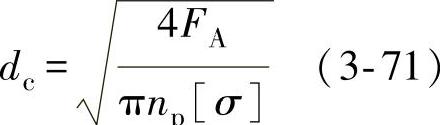
式中,dc为立柱上部根径(mm);FA为阀杆总轴向力(N);np为立柱数量,一般为2根,在高压大口径阀门中,有时采用4根立柱;[σ]为应用应力(MPa)。
2)横梁中心处的有效深度按式(3-72)计算:
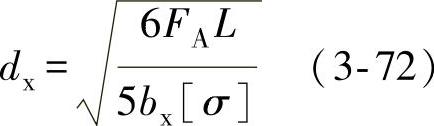
式中,dx为横梁中心处的有效深度(mm);L为螺栓孔轴线之间的距离(mm);bx为横梁中心处的有效宽度(mm)。
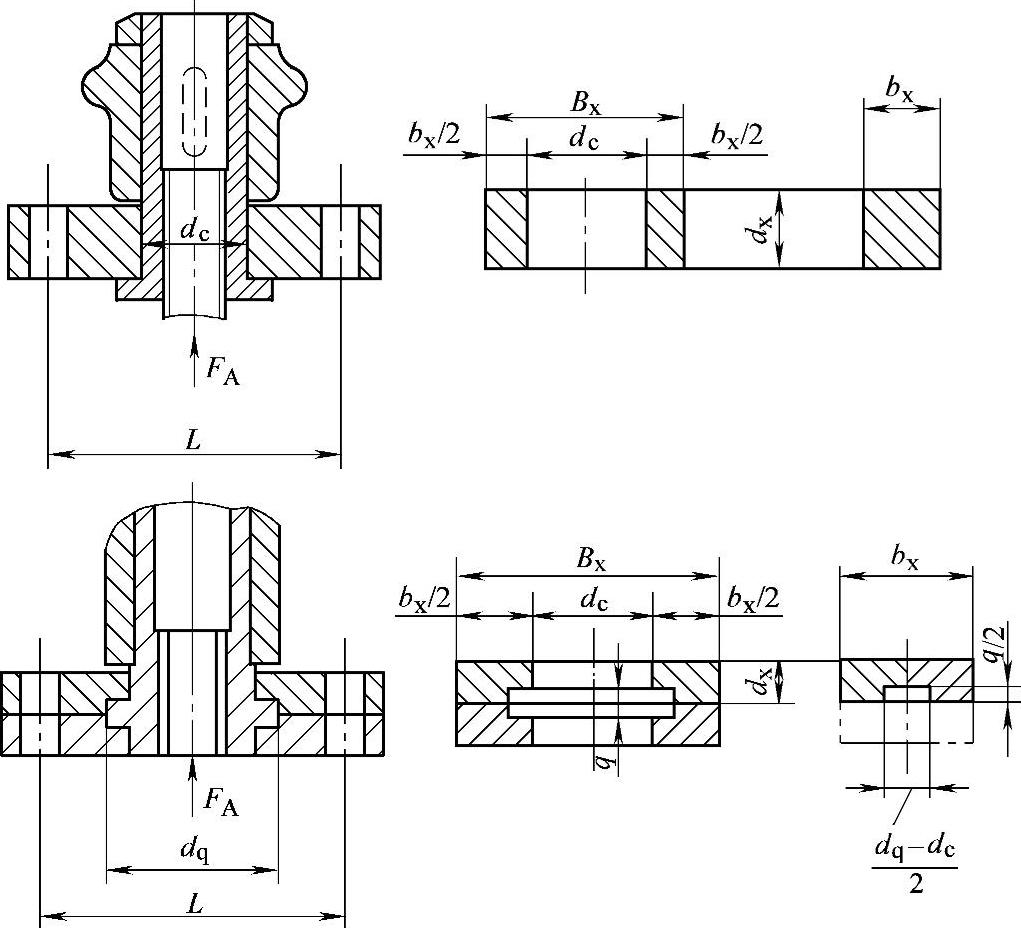
图3-109 闸阀的立柱横梁式支架
2.整体支架的计算
整体支架包括阀杆螺母式支架及法兰连接式支架。其受力情况比较复杂,可将其作为超静定的固定桁架,在其中间部分受到阀杆轴向力Fz′的作用来计算。
(1)闸阀支架 其闸阀支架的典型结构如图3-110所示。必须分别检验Ⅰ—Ⅰ、Ⅱ—Ⅱ、Ⅲ—Ⅲ截面处的应力。
1)Ⅰ—Ⅰ截面处的合成应力按式(3-73)校核:
σ∑Ⅰ=σWⅠ+σLⅠ+σNWⅠ≤[σL] (3-73)
式中,σ∑Ⅰ为Ⅰ—Ⅰ截面的合成应力(MPa);σWⅠ为弯曲应力(MPa);σLⅠ为拉应力(MPa);σNWⅠ为力矩引起的弯曲应力(MPa);[σL]为材料的许用拉应力(MPa)。
①σWⅠ按式(3-74)计算:

式中,MⅠ为弯曲力矩(N·mm);WyⅠ为Ⅰ—Ⅰ断面对y轴的截面系数(mm3),按表3-43计算。
MⅠ按式(3-75)计算:
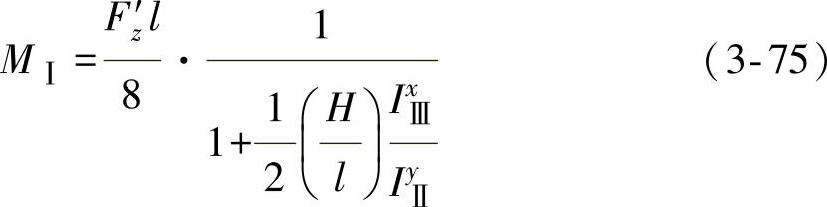
式中,l为框架两重心之间的距离(mm);IxⅢ、IyⅢ分别为Ⅲ—Ⅲ截面对x轴和Ⅱ—Ⅱ截面对y轴的惯性矩(mm4),按表3-43计算;H为框架高度(mm);
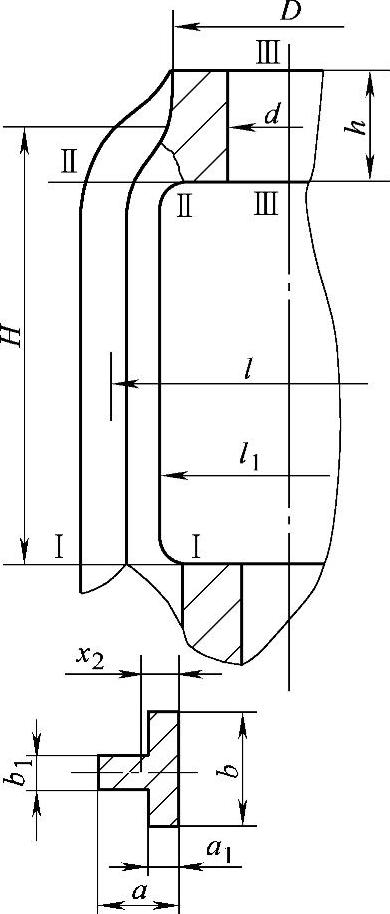
图3-110 闸阀支架
l按式(3-76)计算:
l=l1+2x2 (3-76)
式中,x2为框架形心位置,根据截面形状按表3-43计算。
②σLⅠ按式(3-77)计算:

式中,AⅠ为Ⅰ—Ⅰ截面的面积(mm2),按表3-43计算。
③σNWⅠ按式(3-78)计算:

式中,MNⅢ为力矩(N·mm);WxⅠ为Ⅰ—Ⅰ截面对x轴的截面系数(mm3),按表3-43计算。
MNⅢ按式(3-79)计算:

式中,MFJ为阀杆螺母和支架间的摩擦力矩(N·mm)。
2)Ⅱ—Ⅱ截面的合成应力按式(3-80)校核:
σ∑Ⅱ=σWⅡ+σLⅡ≤[σL](3-80)
计算方法与Ⅰ—Ⅰ截面相同。
3)Ⅲ—Ⅲ截面的弯曲应力按式(3-81)校核:
 (https://www.xing528.com)
(https://www.xing528.com)
式中,MⅢ为Ⅲ—Ⅲ截面的弯曲力矩(N·mm);WxⅢ为Ⅲ—Ⅲ截面对x轴的截面系数(mm3),按表3-43计算。
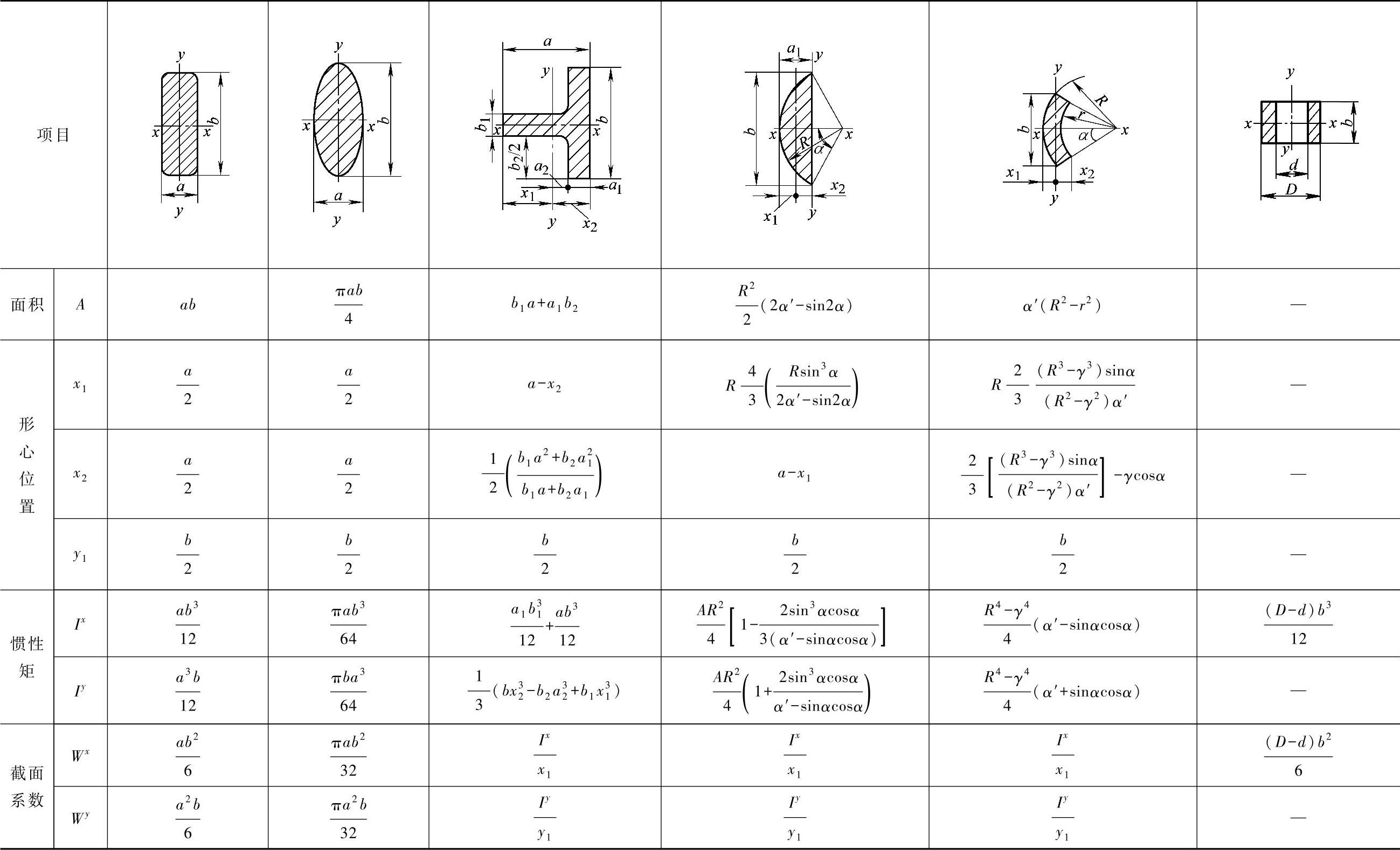
表3-43 截面的特性
注: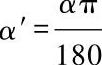 ,表示弧度。
,表示弧度。
MⅢ按式(3-82)计算:

(2)截止阀、节流阀支架 其典型结构如图3-111所示。必须分别检验Ⅰ—Ⅰ、Ⅱ—Ⅱ、Ⅲ—Ⅲ、Ⅳ—Ⅳ截面处的应力。
1)Ⅰ—Ⅰ截面的合成应力 按式(3-83)校核:
σ∑Ⅰ=σWⅠ+σLⅠ+σNWⅠ≤[σL] (3-83)
式中,σWⅠ为弯曲应力(MPa);σLⅠ为拉应力(MPa);σNWⅠ为力矩引起的弯曲应力(MPa)。
①σWⅠ按式(3-84)计算:

式中,MⅠ为弯曲力矩(N·mm)。
MⅠ按式(3-85)计算:
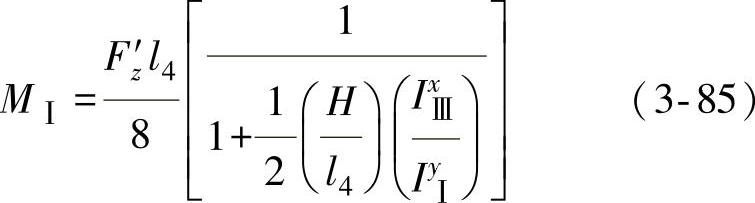
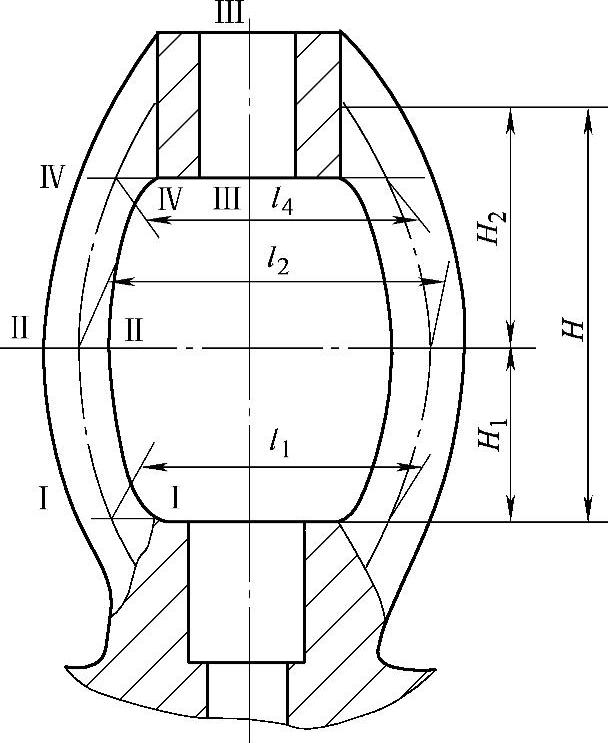
图3-111 截止阀、节流阀支架
②σLⅠ按式(3-86)计算:

③σNWⅠ按式(3-87)计算:

式中,MNⅠ为力矩(N·mm)。
MNⅠ按式(3-88)计算:

2)Ⅱ—Ⅱ截面的合成应力按式(3-89)校核:
σ∑Ⅱ=σWⅡ+σLⅡ+σNWⅡ≤[σL] (3-89)
式中,σWⅡ为弯曲应力(MPa);σLⅡ为拉应力(MPa);σNWⅡ为力矩引起的弯曲应力(MPa)。
①σWⅡ按式(3-90)计算:

式中,MⅡ为Ⅱ—Ⅱ截面弯曲力矩,MⅡ=MⅠ。
②σLⅡ按式(3-91)计算:

③σNWⅡ按式(3-92)计算:

式中,MNⅡ为力矩(N·mm)。
MNⅡ按式(3-93)计算:

3)Ⅲ—Ⅲ截面的弯曲应力按式(3-94)校核:

式中,MⅢ为Ⅲ—Ⅲ截面的弯曲力矩(N·mm)。
MⅢ按式(3-95)计算:

4)Ⅳ—Ⅳ截面的合成应力按式(3-96)校核:
σ∑Ⅳ=σWⅣ+σLⅣ≤[σL] (3-96)
式中,σWⅣ为Ⅳ—Ⅳ截面弯曲应力(MPa);σLⅣ为Ⅳ—Ⅳ截面拉应力(MPa)。
①σLⅣ按式(3-97)计算:

②σWⅣ按式(3-98)计算:

式中,MⅣ为Ⅳ—Ⅳ截面弯曲力矩(N·mm)。
MⅣ按式(3-99)计算:
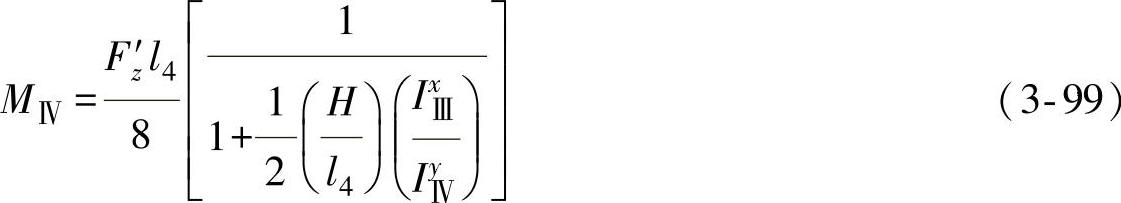
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




