液面调节对象特性分析

设在图2-13中，罐的流出量q_Ve与液体的液面高度z无关。按照这个假设，给出液面高度z和流量q_V1、q_Ve之间的动态微分方程式为

式中，A为罐的横截面积。

调节对象的动态特性是用液面最大变化速度来表征的。这个变化速度是当流入量q_V1取最大值q_V1100，而流出量q_Ve是零时出现的。在这种情况下，液面最大变化速度为

类似的另一种最大流量出现的情况，是在q_V1=0，而q_Ve有最大值q_Ve100时。

图2-13 液面调节对象

例如，如果q_V1100=60m³/h，A=1.5m²，液面变化的最大速度为

按液面变化的速度值，可作如下分类：

1）低变化速度。W_max<1mm/s。

2）中变化速度。W_max≈10mm/s。

3）大变化速度。W_max>100mm/s。

当消除干扰产生的偏差时，液面的迅速变化可出现相当大的过调。从结构的观点出发，在上述的假设条件下，图2-13所示的罐是个一阶对象。

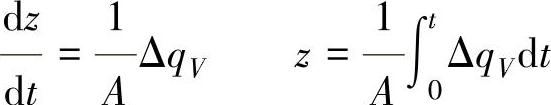(www.xing528.com)

在图2-14所示为阶跃信号和产生的响应特性曲线。

仅当罐的出口只有一个泵，或者在液面上有较大压力时，流出量q_Ve与液面z无关的假设才能成立。在第一种情况下，当液面有比较小的变化时，泵的流量是个常数。这是实际上可以实现的。

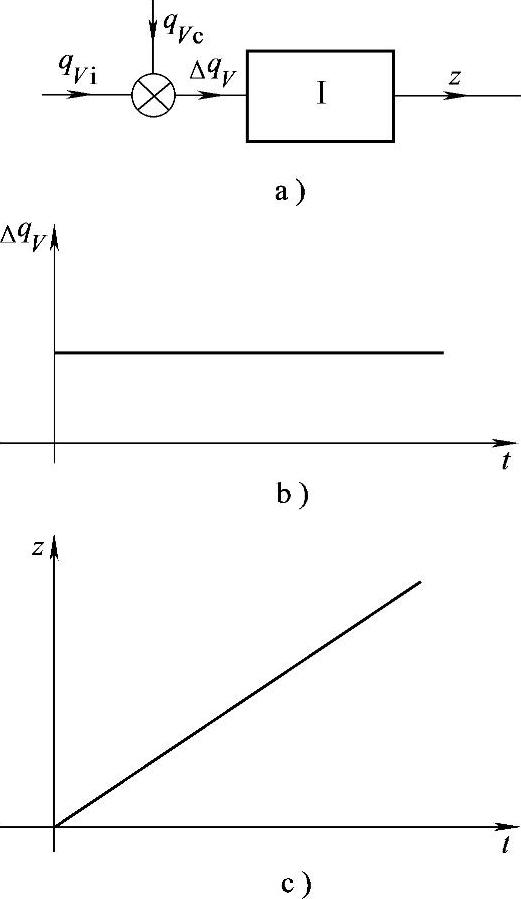
图2-14 液面调节

a）原理图 b）输入的阶跃信号 c）响应特性曲线

【例2-2】 一个分馏塔塔底液面高度z=1.5m，这个塔和后面工艺设备之间的压差是0.4MPa，液体的密度ρ=700kg/m³。已知后一设备的流量取决于两容器间的压差p₁-p₂=0.4MPa。试问液面对流量有何影响。

解 两个罐间液体的流量计算式为

式中，K_V为流量系数（对塔底出口调节阀而言）；g为重力加速度。

忽略液面的影响，式（2-18）可变为

式（2-19）与式（2-18）相比，得

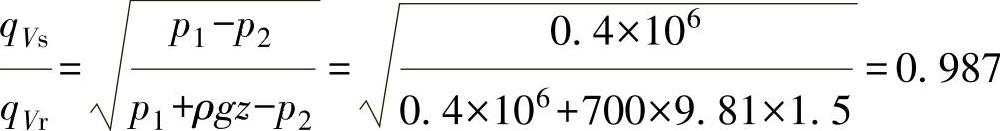
这证明，用简化式（2-19）计算流量q_Vs，与用考虑液面影响的复杂式（2-18）计算的流量q_Vr相比，仅差1.5%，故实际上关系不大。但是，在目前的示例中，塔底能够看作是一个积分元件，动态特性曲线的描述用式（2-17）。当液体从一个常压罐流到另一个常压罐时，其流量仅取决于两罐的液位差。在这种情况下，罐不是一个积分元件，而是一个非周期元件，流量与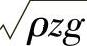成比例。该项数值小，所以对于这样的情况，要选用具有大的K_Vs的调节阀。这也是在大多数的情况下，在罐出口设置泵以输送液体的原因之一。