选择调节阀的最佳特性曲线优化指南

这里所用调节阀的“最佳工作特性曲线”一词，是指在具体的工作条件下，保证阀门在流量变化的整个范围内，有一个不变的放大系数。在这种情况下，设想系统的其他元件也是线性的，对于信号变化的整个范围，能够实现调节器的最佳工作。实际上，这些要求只有在极个别的情况中才能遇到。在大多数的情况下，除了放大系数取特定范围内的数值，上述要求是不能实现的。

当流量自动调节系统的给定为常数时，调节阀放大系数的变化问题不大。因为在有固定工作点的情况下，总能够实现最佳调节。在改变系统的给定，从而改变给定工作点的情况下，为使流量自动调节系统重新达到最佳状态，必须重新调整调节器的参数。在改变流量自动调节系统给定（如串级调节、跟踪调节等）的情况下，不能达到系统的最佳状态。因为工作点在整个范围内变化时，放大系数的变化有可能引起系统振荡。

根据上述情况，在规定工作条件时，要选择最合适的调节阀特性曲线，就要选用能保证放大系数变化最小的曲线形式。在这方面主要考虑下面几个因素：

1）固定或是变化给定值q_V1的调节。

2）有没有开方器。

3）参数ψ=Δp_r100/Δp_s。

4）管路阻力的变化，将引起参数ψ的变化。

5）介质密度。

在这些因素中，液体密度变化对调节阀特性的影响是次要的。但对可压缩介质，尤其在特殊的流动状态下，密度变化对调节阀特性的影响是重要的。

图1-63介绍了对于不同的参数ψ值，线性和对数调节阀的放大系数变化。为了分析流量自动调节系统，在没有开方器的情况下，应确定调节阀-管路-孔板-变送器系统放大系数的变化。为此目的，要考虑函数x=F（H）的导数。式中：x是变送器的输出值，H是调节阀的开度。

所要求的结果，可以由式（1-52）的导数dq/dh和式（2-8）的导数dx/dq的乘积求得。这个结果表示在图2-9和图2-10中。图2-9所示为h的函数，图2-10所示为q的函数。

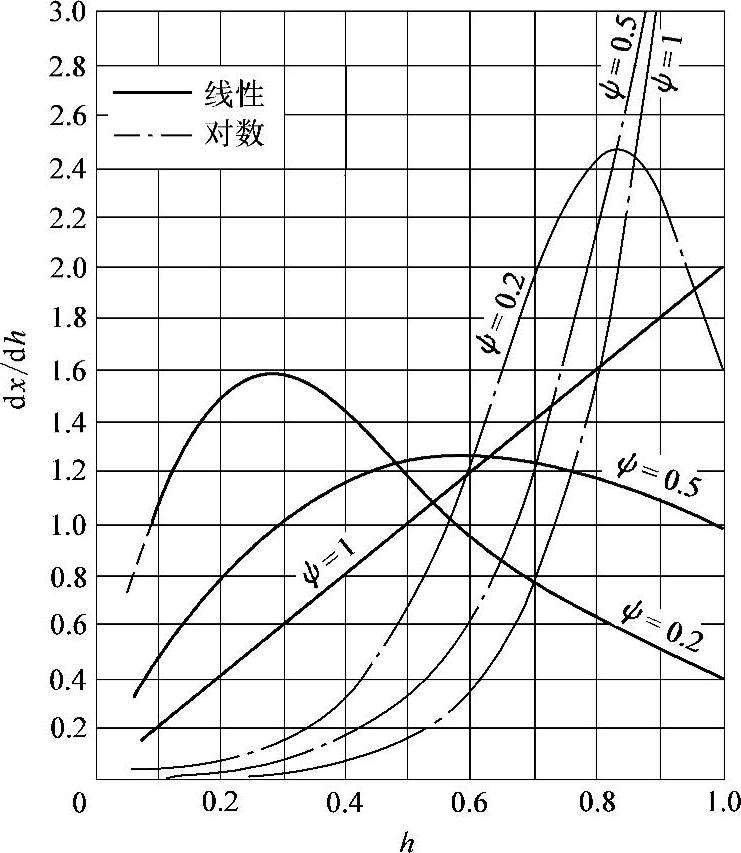
图2-9 在没有开方器时，调节阀-管路-孔板-变送器系统放大系数随开度h的变化

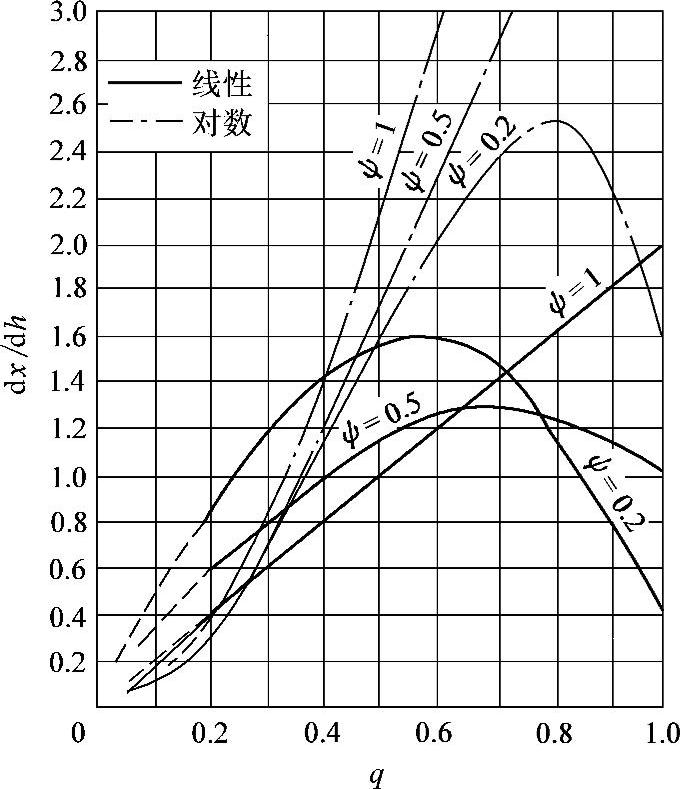
图2-10 在没有开方器时，调节阀-管路孔板-变送器系统放大系数随流量q的变化

从图2-9和图2-10可以看到，对于调节阀-管路-孔板-变送器系统，在没有开方器的流量自动调节系统中，当ψ=0.2～1时，线性调节阀与对数调节阀比较，变化是比较小的。

【例2-1】 在一个没有开方器的流量自动调节系统中，对数调节阀开度为60%（h=0.6），安装调节阀的管路系统参数ψ=0.2。试确定调节阀-管路-孔板-变送器系统的放大系数。

图2-11 【例2-1】的功能图

解 在标准座标中，变送器的放大系数等于1。同样，管路的放大系数K=1。在这个基础上，静态时这四个串联元件的等效系统如图2-11所示。

由图1-64b得

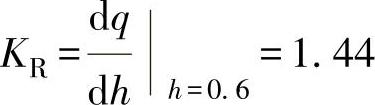
对于h=0.6和ψ=0.2，由图1-62表示的调节阀工作特性曲线，求得流量值q=0.43。此时孔板的放大系数[参考式（2-8）]为

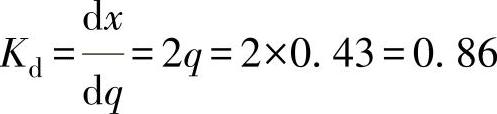
这样，元件系统的传送系数为

K=K_RK_d=1.44×0.86=1.283

由图2-9能够直接确定出a点，如在h=0.6的情况下，K=1.24。

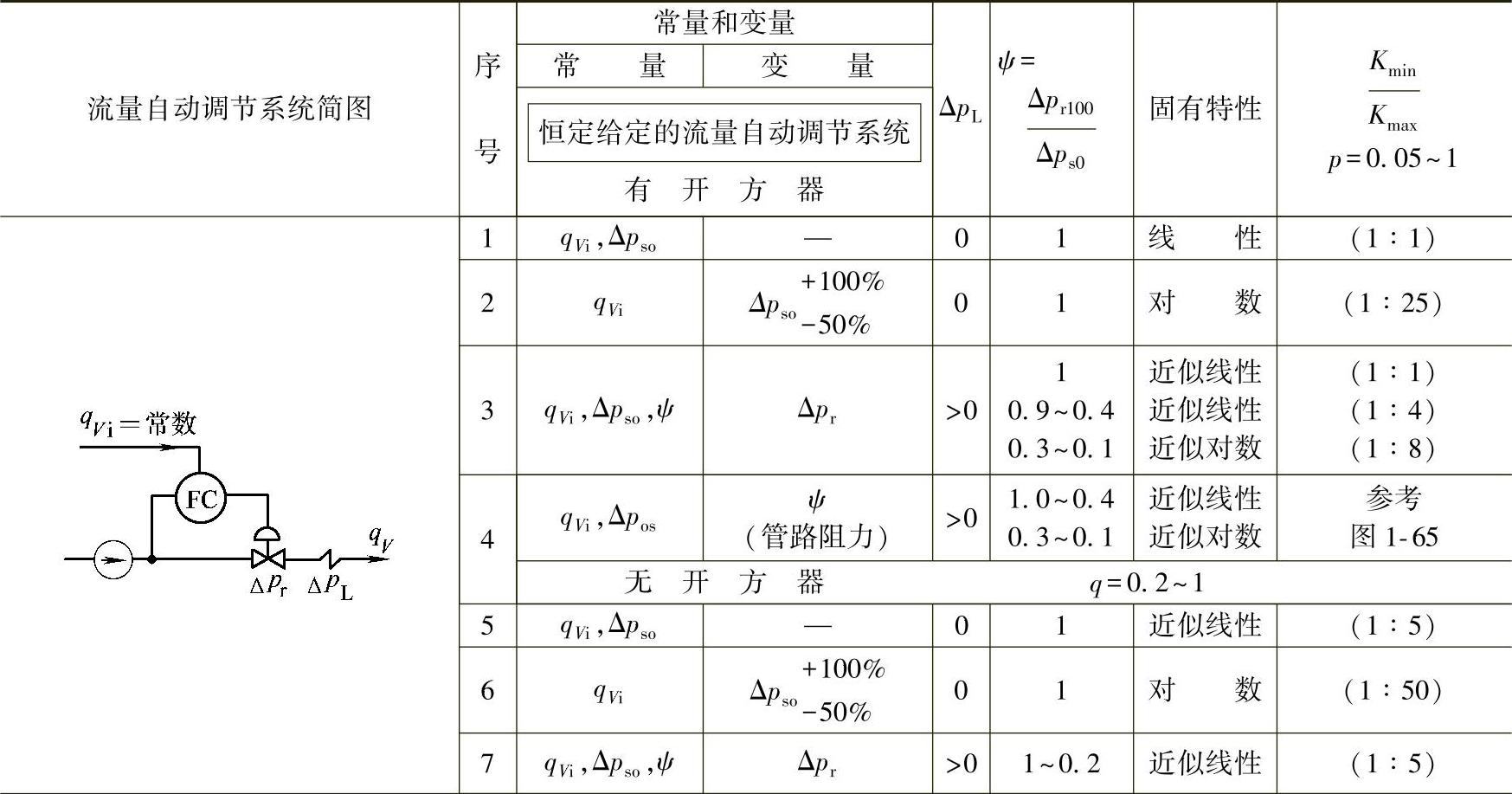
在表2-1中，介绍了实践中有重要意义的参数配合。由于流体密度的影响小，故没有包含在表中。对于每种组合，指出了放大系数变化为最小的固有特性。

每种情况求解的方法是比较复杂的，超出了本书的范围。这些情况求解的基础是调节阀和变送器的固有特性和放大系数（有或无开方器）。现举例说明对表中序号6情况求解的方法。

因Δp_L=0，ψ=1，式（1-109）变为

在第6种情况下，管路系统上的压力损失全部加在调节阀上（Δp_r=Δp_s），它是可变的。流量的给定值q_V是个常数。通过调节阀的介质流量是在给定值附近有微小的变化。

将式（2-12）对h求导数，得

表2-1 流量自动调节系统调节阀最佳特性的选择

（续）(www.xing528.com)

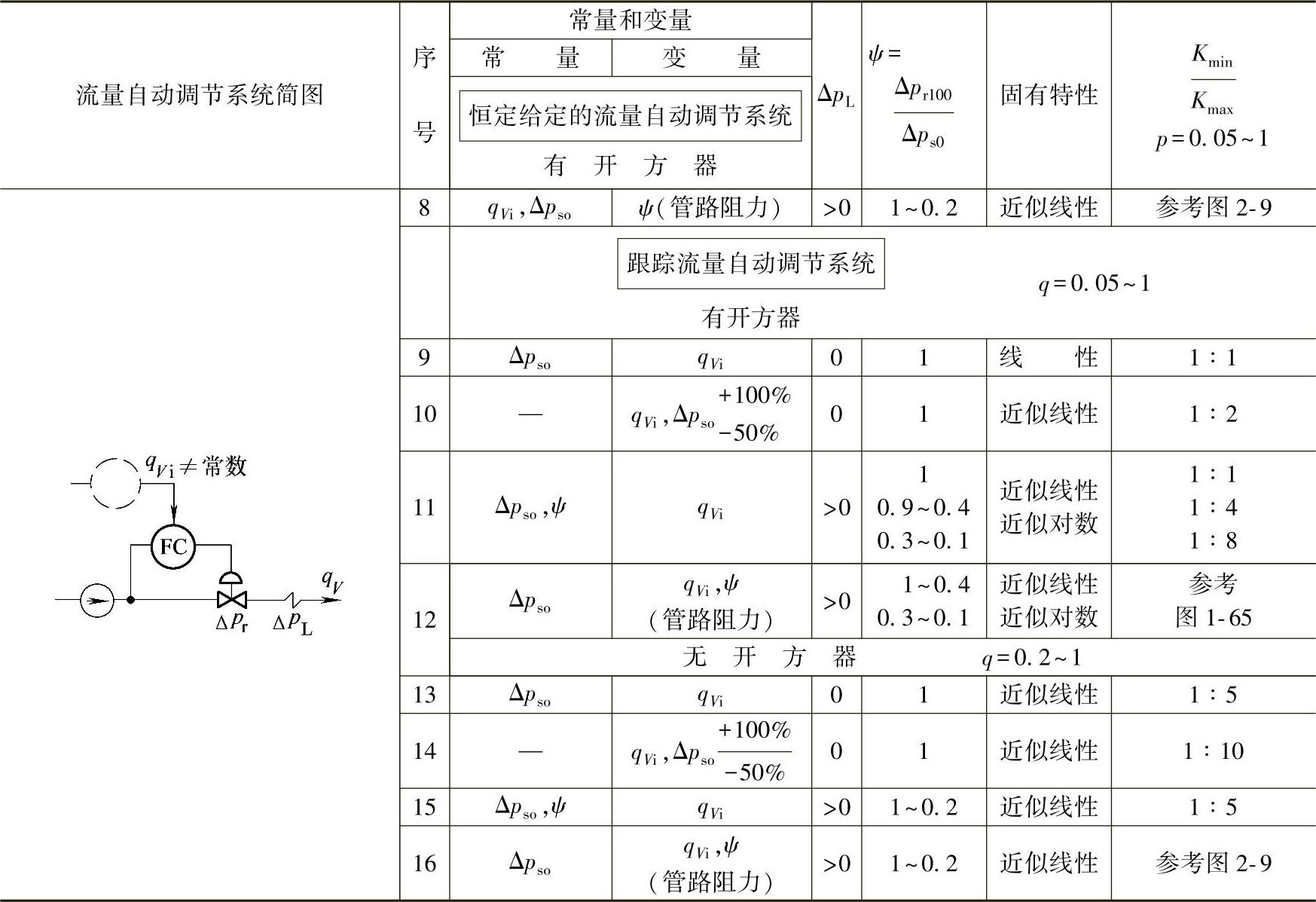
对于具有式（1-41）所示的对数静态特性的调节阀，式（2-13）变为

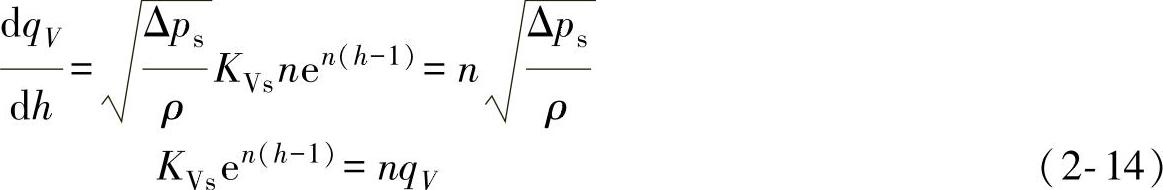
因此，调节阀的传递系数为

K_R=dq_V/dh=nq_V （2-15）

由于q_V=q_V1=常数，因此当调节阀上的压力损失Δp_r变化时，流量没有变化。

图2-12所示为对应调节阀不同压力损失Δp_s的线性和对数调节阀的静态特性，可调比是1∶50。从图中还可以看到，对于q_V=常数的对数调节阀，工作特性的斜率一定；而对于线调节阀，斜率是变化的。

当q_V=常数时，带孔板的变送器传递系数K_d[式（2-8）]同样是常数。

因为q_V=常数时，K_R和K_d是常数，所以对于第6种情况，使用对数特性调节阀是正确的解答。

如果流量自动调节器的给定q_V，在q=0.2～1的整个范围内变化，则

在图2-12b中，对于曲线Δp_so+100%，有

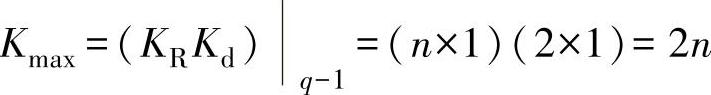
在图2-12b中，对于曲线0.5Δp，有

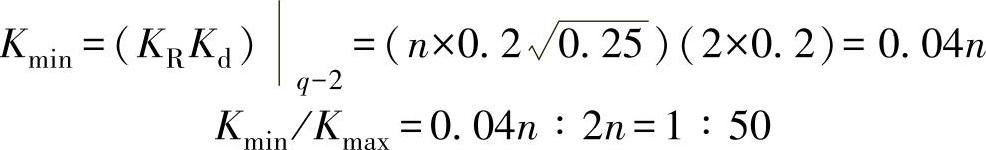
因而在表2-1中，序号6的最后一栏是（1∶50）。

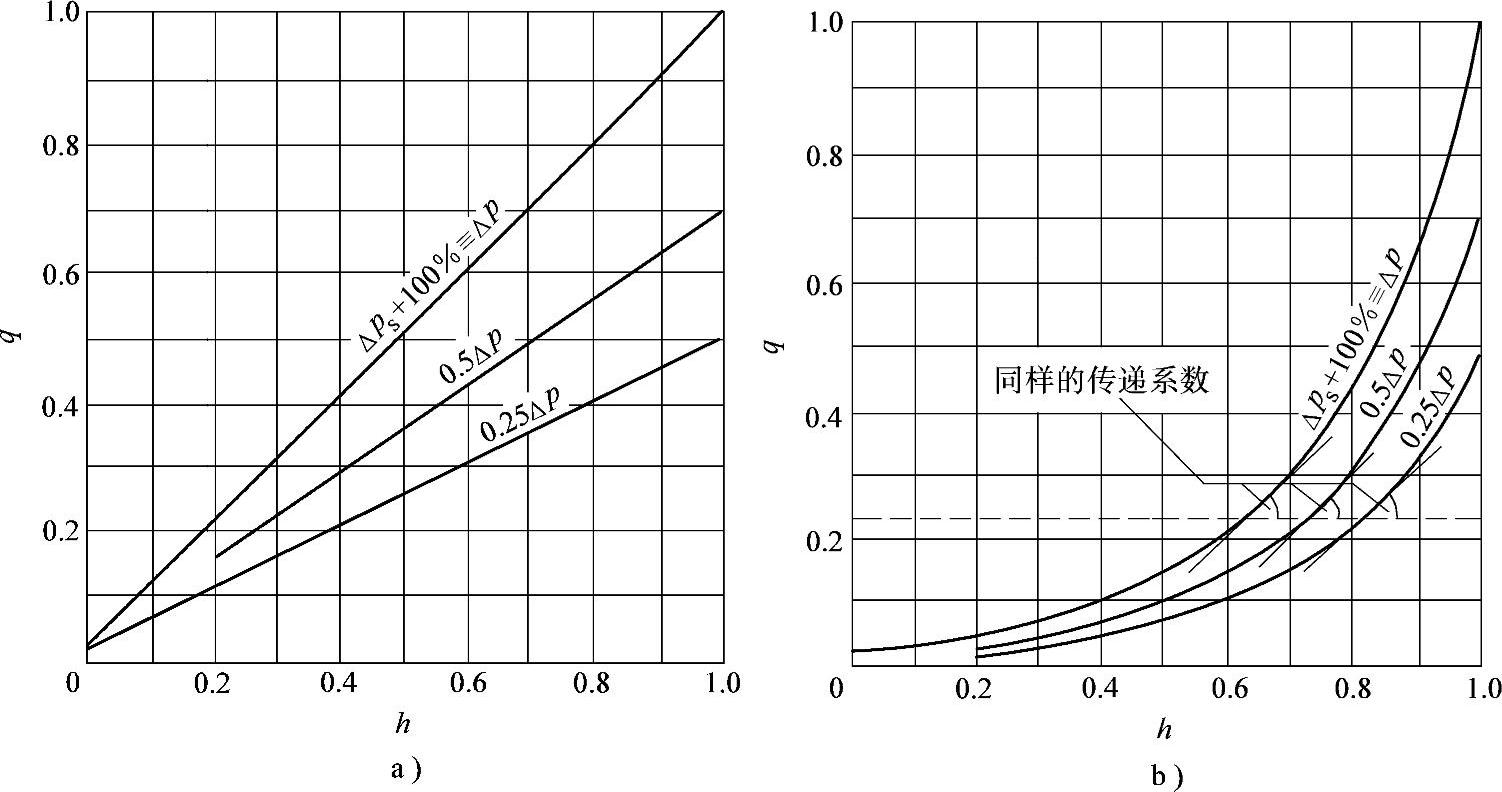
图2-12 调节阀的静态特性曲线（可调比为1∶50）

a）线性特性曲线 b）对数特性曲线

注：条件为Δp_L=0（ψ=1）；Δp_r=Δq^+100%_s-50%。

表2-1包含了12种重要情况的综合结果，它们可以分为两类：定值流量自动调节系统；跟踪流量自动调节系统。

每类又可分为两组：有开方器的和没有开方器的。

在第3和第4栏中，注明了关系到选择阀门特性的常量和变量。第5栏表明管路是否存在压力损失Δp_L。第6栏表明参数ψ的数值范围或数值。第7栏中介绍按常量、变量和前面栏中的参数ψ值，应选择的特性形式有：

1）线性。此时线性静态特性代表正确的解。

2）近似线性。此时线性静态特性代表近似的解。

3）近似对数。此时对数静态特性代表近似的解。

近似解（如近似对数）和K_min/K_max值（如1∶61），表示给定q_V1变化时，相应的解是近似的，以及相应的放大系数变化范围。相反，如果q_V1=常数，解是准确的，K_min/K_max值是1∶1。

在表的最后一栏中，给出了比率K_min/K_max。它表示放大系数的变化所对应的流量范围。对于有开方器的变送器，流量变化范围q=0.05～1；对于无开方器的变送器，q=0.2～1。在后一种情况下，q<0.2不被使用，因为如变送器的输出q=0.2，则x=q²=0.04，这对应于整个范围的4%。

由表2-1可看出，大多数情况下，放大系数有较大的变化。对于恒定给定的流量自动调节系统，仅当给定是在非常大的范围内变化时，比率K_min/K_max才有重要意义。

跟踪流量自动调节系统用于q=0.05～1范围，个别的是q=0.2～1。放大系数大幅度变化时，必然要修正调节器的参数值。

对于表2-1，需要对参数ψ加以说明。参数ψ在第3行栏内是个常数，但是在第6栏内则是在1～0.1之间。另一方面，参数ψ在第4栏内是个变量，在第6栏内也是在1～0.1之间，看上去是相同的。

对于第3种情况，参数ψ对于每个具体情况是常数值。例如，如果ψ=0.4，也就是在具体的应用范围内保持这个数位。

其他都属于第4种情况。

在具体的应用中，参数ψ不是常数，而经常在1～0.1范围内变化。在这种情况下，管路阻力是变化的，例如改变调节阀的开度，在换热器的排放位置等。Δp_L100的变化与Δp_r100之间的关系为

Δp_so=Δp_r100+Δp_L100

Δp_L100的变化，引起Δp_r100的变化（假设Δp_so是个常数），也就是参数ψ的变化。