阀门执行机构的动态特性分析

调节阀的输入是阀杆的行程，而输出则是阀门流出液体的流量。这个液体流量是指紧靠调节阀的阀后流量。这一流量根据导管的动态特性，传送到自动化控制系统。

作为自动化系统的元件，调节阀带有执行机构，因此分析阀门-执行机构的动态特性更为方便。这一集合体的输入是控制信号（电或气），输出则是液体的流量。

图1-94所示为调节阀的计算简图。

从垂直方向力平衡得

式中，m为活动部分的质量；H为阀杆行程；μ为由黏性引起的摩擦因数；F_P为流体在阀芯上的压力差产生的力；F_s为作用力（执行机构产生的）。

如果阀门被一个气动执行机构所作用，如图1-95所示，则力F_s的表达式为

F_s=Ap_m-λH （1-128）

式中，A为膜片的计算面积；p_m为膜片上的压力；λ为弹簧刚度。

图1-94 调节阀的计算简图

a）调节阀的活动部分 b）等效力学简图

图1-95 膜片式执行机构作用下的计算简图

a）调节阀的活动部分 b）等效力学简图

将式（1-128）代入式（1-127），得

为了在式（1-129）中显示出流量-调节阀的输出，用式（1-109）来表达阀杆的行程与流量（通过K_V）之间的关系，即

式（1-129）和式（1-130）组成了调节阀动态数学模型。(www.xing528.com)

为了获得比较简单的q_V/q_V100=f（H）表达式，式（1-105）可在工作点H=H₀附近进行线性化，即

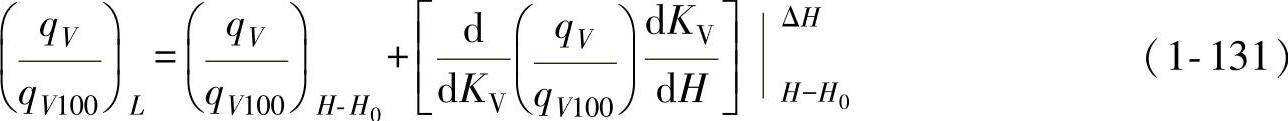
当选择调节阀在接近线性静态特性的情况下，线性化关系式可以近似地表达实际的静态特性，此时式（1-131）可使用在阀门行程的整个区间。

如果对于介质压差作用于阀芯产生的力F_P取某一中间值，式（1-129）可变为

式中，ΔH=H-H₀；Δp_m=p_m-p_mo。

式（1-127）可写为

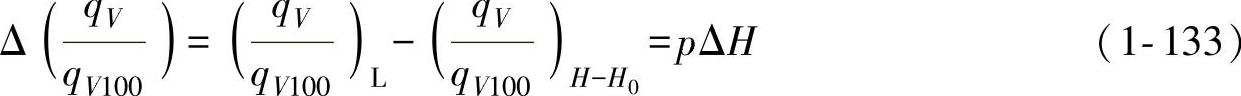
其中

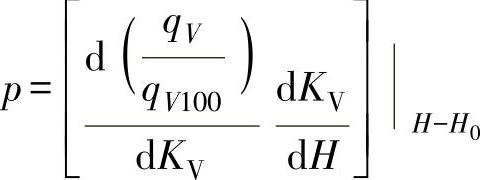
将式（1-133）代入式（1-132），得

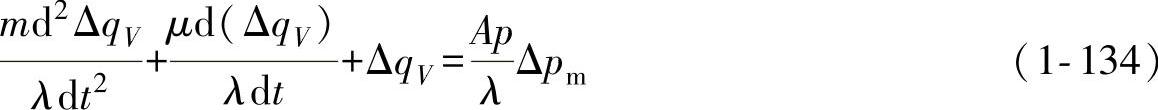
其中，q_V=q_V/q_V100。

对微分方程式（1-134）进行拉普拉斯变换，并写成Δq_V（s）/ΔP_m（s）的表达式，得

式中，a₂=m/λ；a₁=μ/λ；b=Ap/λ。

式（1-135）很好地描述了在工作点附近调节阀的动态特性。问题是难于对时间常数a₁、a₂和传递常数b进行数值表达。解答这些问题涉及实际工作条件下对不同尺寸和类型的调节阀进行试验研究，这需要大量的时间和材料。作为参考值，可取时间常数a₁的数值为1～2s，a₂的数值小于0.2s²。这些参考值对于调节阀来说是有效的。

[1]指下屈服强度，后同。

[2]在美国流量系数C_V定义为：当流过的水流量通过调节阀产生的压力损失是1lb/in²时，单位是gal（美）/min（U.S.gallon/min）。C_V和K_V之间的换算关系为：C_V=1.156K_V，或K_V=0.858C_V。