滚动轴承尺寸公差与旋转精度规定详解

答：滚动轴承公称尺寸有公称内径、公称外径和公称宽度（图156）。

公称内径d是指包容公称圆柱孔理论内孔表面的圆柱体的直径，或在一指定的径向平面内，包容公称圆锥孔理论内孔表面的圆锥体的直径。它一般作为实际内孔表面偏差的基准值（公称直径）。

公称外径D是指包容外表面的圆柱体直径。它一般作为实际外圆表面偏差的基准值（公称直径）。

套圈公称宽度B（内圈）或C（外圈）是指套圈两理论端面间的距离。它一般作为实际宽度偏差的基准值（公称尺寸）。

根据滚动轴承使用性能要求及其结构特点，标准中规定了以下尺寸公差与旋转精度要求。

下述公差用术语及下标符号含义如下。

单一平面——能够进行测量的任一径向或轴向平面。

单一尺寸——任意两相对点之间测得的任意距离（局部实际尺寸）。

实际尺寸——通过测量获得的某一零件的尺寸。

S——适用于成套轴承或轴承游隙。

e——适用于外圈。

i——适用于内圈。

m——测量值的算术平均值。

p——测量所在平面。

r——适用于径向游隙。

s——单一或实测值。

w——适用于滚动体。

1、2…——直径或宽度不止一个时的标注符号，适用于套圈或组件。

（1）内径偏差

1）单一内径偏差Δ_ds——单一内径与公称内径之差，即Δ_ds=ds^-d。单一内径d_s是指与实际内孔表面和一径向平面交线相切的两条平行切线之间的距离。

2）内径变动量V_ds——单个套圈最大与最小单一内径之差，即V_ds=d_smax^-dsmin。

3）平均内径偏差Δ_dm——平均内径与公称内径之差，即Δ_dm=dm^-d。

平均内径d_m是指单个套圈最大与最小单一内径的算术平均值，即。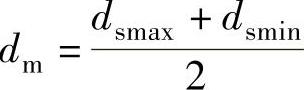

4）单一平面平均内径偏差Δ_dmp——单一平面平均内径与公称内径之差，即Δ_dmp=d_mp-d。

单一平面平均内径d_mp是指最大与最小单一平面单一内径的算术平均值，即。

5）单一平面内径变动量V_dsp——最大与最小单一平面单一内径之差，即V_dsp=d_spmax-d_spmin。(www.xing528.com)

6）平均内径变动量（公称圆柱孔）V_dmp——单个套圈最大与最小单一平面平均内径之差，即V_dmp=d_mpmax-d_mpmin。

（2）外径偏差

1）单一外径偏差Δ_Ds——单一外径与公称外径之差，即Δ_Ds=D_s-D。

2）外径变动量V_Ds——单个套圈最大与最小单一外径之差，即V_Ds=D_smax-D_smin。

3）平均外径偏差Δ_Dm——平均外径与公称外径之差，即Δ_Dm=D_m-D。

平均外径（公称圆柱外表面）D_m是指单个套圈最大与最小外径的算术平均值，即。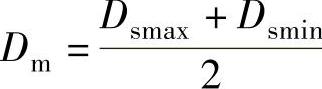

4）单一平面平均外径偏差Δ_Dmp——单一平面平均外径与公称外径之差，即Δ_Dmp=D_mp-D。

单一平面平均外径D_mp是指最大与最小单一平面单一外径的算术平均值，即。

5）单一平面外径变动量V_Dsp——最大与最小单一平面单一外径之差，即V_Dsp=D_spmax-D_spmin。

6）平均外径变动量V_Dmp——单个套圈最大与最小单一平面平均外径之差，即V_Dmp=D_mpmax-D_mpmin。

（3）宽度和高度偏差

1）套圈单一宽度偏差Δ_Bs或Δ_Cs——套圈单一宽度与公称宽度之差，即Δ_Bs=B_s-B或Δ_Cs=C_s-C。

2）套圈宽度变动量V_Bs或V_Cs——单个套圈最大与最小单一宽度之差，即V_Bs=B_smax-B_smin或V_Cs=C_smax-C_smin。

3）轴承实际宽度偏差（由内圈一端面和外圈一端面来限定轴承宽度的向心轴承）Δ_Ts——轴承实际宽度与轴承公称宽度之差，即Δ_Ts=T_s-T。

4）轴承实际高度偏差（推力轴承）Δ_Ts——轴承实际高度与公称高度之差，即Δ_Ts=T_s-T。

（4）旋转精度

1）成套轴承内圈径向圆跳动（向心轴承）K_iS——内圈内孔表面在内圈不同的角位置相对于外圈一固定点间的最大与最小径向距离之差。

2）成套轴承外圈径向圆跳动（向心轴承）K_eS——外圈外表面在不同的角位置相对于内圈一固定点间最大与最小径向距离之差。

3）成套轴承内圈异步径向圆跳动（向心轴承）K_ieS——内圈正反向旋转若干圈测量时，外圈外表面上任一固定点相对内圈内孔表面上一固定点间的最大与最小径向距离之差。

4）成套轴承内圈轴向跳动（深沟球轴承）S_iS——在距内圈轴线的径向距离等于内圈滚道接触直径一半处，内圈基准端面在内圈不同的角位置相对外圈一固定点间最大与最小轴向距离之差。

5）成套轴承外圈轴向跳动（深沟球轴承）S_eS——在距外圈轴线的径向距离等于外圈滚道接触直径一半处，外圈基准端面在外圈不同的角位置相对内圈一固定点间最大与最小轴向距离之差。

（5）内部游隙

1）径向游隙（能承受纯径向载荷的轴承，非预紧状态）G_r——在不同角方向不承受任何外载荷，一套圈相对另一套圈从一个径向偏心极限位置移到相反的极限位置的径向距离的算术平均值。

2）轴向游隙（能承受两个方向轴向载荷的轴承，非预紧状态）G_S——不承受任何外载荷，一套圈相对另一套圈从一个轴向极限位置移到相反的极限位置的轴向距离的算术平均值。