展开构件必备：相贯线的求解

在展开放样中，会有各种形体相交而成的构件，形体的表面交线称为相贯线。作相交构件的展开，必须准确地求出相贯线，依据相贯线将复杂的相交形体划分为若干基本形体的截体，再将它们分别展开。

（1）任何相交形体的相贯线，都有以下性质

1）相贯线是形体表面的共有线。

2）相贯线是形体表面的分界线。

3）相贯线是封闭曲线（形体有一定的范围）。

（2）相贯线的求法

1）素线法。相交形体的表面有积聚性投影，相贯线必积聚其中。

2）辅助平面法。用假想辅助平面截切，作两形体的截交线，交点即相贯线。

3）辅助球面法。作图的原理与辅助平面法基本相同（平面换成球面）。

（3）用素线法求三通管的相贯线（图1-42）的步骤

1）8等分（或12等分）支管的水平投影，得出各等分点。

2）按“宽相等”的原则，得侧面投影，再按“高平齐，长对正”，得出相贯线的正面投影。

（4）异径正交三通管（图1-43）相贯线的简便求法

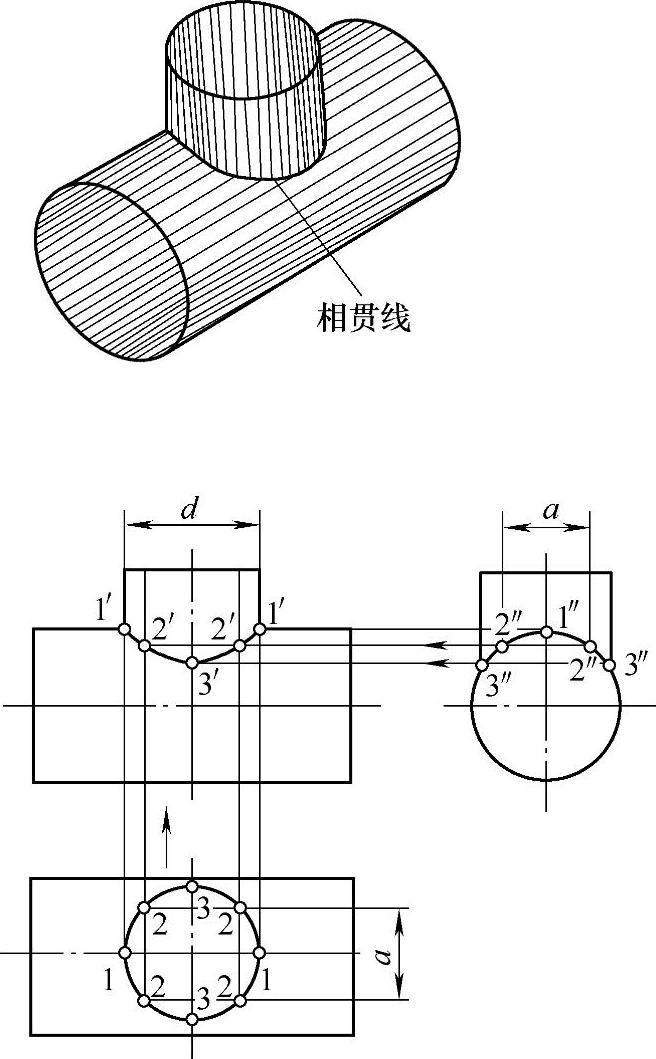
图1-42 异径正交三通管的相贯线

图1-43 相贯线的简便求法

1）主管的轴心上画出两管1/2同心断面，画出支管的1/2断面，8等分（或12等分）支管。(www.xing528.com)

2）支管的等分点沿铅垂方向投影到主管的断面圆周上，再按素线法得出相贯线的正面投影。

（5）辅助平面法求圆柱与球偏心相交的相贯线

辅助平面作法，如图1-44所示：

1）俯视图上将圆柱的圆周8等分（或12等分）。

2）按长对正得出主视图的1′、5′两点。

3）在俯视图上通过2、4两点作截平面（平行于V面）与球交于a、b两点。

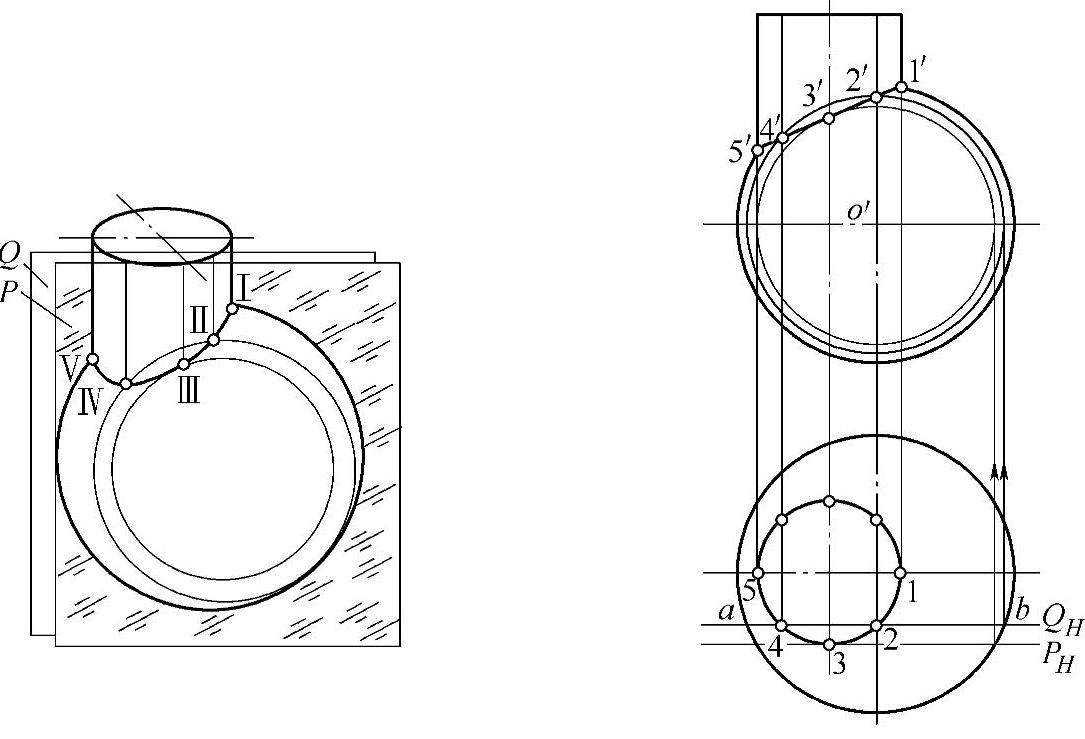
图1-44 圆柱与球偏心相交的相贯线

4）截平面截得的球体是一个圆，以O′为圆心，a2（或b2）为半径画弧，2、4两点按长对正投到主视图上，与弧的交点即为相贯线。

（6）辅助球面法求圆柱斜交圆锥的相贯线

辅助球面作法，如图1-45所示：

1）先求主视图的相贯线的最高点1、最低点4的投影。

2）以两轴的交点O为圆心，适当的弧长R为半径画弧（R的最大长度是O1，R的最小长度是O4）。

3）弧与圆柱和圆锥分别有两个交点，连接圆锥的两点和圆柱的两点，这样就会得到一个交点，这是相贯线的一个点。改变弧的半径可以得到相贯线上不同的点，连接后即为相贯线。

图1-45 圆柱与圆锥偏斜交的相贯线