定位误差统计分析与消除方法

1.统计定位误差

众所周知，侦察定位结果不仅与侦察定位系统的性能有关，同时还与定位场景有关，也即对于给定的侦察定位系统，不同的定位场景，最终的定位精度不同。同样，相同的定位场景，不同的侦察定位系统，得到的侦察定位结果也相差甚远。由于观测站、辐射源目标的运动状态时刻在变化，参数测量、目标位置解算等处理过程中的各种误差使得侦察定位结果或多或少与目标的真实位置存在一定的偏差。因此，在实际侦察定位中，定位误差必然存在，其差别仅在于度量方法及其参数大小。

2.平均误差（ME）

通常，定位误差被建模为随机过程，如果假设在某次侦察定位试验中，t=ti时刻目标的真实位置为x_i，而相应的定位结果为，则定位误差通常定义为Δ_i=，其中为了表示简化未标试验序号。为了更准确反映某定位系统在给定场景下的定位误差，通常要进行大量统计试验，并对试验结果进行统计分析，以消除时间和样本选择对侦察定位试验结果的影响。因此，统计定位误差通常表示为

该表达式即为定位误差的统计均值。

由于在实际定位应用中，目标位置的准确值是无法获取的，能够得到的只是其估计值，也即估计样本。因此，在无任何先验知识条件下，定位结果通常由样本的平均值代替，即

式中，n为样本数量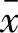；为样本均值。

因此，根据平均误差的定义，平均定位误差定义为多次定位误差的算术平均值，也是一种衡量定位精度的常用方法。其优点是定义和计算简单，但是在实际中很难操作，这是因为目标真实值永远都是未知的。一般常用的就是将多次不同定位方法所得的定位误差进行统计平均。

3.均方误差（MSE）

在数理统计中通常用均方误差描述误差，即参数估计值与真值之差平方的期望值，且有(www.xing528.com)

该统计参数描述了估计值偏离真实值的大小。

同样，由于在实际定位应用中，目标位置的准确值是无法获取的，能够得到的只是其估计值，也即估计样本。因此，定位误差的均方误差估计表达式为

式中：n为样本数量；为样本均值

根据数理统计知识，在均方误差表达式中，除以n-1为无偏估计；若除以n则为渐进无偏估计。因此，有关文献也有如下表达式：

4.均方根误差（RMSE）

均方根误差亦称标准误差，同样用来衡量观测值同真值之间的偏差，其定义为均方误差的平方根。因此在有限次定位估计中，均方根误差常用式（6-82）表示：

式中，各个参数的定义通前面均方误差。同样，也存在如下的渐进无偏估计结果：

从上面的定义可知，均方误差和均方根误差对定位误差的描述基本是一致的，两者之间为平方或开根号的关系，即。