1.基本原理
人对声源的定位主要用声音幅度这个物理量,而机器却可以精确地测量声音的相位。由于声波在空气中以一定速度传播,到达设置于不同位置的传声器的相位不同,根据这些传声器对同一声音采集时的相位差别,我们可以计算出同一声音到达每对传声器的时间差值(又叫时延值,图6-4)。
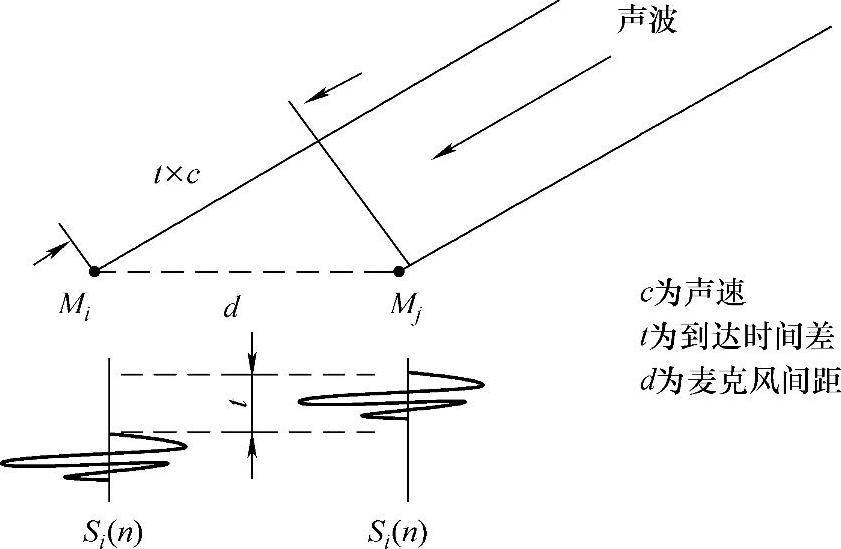
图6-4 声音时延示意图
如果我们得到了某个声源发出的声音到达一对传声器的时延值,则这个声源就处于以这对传声器所处的位置为焦点;而到达时延所对应的声音传输距离为参数的双曲面上。使用多对传声器可得到多个时延值,也就得到了多个双曲面,而声源位置就处于这些双曲面的相交点。合适的安排传声器的位置,可以使得双曲面的交点只有一个,这点就是我们要的声源位置。
在三类声源定位方法中,基于时延估计的声源定位方法复杂度最低、实现最简单,且定位精度较高,便于实现实时的系统。考虑到定位的实时性、实现的简易性和实际的需求,采用基于时延估计的声源定位方法。然而,该方法是先求取时延,再根据时延计算出声源的方位,所以在计算声源的方位时,所用的时延参数是过去时间。因此该方法求解出的声源位置在某种程度上是一个次最优的结果。此外,该方法很难适应于多声源的定位,因为多声源具有不同的空间位置;而且多声源之间的相互干扰都严重影响了时延估计的精确性。因此该方法往往应用于单声源的定位。另外,时延估计的准确性决定了声源定位的准确性,而时延估计的精度受到环境噪声和室内混响的影响。因此该方法需要一种抗噪性和抗混响性高的时延估计算法。
2.定位方法
定位的方法主要分为两大类:一种是确定目标函数用的搜索方法;一种是几何定位法。本节首先讨论麦克风和声源的几何位置;然后介绍搜索的方法;最后根据麦克风的数量和几何位置分别讨论线性修正最小均方声源定位法(含球形插值法)和线性插值声源定位法。
(1)几何定位法 假设第i对麦克分别对应矢量mi1和mi2,它们的连线为x轴,中点的矢量为mi,声源到两个麦克间的时延差为τi,则声源S应该满足矢量方程
‖rs-mi1‖-‖rs-mi2‖=τi·c (6-31)
式中,c为声速。显然满足该方程的声源S应该位于一个双曲面上。声源和麦克风的几何位置如图6-5所示。
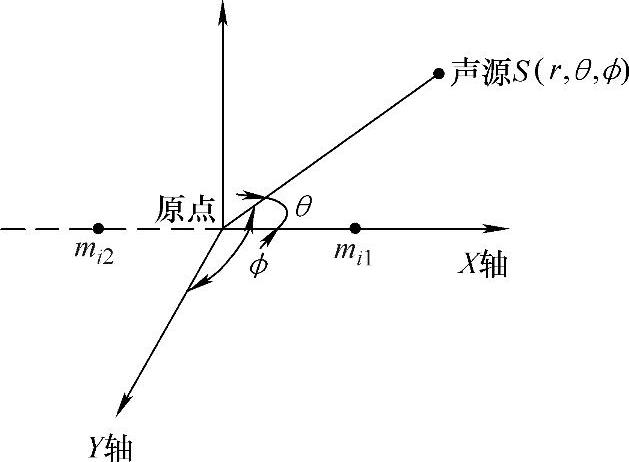
图6-5 声源与麦克风几何位置示意图
以直角坐标的形式表示声源和麦克风位置:
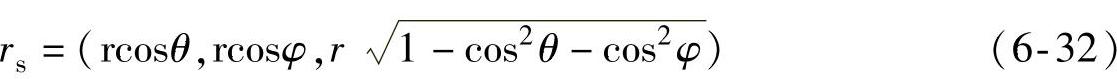
mi1=(|mi1-mi2|/2,0,0),mi2=(-|mi1-mi2|/2,0,0) (6-33)
将式(6-33)代入式(6-31),两边平方可得
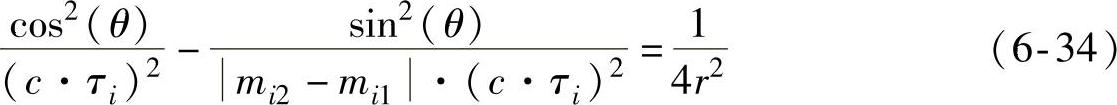
当声源离麦克风比较远时(即r变得很大时,1/4r2趋近于零)。可以用锥面代替双曲面。该锥面的方向角可以由式(6-35)计算:

该替换过程可以由图6-6所示。因此只要求得时延就能近似求得远场声源相对于两麦克风连线中点的方向角。
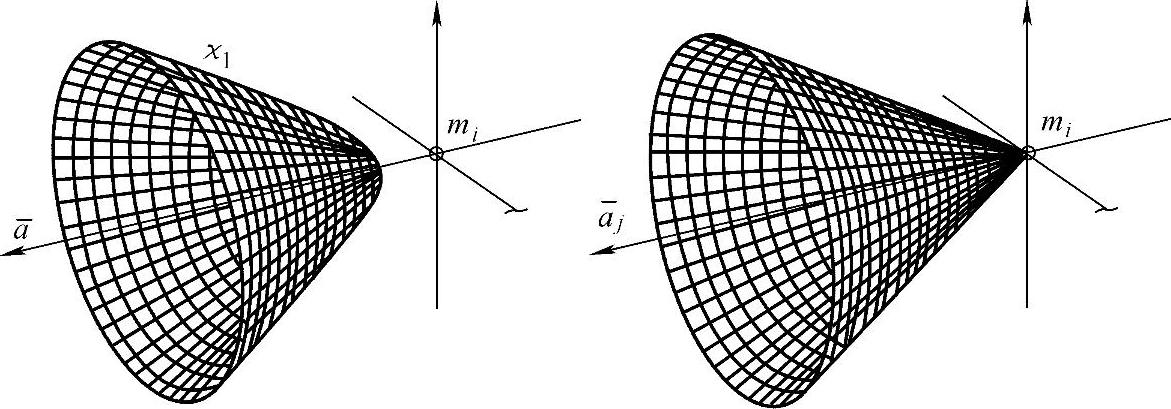
图6-6 声源的双曲面和锥面近似图
(2)搜索定位法 给定N组麦克风的TDOA组合(图6-7),可以利用优化方法来估计真正的声源位置S(图6-8)。S应为可能声源位置的交叉点。然而当麦克风对多于两对时,这个交集往往是一个空集。基于此,一般通过最小化某种误差准则来确定声源位置。下面介绍LS误差准则。
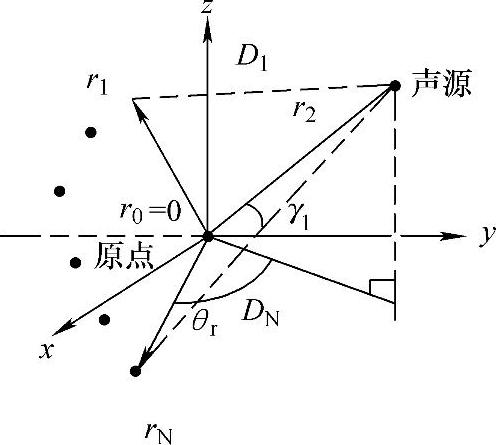
图6-7 声源定位系统变量的空间分布
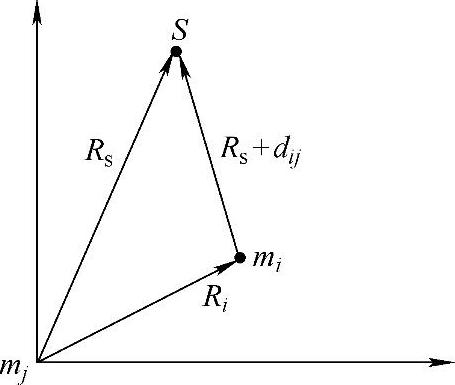
图6-8 麦克风与声源几何关系
假定每对麦克风时延估计τi,受到零均值、方差为var{τi}的加性高斯白噪声污染,那么最大似然位置估计应使得式(6-36)的(LS)误差准则最小,即
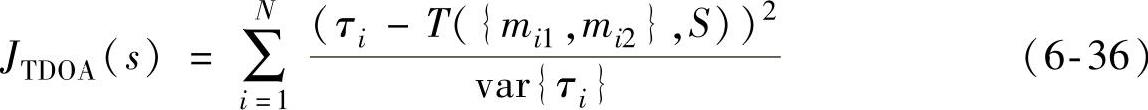
于是可得到估计的声源位置为

1)球形插值法。球形插值法根据多个麦克风对的时延求得一组方程,并在满足最小均方误差准则下解这个方程组。下面给出详细的推导过程。(https://www.xing528.com)
设麦克阵列由N+1个位于ri=(xi,yi,zi)T(i=0,…,N)的麦克风组成。麦克风0(i=0为参考麦克风,坐标原点r0=(0,0,0),声源位于rs=(xs,ys,zs)T,各麦克风和声源到原点的距离分别定义为Ri和Rs。
其中
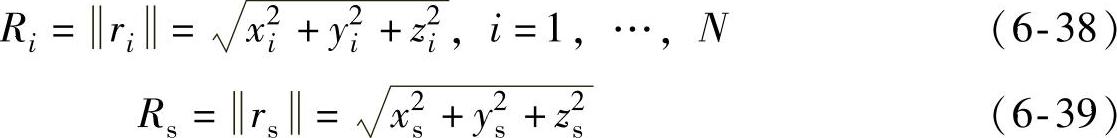
声源与麦克风i的距离为
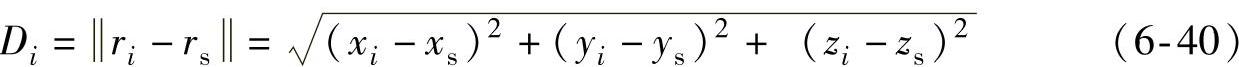
麦克风i与麦克风j的距离差为
dij=Di-Dji,j=0,…,N (6-41)
因为D0=Rs,于是有
Di=di0+Rs (6-42)
将式(6-42)代入(6-40)两边平方得
(di0+Rs)2=D2i=(ri-rs)T(ri-rs)=Ri2-2riTrs+Rs2 (6-43)
将式(6-43)展开得
Ri2-di02-2Rsdi0-2riTrs=0 (6-44)
di0是通过时延估计得到的,其与实际的i号传感器到原点的距离有所偏差,因此式(6-44)需改写为
∈=Ri2-di02-2Rsdi0-2riTrs (6-45)
模型中共有4个传声器,将式(6-45)改写为矩阵形式:
∈=δ-2Rsd-2rsS (6-46)
其中
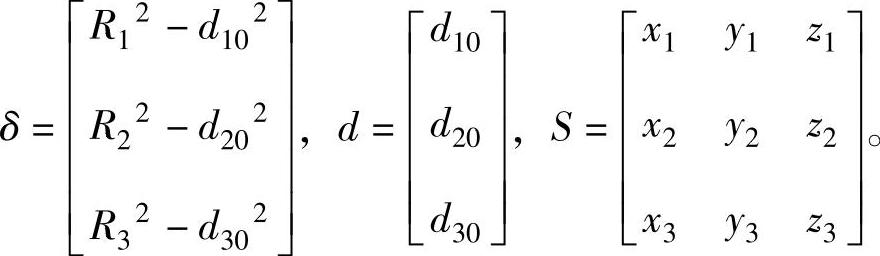
假设给定Rs,当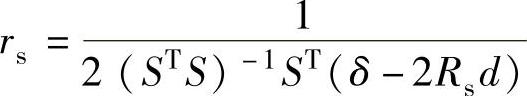 时式(6-45)的均方误差最小。接着将rs的值代入(6-45)反求出Rs。最后将Rs的值代入(6-46)即可求出线性均分最小的rs的估计值,得到精确的声源位置。
时式(6-45)的均方误差最小。接着将rs的值代入(6-45)反求出Rs。最后将Rs的值代入(6-46)即可求出线性均分最小的rs的估计值,得到精确的声源位置。
2)线性插值声源定位法。线性插值声源定位法利用4个麦克风定出2个方向角,由这2个方向角可以确定出一条方向线,而声源就应该在这条方向线上,基本麦克风摆放如图6-9所示。
实现线性插值法需要多组传声器阵列数据,将一组传声器进行移动可以代替多组传声器。一组传声器线性差值法求解原理及阵列布置如图6-10、图6-11所示。
mj1/mj2/mj3/mj4分别是四个垂直且连线平分摆放的传声器,原点为mj。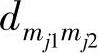 是声源到传声器mj1、mj2的距离差(即时延与声速之积),
是声源到传声器mj1、mj2的距离差(即时延与声速之积),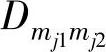 是传声器mj1、mj2间的距离。
是传声器mj1、mj2间的距离。
由空间解析几何可知,声源在角αj、βj确定的唯一一条直线上,而多组传声器阵列所确定的直线交点就是声源的位置,这是定位的理论模型。但在实际情况中,时延值必然会引入误差,这将导致直线不能相交于一点。我们认为若有两条这样不相交的方向线li、lj,可在两条线上分别找到两个点,并使两点之间的距离最短,这两点记为Sij、Sji。根据时延估计的方差可设Sij、Sji的权值为ωij、ωji,通过线性插值公式可求出此时声源坐标:
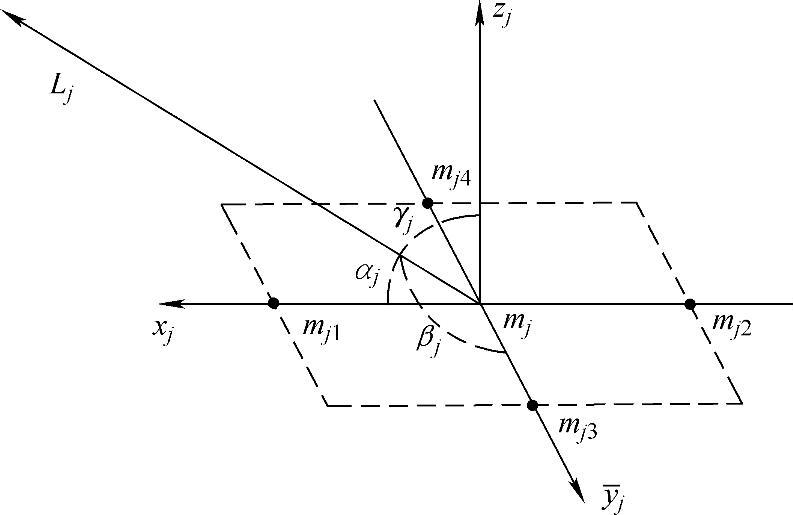
图6-9线性插值法的麦克风摆放结构
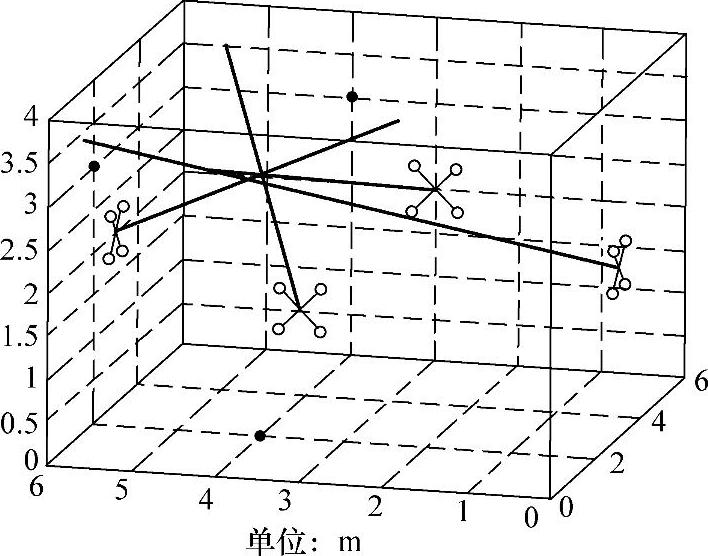
图6-10线性插值法求解原理图
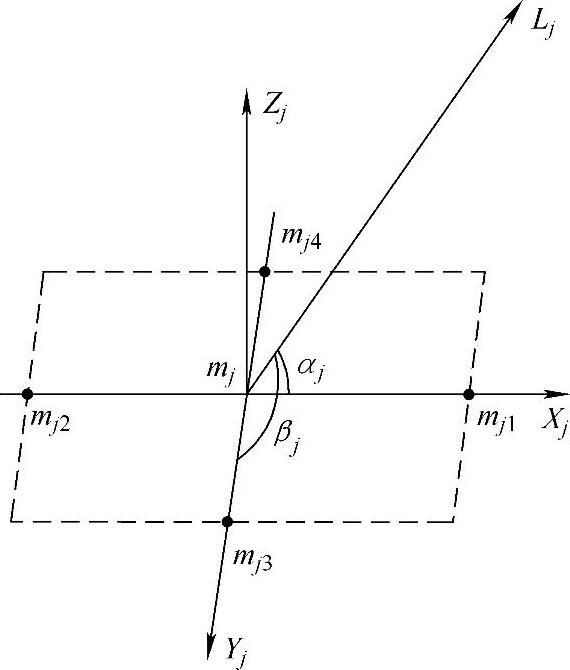
图6-11线性插值法单组阵列布置图
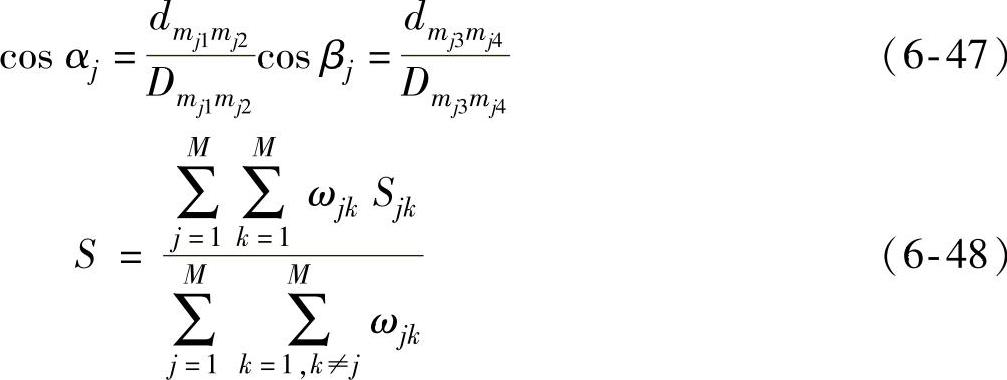
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




