模型预测控制优化

模型预测控制（Model Predictive Control，MPC）是一种基于求解在线最优化控制问题的算法，适用于控制不易建立精确数字模型且比较复杂的工作生产过程。MPC的基本原理如图7.2所示，在当前采样时刻k，以当前时刻的状态作为初始状态，通过系统模型预测在[k，k ＋N]时间段的动态行为；考虑当前和未来的约束并基于性能指标函数，在线求解一个开环的最优控制问题，得到[k，k ＋M]时间段的最优控制输入序列；由于外部干扰和模型不确定性，将最优控制输入序列的第一个分量作用于系统；在下一个采样时刻 k ＋1，以新得到的测量值为初始条件重复上述过程，同时将预测时域N和控制时域M向前推移。由此可以看出，MPC的优化过程不是一次离线进行的，而是采用时间向前滚动式的有限时域优化策略，因此MPC也称为滚动时域控制。

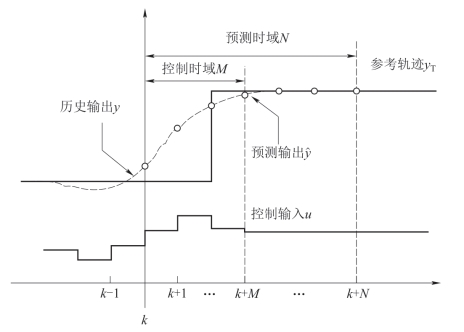
图7.2　模型预测控制原理

MPC目前多采用状态空间模型。考虑如下线性离散时间模型：

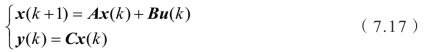(www.xing528.com)

式中，x （k） ∈Rn 为状态变量，u （k） ∈Rm 为控制变量，y （k） ∈Rp 为输出变量。

通过引入以下的开环最优化问题来构造一个滚动时域控制形式：

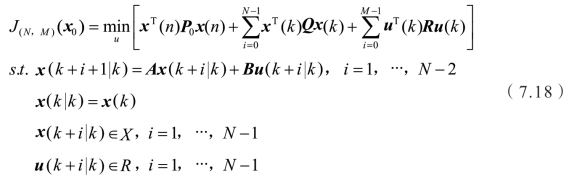
式中，Q，R为权重矩阵，X，R 分别为包含原点在内的系统状态和控制输入的可行解集合。通过求解线性离散时间模型得到最优控制输入序列选取该序列第一个元素作为输入量作用于系统，舍弃其他元素。新的状态 x （k ＋1）作为下一步优化计算的初始值，然后再次计算一个优化解，得到最优控制序列，仅应用第一个元素得到新的状态变量，通过这样不断地反复在线优化，直至完成控制目标。

MPC的优势在于通过考虑时域约束，在线预测被控对象的性能，并通过最优控制来处理多个目标。因此，MPC可以预见和消除前馈和反馈扰动的影响。随着计算机硬件处理能力的快速发展，在要求快速响应的混合动力系统中，MPC已成为颇具吸引力的反馈控制策略。