机电复合传动系统的等效模型

借鉴目前大多数参考文献针对混联式HEV模式切换控制以“忽略功率耦合机构所导致的复杂耦合关系，以单条功率传递通路为主，各动力源的功率和惯量通过线性叠加计算”的研究思路，本节先将机电复合传动系统发动机和两个电机的转矩关系进行解耦，转化为直接作用在离合器主动端与被动端的等效转矩；在保证符合原系统耦合关系的前提下，将复杂的功率耦合机构模型解耦为围绕离合器主、被动端的等效模型，简化了模式切换过程的机理分析，同时也为后文模式切换控制策略的研究和设计提供了更加简洁和有效的途径。

图7.1展示了机电复合传动系统复杂模型及其等效模型的拓扑结构。其中，J1为各部件等效到轴1的转动惯量，J2为各部件等效到轴2的转动惯量，ω1为离合器主动端和轴1的转速，ω2为离合器被动端和轴2的转速，T1为各动力元件等效到轴1的转矩，T2为各动力元件等效到轴2的转矩，Tf1，Tf2分别为轴1和轴2承受来自路面负载的阻力矩。

下面来推导图7.1（a）复杂模型和图7.1（b）等效模型之间转矩和惯量的等效关系。参考基于键合图理论的功率耦合机构模型，以离合器主、被动端为研究主体，根据图7.1（a）推导机电复合传动系统在离合器接合过程中的动力学方程。

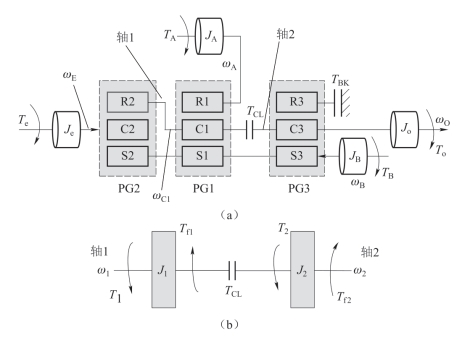
图7.1　机电复合传动系统复杂模型及其等效模型的拓扑结构

（a）复杂模型；（b）等效模型

离合器主动端的动力学方程：

离合器被动端的动力学方程：

式中，行星架C1的转速等于离合器主动端的转速，即 ω1=ωc1；输出轴的转速等于离合器被动端的转速，即 ω2=ωo。

发动机、电机A和电机B的转速变化率为

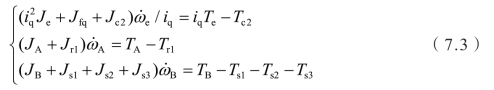
各部件的转速关系式为

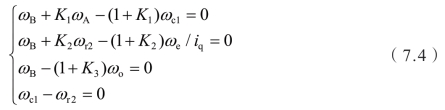
各部件的转矩关系式为

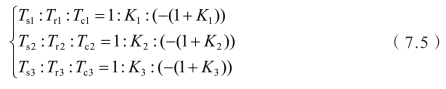
综合公式，推导离合器主动端的转矩关系式为(www.xing528.com)

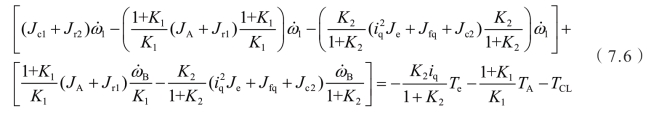
由于行星排内部的惯量相比于发动机惯量和电机惯量较小，可以忽略，所以上式可以简化为

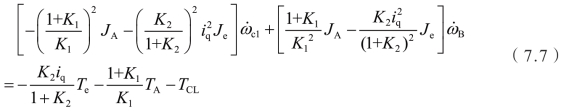
由上面的公式可知

ωB=(1+K3)ωc2

因此可以转化为

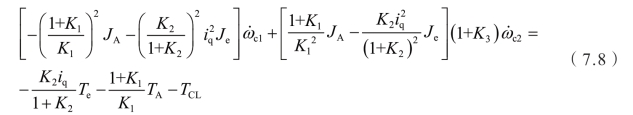
综合以上公式，忽略行星排内部的惯量，推导出离合器被动端的转矩关系式为

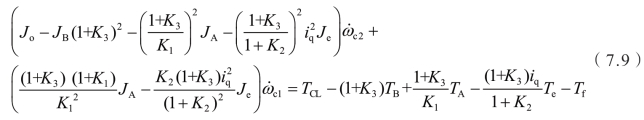
联立上述两式，进一步整理得到

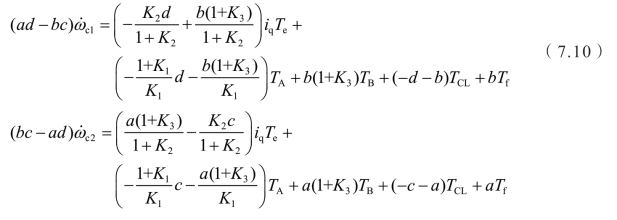
式中，转动惯量系数a、b、c和d的表达式分别为

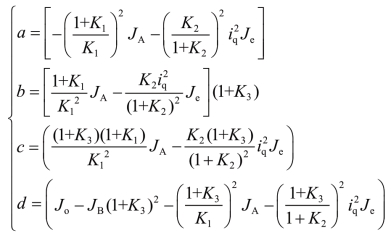
因此，机电复合传动系统在离合器接合过程的动力学方程包含了发动机转矩、电机A转矩、电机B转矩、离合器转矩和负载转矩。可以看出，机电复合传动系统中发动机和两个电机通过与功率耦合机构连接形成了复杂的耦合关系，动力学方程的强耦合特征更加明显。

根据图7.1（b），机电复合传动系统等效模型的动力学方程为

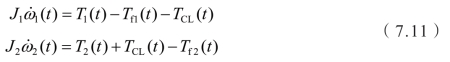
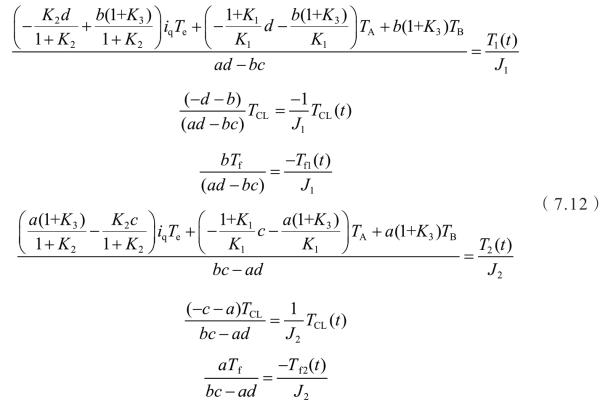
通过对比，图7.1（a）和图7.1（b）的转矩和惯量的等效关系为