空挡转停车发电模式切换稳定性分析

本节针对停车发电模式，采用电机A作为发电机单独给电池组提供电功率，电机B不工作，因此参考前述传动模型和功率耦合机构模型，空挡到停车发电模式切换过程中的动力学方程可表示为

根据功率耦合机构的转速和转矩特性，行星齿轮排的转速关系式为

行星齿轮排的转矩关系式为

这里需要强调，机电复合传动系统在空挡到停车发电模式切换过程中，由于发动机的全程调速特性始终与电机A的转速特性相关联，控制器和执行器对发动机动态特性影响不容忽略，因此需要进一步细化发动机的转矩动态模型。而与空挡到机电驱动模式切换过程相比，电机A和电机B的转速动态特性与发动机转矩无关，因此无须强调发动机的转矩动态特性。

当发动机考虑采用PI控制器的全程调速模式时，其供油齿杆行程百分比可以表示为

式中，ωr为参考发动机转速；ωe为实际发动机转速；Kp和 KI分别代表比例系数和积分系数。参考发动机外特性曲线，同时考虑油门执行器与发动机增压涡轮的迟滞特性，具有全程调速特性的发动机转矩动态方程为

式中，τe为发动机的转矩响应时间常数，这里取值0.3；参数a1，a2根据发动机外特性数据拟合得到，并且满足a1 ＞0，a2 ＜0。

针对电机A模型，将TA转化为

式中，TA_ref为电机A的参考转矩；τA为电机A的转矩响应时间常数，这里取值0.005。

联立以上公式，推导发动机的转速变化率表达式为

推导电机A的转速变化率表达式为

上述两公式是典型的非线性时变系统，理论上很难求得解析解，因此该系统的稳定性可以通过局部线性化并计算雅可比矩阵来分析，将平衡点移动到处

同时忽略高阶无穷小项，得到

式中，

针对非线性时变自治系统（6.37），取状态变量为则系统的雅可比矩阵可以推导为

(www.xing528.com)

在 x （t）=0处的表达式为

分析上式可以发现，含有前述传动模型刚度和阻尼参数的雅可比矩阵第一行和第二行近似线性相关，说明在空挡到停车发电模式切换过程中，机电复合传动系统的稳定性不受前述传动模型中刚度和阻尼参数的影响，可以忽略。由此，在停车发电模式下，可以将机电复合传动系统简化为“发动机-齿轮副-发电机组模型”，如图6.7所示。

基于简化模型，在从空挡到停车发电模式的切换过程中，机电复合传动系统的动力学模型可以表示为

图6.7　发动机-齿轮副-发电机组模型

式中，i代表发动机和发电机之间的齿轮副传动比。同样的，上式是典型的非线性时变系统，理论上很难求得解析解，因此该系统的稳定性可以通过局部线性化并计算雅可比矩阵来分析。将上式的平衡点移动到 ωr处，同时忽略高阶无穷小项，得到

在 x （t）=0处雅可比矩阵的表达式为

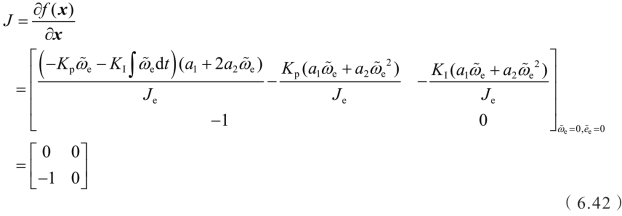
所对应的雅可比矩阵特征值为零，因此该时变非线性系统无法通过局部线性化的方法分析其稳定性。借助中心流形定理，对状态变量进行矩阵变化

然后，构造函数 y=h（x）的表达式为

根据条件约束方程以及边界约束条件，求得系数分别为

最后，基于以上推导，非线性时变系统第一项可以转化为

分析公式（6.46）可以发现，有界，不影响系统的稳定性。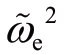与 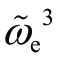项前面的系数符号决定着系统的稳定性。根据发动机及其调速器的物理特性，上述参数需满足

a1 ＞0，a2 ＜0，Kp ＞0，KI＞0

因此为负数，项收敛；项的符号取决于的符号，为保证系统的稳定性，需满足

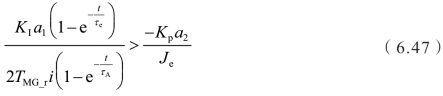
当时间t满足 t →0时

上式是保证由空挡转换为停车发电模式切换过程稳定性的必要条件。否则，机电复合传动系统容易出现失稳。