等效因子对电池SOC轨迹影响的优化策略

引入等效因子的目的是将上一小节中提及的额外需要满足的约束条件嵌入优化成本函数中，从而对发动机工作点进行修正，注意观察式（3.36）的形式，等效因子实际上在ECMS的成本函数中起到类似于一个权重因子的作用，其为ECMS实现过程的一个重要控制参数。

若定义，则可将式（3.36）的第二项表示为

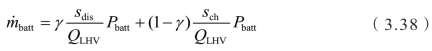
标准ECMS将等效因子设定为常数［112］，显然对于不同的行驶工况，油箱和电池系统之间的平均效率并不相同，无法直接获得一组等效因子值（sch，sdis）能使车辆在任意工况下均获得最佳的控制效果。对于某已知工况，最终车辆的性能指标（燃油消耗）可被看作等效因子的函数，进而利用优化算法求解二维优化问题，获得使该工况燃油消耗最少的最佳等效因子（sc 0h，sd0is）。在文献［19］中，利用 s 0=γsc 0h ＋ （1－γ）sd 0is将上述二维优化问题简化为一维问 题。s0需要利用迭代求解算法来获得，最常用的方法为打靶法（Shooting Algorithm），其具体流程如图3.3所示。

针对某车辆提前将一系列典型行驶工况的最优等效因子s0利用上述流程图中的步骤离线计算获得，在实际应用时根据一系列特征参数识别出与实际行驶过程最接近的典型工况，进而选择对应的s0值，该方法在完整工况信息提前确定的情况下可获得与DP所求得的最优解非常接近的效果［19，113，114］。

以IM240（Inspection & Maintenance Driving Cycle）工况为例，分析不同等效因子值对控制效果的影响，仿真结果如图3.4所示。从结果图中观察可看出，IM240的最佳常数等效因子为2.47，当等效因子取为2.46或2.48时（与最佳等效因子偏差仅为0.01），最终的SOC仍明显地偏离了期望值0.6，而当等效因子取为2.45或2.5时，SOC值已经超出了设计的0.5～0.7这一最佳工作范围。

(www.xing528.com)

图3.3　最佳等效因子求解流程

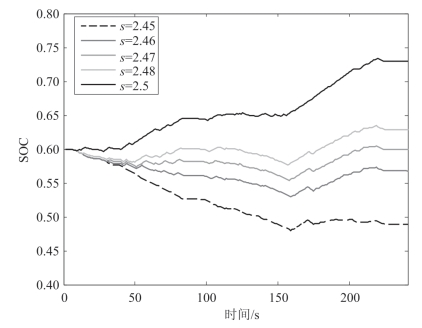
图3.4　不同等效因子值对应的SOC轨迹（IM240工况）

在工况提前获知的前提下，通过离线计算得到的最佳等效常数因子还与初始条件（工况开始时的SOC）有关，图3.5所示为起始SOC为0.4和0.8时的SOC轨迹，仍采用离线计算 SOC（t0）=0.6获得的常数等效因子2.47，可以看出，终点处的SOC既无法到达期望值（0.6），也没有回到初始值（0.4或0.8）。当初始SOC值不等于求解最佳常数等效因子采用的初始的 SOC（t0）时，标准ECMS的控制效果也得不到保证。

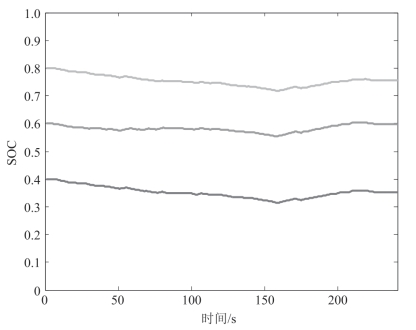
图3.5　相同等效因子、不同初值对应的SOC轨迹（IM240工况）

总体而言，等效燃油消耗最小化策略对于常数等效因子的取值比较敏感，每一个工况均对应了一个最佳常数等效因子，若实际行驶工况偏离了离线计算最佳常数等效因子时所使用的工况，能量管理策略即使仍可使用，但效果将会变差，甚至还可能导致电池SOC超出设计的工作范围。